Активные и индуктивные сопротивления проводов

Введение

IEC 60228:2004 устанавливает требования к номинальному сечению токопроводящих жил электрических кабелей, проводов и шнуров широкого диапазона типов, включая требования к числу и диаметру проволок и значению электрического сопротивления. IЕС 60228:2004 устанавливает требования к конструкции жил только для силовых кабелей и шнуров (см. раздел 1), поэтому содержит только классы жил 1, 2, 5 и 6. В настоящее время в странах СНГ разработано большое количество кабельных изделий с жилами классов 3 и 4, поэтому настоящий стандарт дополнен этими классами и из раздела 1 исключено слово «силовых». Требования к токопроводящим жилам электрических кабелей, проводов и шнуров в настоящем стандарте полностью соответствуют установленным в IEC 60228:2004. При этом в настоящем стандарте расширены требования IEC 60228:2004 на все группы кабельных изделий, также сохранены диапазоны сечений жил по классам; для класса 1 сохранено изготовление жил из алюминия и возможность изготовления многопроволочных жил наряду с однопроволочными. Размеры жил, приведенные в настоящем стандарте, установлены в метрической системе. В настоящее время Канада для указания размеров и параметров жил использует американские системы AWG (American Wire Gauge) и kcmil (kilo circular mils) для больших размеров, как показано ниже. Применение в Канаде этого размерного ряда предписано национальными нормами для электроустановок. В стандартах IEC на кабельные изделия нет кабелей, проводов и шнуров с жилами в системе AWG/kcmil.

AWG	kcmil
Размер жилы	Номинальное сечение жилы, мм	Размер жилы	Номинальное сечение жилы, мм	Размер жилы	Номинальное сечение жилы, мм	Размер жилы	Номинальное сечение жилы, мм
—	—	—	—	250	127	750	380
—	—	—	—	300	152	800	405
20	0,519	4	21,2	350	177	900	456
18	0,823	3	26,7	400	203	1000	507
16	1,31	2	33,6	450	228	1200	608
14	2,08	1	42,4	500	253	1250	633
12	3,31	1/0	53,5	550	279	1500	760
10	5,26	2/0	67,4	600	304	1750	887
8	8,37	3/0	85,0	650	329	2000	1010
6	13,3	4/0	107	700	355	—	—

Варианты измерения

Индуктивность катушки в физике определяется путём выполнения вычислений. Однако эту величину можно не только рассчитать, но и измерить. Делается это при помощи прямого или косвенного метода.

Прямой метод

Для измерения индуктивности катушки этим методом необходимо использовать специальные мостовые или прямопоказывающие устройства. С их помощью можно получить максимально точные данные, которые помогут выбрать требуемую катушку для схемы.

Порядок проведения измерений включает в себя следующие этапы:

1. К прямопоказывающему приспособлению подключают катушку.
2. После этого постепенно изменяют диапазоны измерений. Это делается до тех пор, пока получаемый результат не будет находиться примерно в середине интервала.
3. Полученный результат фиксируют и высчитывают с учётом цены деления прибора, а также коэффициента, соответствующего положению переключателя.

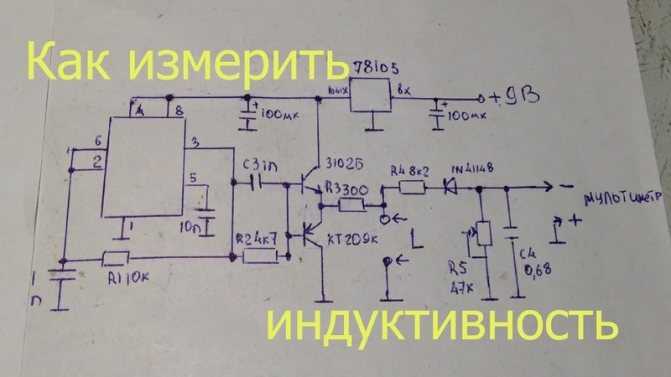
Измерение выполняют путём проведения таких действий:

1. Включённый мостовой прибор подсоединяют к катушке, индуктивность которой необходимо определить.
2. Аналогично прямопоказывающему устройству проводят переключение интервалов измерений.
3. После каждого такого действия ручку регулятора балансировки моста поочерёдно перемещают в одно и другое предельное положение.
4. Как только удалось определить диапазон, в котором мост будет сбалансирован, можно выполнять дальнейшие действия.
5. На следующем этапе измерений выполняется постепенное перемещение стрелочного индикатора.
6. После того как в динамике прибора исчезнет звук, необходимо зафиксировать показатели.
7. Затем их рассчитывают в соответствии с ценой деления шкалы и предусмотренным коэффициентом.

Вам это будет интересно Особенности измерения в люменах и ваттах

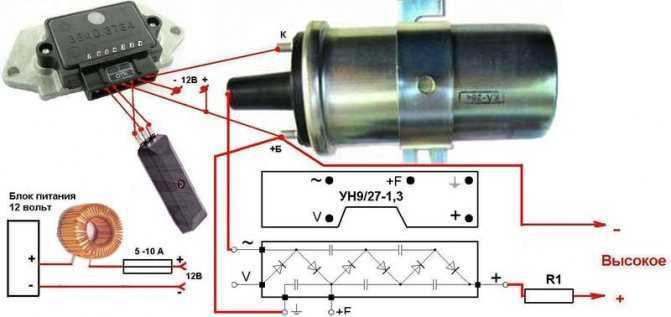
Косвенное определение

Для того чтобы измерить коэффициент самоиндукции, необходимо провести несколько подготовительных мероприятий. В первую очередь нужно собрать измерительную цепь по стандартной схеме, а также подготовить все необходимые приспособления (генератор синусоидального напряжения, частотомер, а также миллиамперметр и вольтметр, рассчитанные на переменный ток).

Порядок определения параметра:

1. К выходу генератора параллельно подключают вольтметр. Он должен быть переключён в режим, при котором верхнее предельное значение будет соответствовать напряжению в 3−5 вольт.
2. Аналогично подсоединяют и частотомер.
3. Отдельно собирают вторую цепь. В ней последовательно соединяют миллиамперметр и катушку, индуктивность которой нужно определить.
4. Затем обе цепи подключают параллельно друг к другу.
5. Подключённый генератор устанавливают в режим выработки синусоидального напряжения.
6. Путём изменения частоты добиваются такой работы приборов, при которой вольтметр будет показывать примерно 2 вольта. При этом сила тока на миллиамперметре будет постепенно уменьшаться.
7. После этого ручку частотомера перемещают в положение, соответствующее частоте измерений.
8. Как только эти действия будут выполнены, можно фиксировать значения.

Полученные данные переводятся в СИ, а затем выполняются все необходимые расчёты. Первым делом определяется индуктивное сопротивление. Для этого значения приборов подставляются в следующую зависимость: X=U/I, где U — напряжение, а I — сила тока. Результат расчётов будет выражен в омах.

После этого вычисляется индуктивность по формуле L=X/2 πF. В ней используются такие условные обозначения:

• X — индуктивное сопротивление;
• π — математическая постоянная (примерно 3,14);
• F — частота в герцах, при которой проводились измерения.

Индуктивность — это важный физический параметр, позволяющий определить магнитные свойства электроцепи. При точном его измерении и правильном проведении предусмотренных расчётов можно получить достоверные данные, которые понадобятся при выборе катушки.

Доступна Windows-версия программы расчёта потерь напряжения

Пояснения к расчёту

Расчёт потерь линейного (между фазами) напряжения в кабеле при трёхфазном переменном токе производится по формулам:

или (если известен ток)

где

Расчёт потерь фазного (между фазой и нулевым проводом) напряжения в кабеле производится по формулам:

или (если известен ток)

где

Для расчёта потерь линейного напряжения U=380 В; 3 фазы.

Для расчёта потерь фазного напряжения U=220 В; 1 фаза.

P — активная мощность передаваемая по линии, Вт; Q — реактивная мощность передаваемая по линии, ВАр; R — удельное активное сопротивление кабельной линии, Ом/м; X — удельное индуктивное сопротивление кабельной линии, Ом/м; L — длина кабельной линии, м; Uл — линейное напряжение сети, В; Uф — фазное напряжение сети, В.

Пожелания, замечания, рекомендации по улучшению раздела расчётов на нашем сайте просьба присылать по электронной почте Разрешается копирование java-скриптов при условии ссылки на источник.

ВСЕ РАСЧЁТЫ

Электрические провода и кабели

Электрические характеристики силовых кабелей

Электрическое сопротивление токопроводящей жилы постоянному току при, Ом/км, температуре Т, °С

 

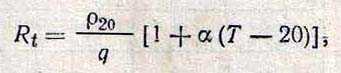
где q — номинальное сечение жилы, мм2; ρ₂₀— удельное сопротивление при 20°С, нОм*м; а— температурный    коэффициент    сопротивления,
равный для меди и алюминия приблизительно 0,004 °С-1.

₂₀22
2

Таблица 1. Значение коэффициента возрастания сопротивления при переменном токе для медных жил

Сечение жилы, мм2	Трехжильные кабели с поясной изоляцией	Три одножильных кабеля, расположенных вплотную по вершинам треугольника
150	1,01	1,006
185	1,02	1,008
240	1,035	1,0105
300	1,052	1,025
400	1,095	1,05
500	1,15	1,08
625	—	1,125
800	—	1,2
1000	—	1,29

₁Таблица 2. Коэффициент L₁ для расчета индуктивности кабелей

Число проволок в жиле	Одножильные кабели	Трехжильные кабели
3	0,075	0,0766
7	0,0638	0,065
10	0,0556	0,0567
37	0,0531	0,0543
61	0,0525	0,0535
Более 61	0,0502	0,0513

 
 
Таблица 3. Активное и индуктивное сопротивление трехжильных кабелей с поясной изоляцией

Сечение, мм2	Активное сопротивление, Ом/км, при 20 oС	Индуктивное сопротивление Ом/км, при напряжении
	Алюминий	Медь	6 кВ	10 кВ
1,5	19,62	11,95	—	—
2,5	11,75	7,17	—	—
4	7,85	4,5	—	—
6	4,9	3	—	—
10	2,94	1,79	0,11	0,122
16	1,84	1,12	0,102	0,113
25	1,17	0,716	0,091	0,099
35	0,84	0,514	0,087	0,095
50	0,589	0,359	0,083	0,09
70	0,42	0,256	0,08	0,086
95	0,31	0,189	0,078	0,083
120	0,245	0,15	0,076	0,081
150	0,196	0,12	0,074	0,079
185	0,159	0,097	0,073	0,077
240	0,125	0,075	0,071	0,075

 
 

 
-12_rr 

_pном 

_1p2p12 

 

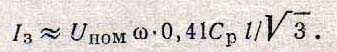
Таблица 4. Рабочая емкость С_р, мкФ/км, трехжильных кабелей с поясной изоляцией в трехфазных цепях с симетричным напряжением

Напряжение, кВ	Сечение жилы, мм2
10	16	25	35	50	70	95	120	150	185	240
1	0,35	0,4	0,5	0,53	0,63	0,72	0,77	0,81	0,86	0,87	—
6	0,2	0,23	0,28	0,31	0,36	0,4	0,42	0,46	0,51	0,53	0,58
10	—	—	0,26	0,27	0,29	0,31	0,35	0,37	0,44	0,45	0,46

 
 
Таблица 5. Емкость, мкФ/км, одножильных кабелей и фазы трехжильных кабелей с отдельно совинцованными жилами с бумажной пропитанной изоляцией

Напряжение, кВ	Сечение жилы, мм2
25	35	50	70	95	120	150	185	240	300	400
20	0,17	0,19	0,21	0,24	0,26	0,32	0,35	0,38	0,42	0,46	0,51
35	—	—	—	0,18	0,2	0,24	0,26	0,28	0,31	0,33	—

 
 
Таблица 6. Емкость фазы маслонаполненных кабелей

Тип кабеля	Напряжение, кВ	Сечение, мм2	Толщина изоляции, мм	Емкость, мкФ/км
Маслонаполненный с центральным маслопроводящим каналом	110	150	11	0,25
270	10	0,33
625	9,6	0,45
220	350	20	0,22
500	18,8	0,27
625	18	0,28
Маслонаполненный для затягивания в стальной трубопровод	110	270	10,7	0,3
425	10	0,37
700	9,6	0,46
220	300	20,7	0,2
550	18,1	0,28
700	17,5	0,29
380525	550	26	0,21
625	30	0,19

Кабели
ЛЭП
ТОЭЭ
ТЭЦ
РиЭКТ
Метрология
Реальная физика
Сверхпроводимость
Удельное сопротивление металлов

Знаете ли Вы, что, как и всякая идолопоклонническая религия, релятивизм представляет собой инструмент идеологического подчинения одних людей другим с помощью абсолютно бессовестной манипуляции их психикой для достижения интересов определенных групп людей, стоящих у руля этой воровской машины? Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМАРыцари теории эфира

10.11.2021 — 12:37: ПЕРСОНАЛИИ — Personalias -> — Карим_Хайдаров.10.11.2021 — 12:36: СОВЕСТЬ — Conscience -> — Карим_Хайдаров.10.11.2021 — 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ — Upbringing, Inlightening, Education -> — Карим_Хайдаров.10.11.2021 — 12:35: ЭКОЛОГИЯ — Ecology -> — Карим_Хайдаров.10.11.2021 — 12:34: ВОЙНА, ПОЛИТИКА И НАУКА — War, Politics and Science -> — Карим_Хайдаров.10.11.2021 — 12:34: ВОЙНА, ПОЛИТИКА И НАУКА — War, Politics and Science -> — Карим_Хайдаров.10.11.2021 — 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ — Upbringing, Inlightening, Education -> — Карим_Хайдаров.10.11.2021 — 09:18: НОВЫЕ ТЕХНОЛОГИИ — New Technologies -> — Карим_Хайдаров.10.11.2021 — 09:18: ЭКОЛОГИЯ — Ecology -> — Карим_Хайдаров.10.11.2021 — 09:16: ЭКОЛОГИЯ — Ecology -> — Карим_Хайдаров.10.11.2021 — 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ — Upbringing, Inlightening, Education -> — Карим_Хайдаров.10.11.2021 — 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ — Upbringing, Inlightening, Education -> — Карим_Хайдаров.

Емкость в цепи переменного тока

X_C =1/ ωc  

При включении емкости под переменное напряжение во время t=0, конденсатор полностью разряжен, напряжение на конденсаторе равно 0, и он начинает заряжаться. Поэтому мгновенно появляется ток зарядки. По мере зарядки конденсатора на нем начинает расти напряжение, которое тормозит процесс зарядки, а значит, ток зарядки начинает уменьшаться.

   

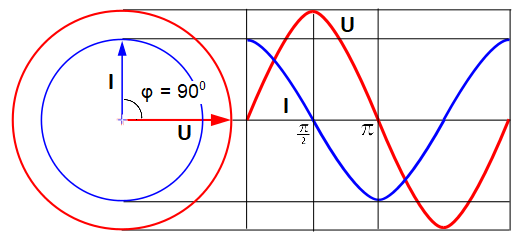
Когда U на конденсаторе достигает максимума, это значит, что оно достигло максимума напряжения источника, зарядка продолжаться не может, поэтому ток становится равным 0.

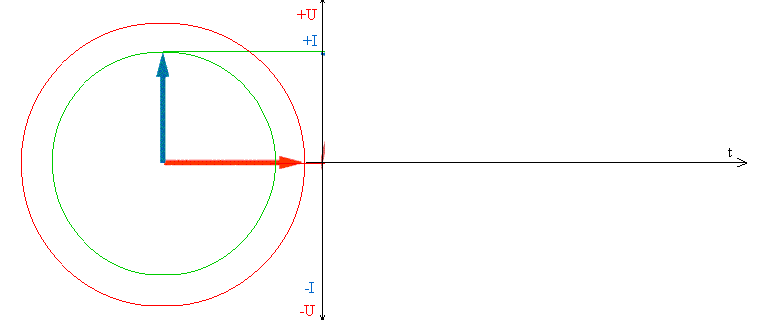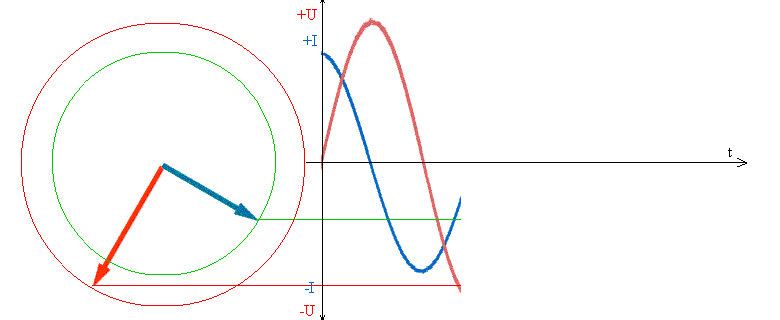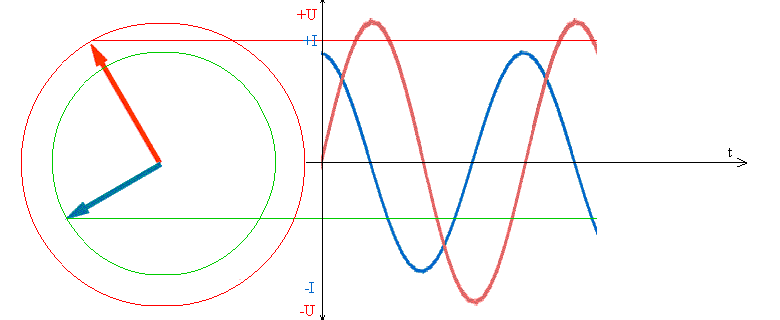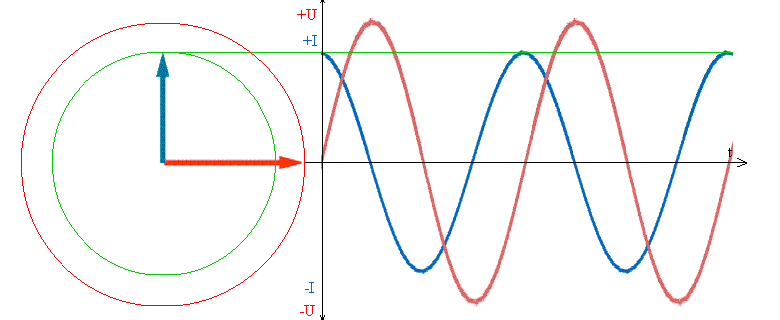
Синусоида тока (синяя) каждый раз пресекает ноль на π/2 раньше, чем (красная) синусоида напряжения.

То есть, максимальному напряжению на емкости соответствует ток, равный 0, а это значит, что ток на емкости С впереди напряжения на 90° или π/2

Что влияет на сопротивление медного провода

Электрический импеданс медного кабеля зависит от нескольких факторов:

• Удельного сопротивления;
• Площади сечения проволоки;
• Длины провода;
• Внешней температуры.

Последним пунктом можно пренебречь в условиях бытового использования кабеля. Заметное изменение импеданса происходит при температурах более 100°C.

Зависимость сопротивления

Удельное сопротивление в системе СИ обозначается буквой ρ. Оно определяется, как величина сопротивления проводника, имеющего сечение 1 м2 и длину 1 м, измеряется в Ом ∙ м2. Такая размерность неудобна в электротехнических расчетах, поэтому часто используется единица измерения Ом ∙ мм2.

Вам это будет интересно Особенности расчета мощности по току и напряжению

Важно! Данный параметр является характеристикой вещества — меди. Он не зависит от формы или площади сечения. Чистота меди, наличие примесей, метод изготовления проволоки, температура проводника — факторы, влияющие на удельное сопротивление

Чистота меди, наличие примесей, метод изготовления проволоки, температура проводника — факторы, влияющие на удельное сопротивление.

Зависимость параметра от температуры описывается следующей формулой: ρt= ρ20. Здесь ρ20— удельное сопротивление меди при 20°C, α— эмпирически найденный коэффициент, от 0°Cдо 100°C для меди имеет значение, равное 0,004 °C-1, t — температура проводника.

Ниже приведена таблица значений ρ для разных металлов при температуре 20°C.

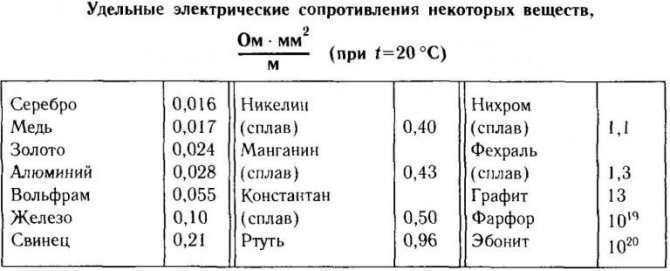
Таблица удельного сопротивления

Согласно таблице, медь имеет низкое удельное сопротивление, ниже только у серебра. Это обуславливает хорошую проводимость металла.

Чем толще провод, тем меньше его резистентность. Зависимость R проводника от сечения называется «обратно пропорциональной».

Важно! При увеличении поперечной площади кабеля, электронам легче проходить сквозь кристаллическую решетку. Поэтому, при увеличении нагрузки и возрастании плотности тока, следует увеличить площадь сечения. Увеличение длины медного кабеля влечет рост его резистентности

Импеданс прямо пропорционален протяженности провода. Чем длиннее проводник, тем больше атомов встречаются на пути свободных электронов

Увеличение длины медного кабеля влечет рост его резистентности. Импеданс прямо пропорционален протяженности провода. Чем длиннее проводник, тем больше атомов встречаются на пути свободных электронов.

Выводы

Последним элементом, влияющим на резистентность меди, является температура среды. Чем она выше, тем большую амплитуду движения имеют атомы кристаллической решетки. Тем самым, они создают дополнительное препятствие для электронов, участвующих в направленном движении.

Важно! Если понизить температуру до абсолютного нуля, имеющего значение 0° Kили -273°C, то будет наблюдаться обратный эффект — явление сверхпроводимости. В этом состоянии вещество имеет нулевое сопротивление. Температурная корреляция

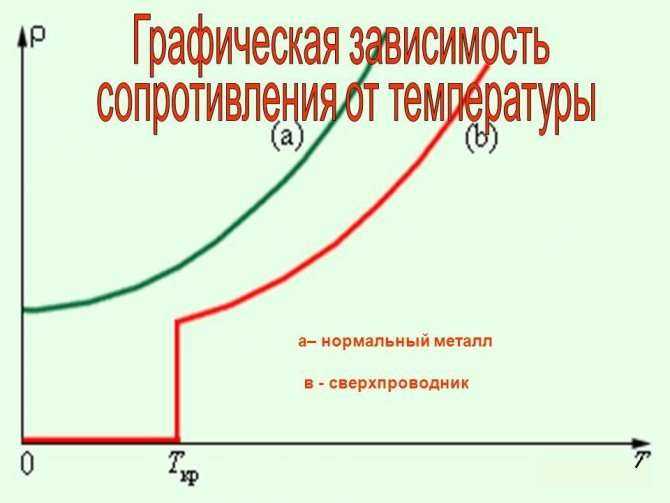
Температурная корреляция

Формулировка для полной цепи

Трактовка для полной цепи будет несколько иной, чем для участка, поскольку в законе, составленном Омом, еще учитывает параметр «r», это сопротивление источника ЭДС. На рисунке ниже проиллюстрирована подобная схема.

Схема с подключенным с источником

Учитывая «r» ЭДС, формула предстанет в следующем виде:

Заметим, если «R» сделать равным 0, то появляется возможность рассчитать «I», возникающий во время короткого замыкания.

Напряжение будет меньше ЭДС, определить его можно по формуле:

Собственно, падение напряжения характеризуется параметром «I*r». Это свойство характерно многим гальваническим источникам питания.

Компенсация реактивной мощности

С помощью электрических сетей осуществляется передача электроэнергии на значительные расстояния. В большинстве случаев она используется для питания электродвигателей, имеющих высокое индуктивное сопротивление и большое количество резистивных элементов. К потребителям поступает полная мощность, которая делится на активную и реактивную. В первом случае с помощью активной мощности совершается полезная работа, а во втором – происходит нагрев трансформаторных обмоток и электродвигателей.

Под действием реактивной составляющей, возникающей на индуктивных сопротивлениях, существенно понижается качество электроэнергии. Противостоять ее вредному воздействию помогает комплекс мероприятий по компенсации с использованием конденсаторных батарей. За счет емкостного сопротивления удается понизить косинус угла φ.

Компенсирующие устройства применяются на подстанциях, от которых электричество поступает к проблемным потребителям. Этот способ дает положительные результаты не только в промышленности, но и на бытовых объектах, снижая нагрузку на оборудование.

Активное и реактивное сопротивление — сопротивлением в электротехнике называется величина, которая характеризует противодействие части цепи электрическому току. Это сопротивление образовано путем изменения электрической энергии в другие типы энергии. В сетях переменного тока имеется необратимое изменение энергии и передача энергии между участниками электрической цепи.

При необратимом изменении электроэнергии компонента цепи в другие типы энергии, сопротивление элемента является активным. При осуществлении обменного процесса электроэнергией между компонентом цепи и источником, то сопротивление реактивное.

В электрической плите электроэнергия необратимо преобразуется в тепло, вследствие этого электроплита имеет активное сопротивление, так же как и элементы, преобразующие электричество в свет, механическое движение и т.д.

В индуктивной обмотке переменный ток образует магнитное поле. Под воздействием переменного тока в обмотке образуется ЭДС самоиндукции, которая направлена навстречу току при его увеличении, и по ходу тока при его уменьшении. Поэтому, ЭДС оказывает противоположное действие изменению тока, создавая индуктивное сопротивление катушки.

С помощью ЭДС самоиндукции осуществляется возвращение энергии магнитного поля обмотки в электрическую цепь. В итоге обмотка индуктивности и источник питания производят обмен энергией. Это можно сравнить с маятником, который при колебаниях преобразует потенциальную и кинетическую энергию. Отсюда следует, что сопротивление индуктивной катушки имеет реактивное сопротивление.

Самоиндукция не образуется в цепи постоянного тока, и индуктивное сопротивление отсутствует. В цепи емкости и источника переменного тока изменяется заряд, значит между емкостью и источником тока протекает переменный ток. При полном заряде конденсатора его энергия наибольшая.

В цепи напряжение емкости создает противодействие течению тока своим сопротивлением, и называется реактивным. Между конденсатором и источником происходит обмен энергией.

После полной зарядки емкости постоянным током напряжение его поля выравнивает напряжение источника, поэтому ток равен нулю.

Конденсатор и катушка в цепи переменного тока работают некоторое время в качестве потребителя энергии, когда накапливают заряд. И также работают в качестве генератора при возвращении энергии обратно в цепь.

Особенности активного сопротивления

Сопротивление в электротехнике является важнейшим параметром, с помощью которого какая-то часть электрической цепи оказывает противодействие проходящему по ней току. Образованию данной величины способствуют изменения электроэнергии и ее переход в другие виды энергетических состояний.

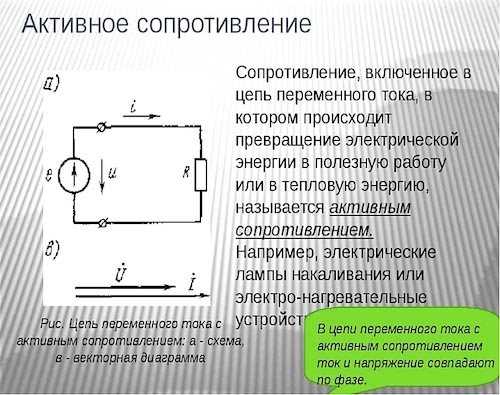
Подобное явление характерно лишь для переменного тока, под действием которого образуются активные и реактивные сопротивления кабелей. Этот процесс представляет собой необратимые изменения энергии или передачу и распределение ее между отдельными элементами цепи. Если изменения электроэнергии принимают необратимый характер, то такое сопротивление будет активным, а если имеют место обменные процессы, оно становится реактивным. Например, электрическая плита выделяет тепло, которое обратно в электрическую энергию уже не превращается.

Данное явление в полной мере затрагивает любые виды провода и кабеля. При одинаковых условиях, они будут по-разному сопротивляться прохождению постоянного и переменного тока. Подобная ситуация возникает из-за неравномерного распределения переменного тока по сечению проводника, в результате чего образуется так называемый поверхностный эффект.

Зачем нужно измерять силу тока

Силу тока в проводнике или на участке электрической цепи измеряют для того, чтобы иметь понятие о характеристиках данного проводника или цепи. Так как сила тока – один из основных параметров электричества, он неразрывно связан с другими значениями по типу напряжения и сопротивления. Более того, как уже стало понятно, три этих величины могут пропорционально определять друг друга.

Расчеты силы электротока делаются в разных случаях:

• При прокладке электрических сетей.
• При создании приборов.
• В образовательных целях.
• При выборе подходящих деталей для совершения тех или иных действий.

Что такое электрический импеданс

В цепях постоянного тока активное сопротивление R играет важную роль. Что касается цепей синусоидального переменного тока, то здесь не обойтись одним лишь активным сопротивлением. Ведь если в цепях постоянного тока емкости и индуктивности заметны только при переходных процессах, то в цепях переменного тока данные компоненты проявляют себя гораздо более значительно.

Поэтому для адекватного расчета цепей переменного тока вводится термин «электрический импеданс» — Z или комплексное (полное) сопротивление двухполюсника гармоническому сигналу. Иногда говорят просто «импеданс», отбрасывая слово «электрический».

Представление об импедансе позволяет применять закон Ома к участкам цепей переменного синусоидального тока. Проявление двухполюсником (нагрузкой) индуктивной составляющей приводит к отставанию тока от напряжения на данной частоте, а проявление емкостной составляющей — к отставанию напряжения от тока. Активная же составляющая не вызывает задержки между током и напряжением, проявляя себя по сути так же, как и в цепи постоянного тока.

Составляющая импеданса, содержащая емкостной и индуктивный компоненты, называется реактивной составляющей X. Графически активную составляющую R импеданса можно отложить по оси оX, а реактивную — по оси оY, тогда импеданс в целом представится в форме комплексного числа, где j-мнимая единица (мнимая единица в квадрате равна минус 1).

В данном случае наглядно видно, что реактивная составляющая X может быть разложена на емкостную и индуктивную составляющие, которые имеют противоположное направление, то есть оказывают противоположное влияние на фазу тока: при преобладании индуктивной составляющей, импеданс цепи окажется в целом положительным, то есть в цепи ток будет отставать от напряжения, если же станет преобладать емкостной компонент, то напряжение будет отставать от тока.

Схематически этот двухполюсник в приведенном виде изображается так:

Принципиально любая схема линейного двухполюсника может быть приведена к аналогичному виду. Здесь можно определить активную составляющую R, которая от частоты тока не зависит, и реактивную составляющую X, включающую в себя емкостную и индуктивную составляющие.

Из графической модели, где сопротивления представлены векторами, ясно, что модуль импеданса для заданной частоты синусоидального тока вычисляется как длина вектора, представляющего собой сумму векторов X и R. Измеряется импеданс в Омах.

Практически в описаниях цепей синусоидального переменного тока с точки зрения импеданса, можно встретить такие термины, как «активно-индуктивный характер нагрузки» или «активно-емкостная нагрузка» или «чисто активная нагрузка». Имеется ввиду следующее:

Если в цепи преобладает влияние индуктивности L, значит реактивная составляющая X положительна, при этом активная составляющая R мала — это индуктивная нагрузка. Пример индуктивной нагрузки — катушка индуктивности.

Если в цепи преобладает влияние емкости C, значит реактивная составляющая X отрицательна, при этом активная составляющая R мала — это емкостная нагрузка. Пример емкостной нагрузки — конденсатор.

Если в цепи преобладает активное сопротивление R, при этом реактивная составляющая X мала — это активная нагрузка. Пример активной нагрузки — лампа накаливания.

Если в цепи активная составляющая R значительна, но индуктивная составляющая преобладает над емкостной, то есть реактивная составляющая X положительна, нагрузку называют активно-индуктивной. Пример активно-индуктивной нагрузки — асинхронный двигатель.

Если в цепи активная R составляющая значительна, при этом емкостная составляющая преобладает над индуктивной, то есть реактивная составляющая X отрицательна, нагрузку называют активно-емкостной. Пример активно-емкостной нагрузки — блок питания люминесцентной лампы.

Телеграмм канал для тех, кто каждый день хочет узнавать новое и интересное: Школа для электрика

Измерение

Из приведенной выше формулы ясно, что для вычисления R достаточно измерить напряжение на концах проводника и силы тока в нем, и затем разделить одну величину на другую.

Обычно вместо вольтметра и амперметра для этой цели используют специальные приборы — омметры и мегаомметры. Они автоматически делят напряжение на силу тока (цифровые) либо имеют шкалу, проградуированную в омах (аналоговые).

Мегаомметры применяют для измерения сопротивления изоляции, имеющего большое значение — в несколько мегаом (МОм). Сопротивление изоляции нормируется и нуждается в периодическом контроле, — от него зависят безопасность эксплуатации электросети и вероятность аварий.

R электросети также нормируется. При некачественно выполненных электрических соединениях, на этапе монтажа оно может оказаться слишком высоким, что приведет к неоправданным потерям и перегреву проводников с последующим воспламенением изоляции. Чтобы удостовериться в правильности монтажа, осуществляют замер сопротивления петли фаза-ноль.

Для этого можно воспользоваться амперметром, вольтметром и специально подобранным резистором (подбирается так, чтобы протекающий ток имел силу порядка 20 А), но лучше воспользоваться специальным прибором, в котором все это уже есть.

Достаточно включить устройство в розетку и нажать кнопку, как оно самостоятельно произведет все измерения и вычислит результат. Часто в рекламных проспектах такие приборы называют «измерителями тока короткого замыкания», но это неверно: они не определяют ток КЗ, а лишь вычисляют его на основании полученного сопротивления петли фаза-ноль.

Чтобы минимизировать R линии, провода соединяют одним из следующих способов:

• пайкой;
• гильзами под опрессовку (обжимаются пресс-клещами);
• посредством клемм;
• путем установки на концы проводов специальных наконечников.

Соединение проводов простой скруткой может дорого обойтись владельцу дома.

Определение активных и индуктивных сопротивлений проводов

Доброго времени суток. В данной статье речь пойдет о расчете активных и индуктивных сопротивлений для воздушных и кабельных линий из цветных металлов, таких как медь и алюминий. Данные расчеты обычно приходится выполнять, когда нужно выполнить расчет токов короткого замыкания в распределительных сетях.

Определение активного сопротивления проводов

Активное сопротивлении проводов проще всего определять по справочным данным, составленным на основании ГОСТ 839-80 – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. Данные таблицы вы сможете найти непосредственно в самом ГОСТ, приведу лишь не которые.

Пользоваться всеми известными формулами по определению активного сопротивления — не рекомендуется ,связано это с тем, что действительное сечение отличается от номинального сечения, провода выпускались в разное время, по разным ГОСТ и ТУ и величины удельной проводимости (ρ) и удельного сопротивления (γ) у них разные:

где:

• γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
• s – номинальное сечение провода(кабеля),мм2;
• l – длина линии, м;
• ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см. таблицу 1.14 .

Активные сопротивления стальных проводов математическому расчету не поддаются. Поэтому рекомендую для определения активного сопротивления использовать приложения П23 – П25 .

Определение индуктивного сопротивления проводов

Индуктивное сопротивление воздушных линий для стандартной частоты f = 50 Гц и относительной магнитной проницаемости для цветных металлов µ = 1, определяется по известной всем формуле :

где:

• Dср. – среднее геометрическое расстояние между проводами, мм;
• dр – расчетный диаметр провода (мм2), определяется по ГОСТ 839-80, таблицы 1 -4;

Среднее геометрическое расстояние между проводами определяется по формуле :

где:

• D1-2 — расстояние между проводами первой и второй фазы;
• D2-3 — расстояние между проводами второй и третей фазой;
• D1-3 — расстояние между первой и третей фазой.

Данные значения определяются по чертежам опор линий электропередачи.

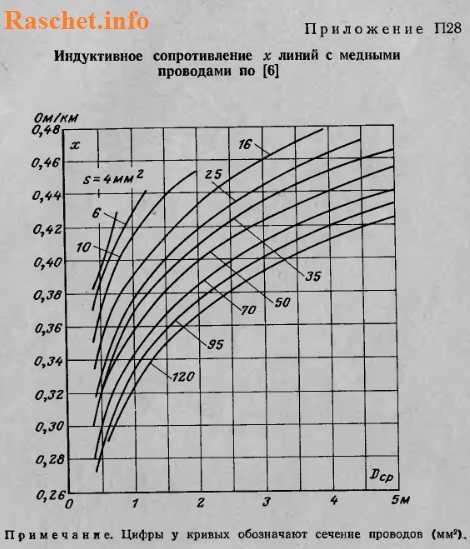
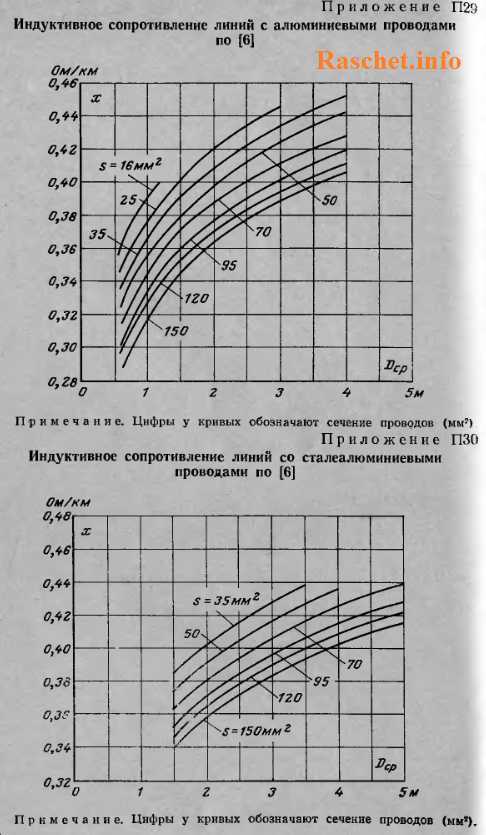
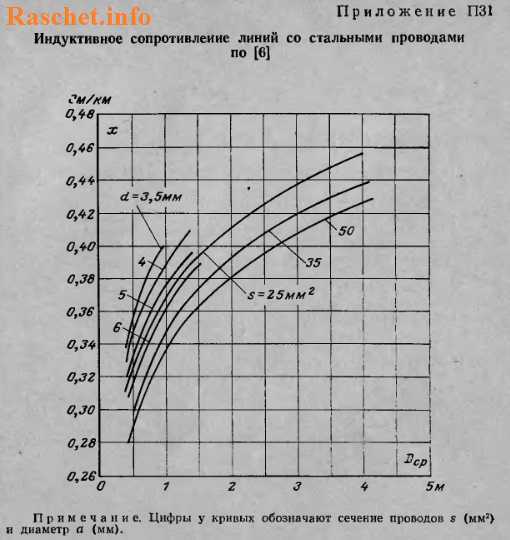
Для упрощения расчетов индуктивного сопротивления проводов рекомендуется использовать приложения П28-П31 , предварительно определив значение Dср.

Если же нужно выполнить приближенный расчет, то можно использовать в расчетах средние значения сопротивлений:

• для линий 0,4 – 10 кВ х = 0,3 Ом/км;
• для линий 35 кВ х = 0,4 Ом/км;
• для стальных проводов использовать приложение П6 ;

Индуктивное сопротивление кабелей рассчитать довольно сложно, из-за различной их конструкции. Поэтому активные и индуктивные сопротивления кабелей рекомендуется принимать по справочникам, приложение П7 .

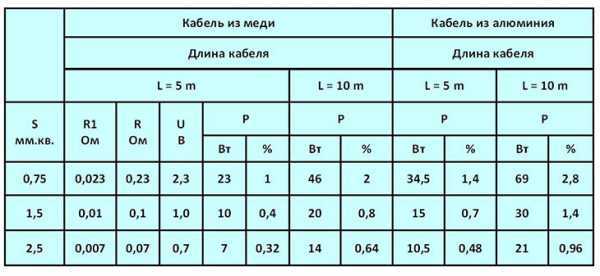
Если же нужно выполнить приближенный расчет, можно принять индуктивные сопротивления:

• для кабелей сечением 16 – 240 мм2 х = 0,06 Ом/км для напряжения до 1000 В;
• для кабелей сечением 16 – 240 мм2 х = 0,08 Ом/км для напряжения 6 – 10 кВ;
• для проводов проложенных на роликах х = 0,20 Ом/км;
• для проводов проложенных на изоляторах х = 0,25 Ом/км;

Литература:

1. Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г. 2. Справочная книга электрика. Григорьева В.И. 2004 г.

raschet.info