Емкостное сопротивление конденсатора: влияние на переменный и постоянный ток, формулы для расчета

§ 66. Цепь переменного тока, содержащая емкость

Если в цепь постоянного тока включить конденсатор (идеальный — без потерь), то в течение очень короткого времени после включения по цепи потечет зарядный ток. После того как конденсатор зарядится до напряжения, равного напряжению источника, кратковременный ток в цепи прекратится. Следовательно, для постоянного тока конденсатор представляет собой разрыв цепи, или, иными словами, бесконечно большое сопротивление.

Если же конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном, то в другом направлении.

При этом в цепи будет проходить переменный ток. Рассмотрим это явление подробнее.

В момент включения напряжение на конденсаторе равно нулю. В течение первой четверти периода, когда напряжение сети будет возрастать (рис. 143), конденсатор будет заряжаться.

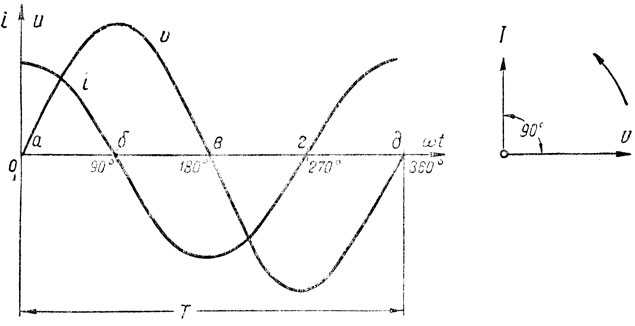Рис. 143. Графики и векторная диаграмма для цепи переменного тока, содержащей емкость

По мере накопления зарядов на обкладках конденсатора напряжение конденсатора увеличивается. Когда напряжение сети к концу первой четверти периода достигнет максимального значения U_m, напряжение конденсатора также станет равным U_m, заряд конденсатора прекращается и ток в цепи становится равным нулю.

Ток в цепи конденсатора можно определить по формуле

i = Δq/_Δt,

где Δq — количество электричества, протекающее по цепи за время Δt.

Из электростатики известно:

q = Cu_C = Cu,

где С — емкость конденсатора;

u — напряжение сети;

u_С — напряжение конденсатора.

Окончательно для тока имеем

i = C Δu_C/_Δt = C Δu/_Δt.

Из последнего выражения видно, что, когда Δu/_Δt максимально (положения а, в, д), i также максимально.

Когда Δu/_Δt = 0 (положения б, г на рис. 143), то i также равно нулю.

Во вторую четверть периода напряжение сети будет уменьшаться, и конденсатор начнет разряжаться. Ток в цепи меняет свое направление на обратное.

В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд.

Из рис. 143 видно, что ток I в цепи с емкостью в своих изменениях опережает по фазе напряжение конденсатора на 1/4 периода, или 90°.

Сравнивая векторные диаграммы цепей с индуктивностью и емкостью, мы видим, что индуктивность и емкость на фазу тока влияют прямо противоположно.

Пользуясь высшей математикой, можно доказать, что ток в цепи с емкостью пропорционален напряжению U_С, приложенному к конденсатору, угловой частоте со и величине емкости конденсатора С;

I = U_СωС = 2πfСU_С.

Обозначим

x_C = 1/_2πfC = 1/_ωC.

Величина x_С называется емкостным сопротивлением, или реактивным сопротивлением емкости, и измеряется в омах. Выражение закона Ома для цепи переменного тока, содержащей емкость, имеет вид

I = U/_{x_C}.

Та часть напряжения сети, которая приложена к конденсатору, называется емкостным падением напряжения (или реактивной слагающей напряжения) и обозначается U_C:

U_C = I ⋅ x_C.

Емкостное сопротивление х_С, так же как индуктивное сопротивление x_L, зависит от частоты переменного тока.

Но если с увеличением частоты индуктивное сопротивление увеличивается, то емкостное сопротивление, наоборот, будет уменьшаться.

Пример 6. Определить сопротивление конденсатора емкостью 5 мкф при частоте 50 гц:

x_С = 1/_2πfС = 1/_{2⋅3,14⋅50⋅5⋅10-6} = 636 ом,

при частоте 400 гц:

x_С = 1/_{2⋅3,14⋅400⋅5⋅10-6} = 79,5 ом.

На рис. 144 показана кривая мгновенной мощности в цепи с емкостью. Из чертежа видно, что в первую четверть периода цепь с емкостью забирает из сети энергию, которая запасается в электрическом поле конденсатора.

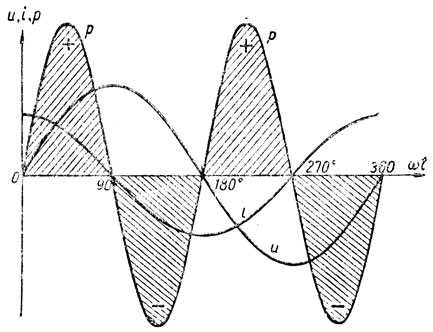Рис. 144. Кривая мгновенной мощности в цепи с емкостью

Энергию, запасаемую конденсатором к моменту, когда напряжение на нем равно максимальному значению, можно определить по известной формуле CU_м2/₂.

В следующую четверть периода конденсатор разряжается на сеть, отдавая ей ранее запасенную в нем энергию.

За вторую половину периода явление колебаний энергии повторяется. Таким образом, в цепи с емкостью происходит лишь обмен энергией между сетью и конденсатором без ее потерь.

Поэтому средняя за период мощность, или активная мощность, цепи с емкостью равна нулю, как и в цепи с индуктивностью.

Из графика, изображенного на рис. 144, видно, что мгновенная мощность в цепи с емкостью два раза в течение каждого периода (когда ωt = 45°, 135° и т. д.) достигает максимального значения, равного U_м/_√2 ⋅ I_м/_√2 = UI.

Этой величиной принято характеризовать количественно процесс обмена энергии между источником и электрическим полем конденсатора. Ее также называют реактивной мощностью и обозначают буквой Q.

Учитывая, что в рассматриваемой цепи U = Ix_C, получим следующее выражение для реактивной мощности:

Q = I2x_C.

Измерение и проверка

Измерить целостность конденсатора и его сопротивление можно при помощи мультиметра. Перед этим элемент обязательно необходимо отсоединить от цепи.

Проверка

Диагностика целостности конденсатора начинается с визуально осмотра его состояния. Любые трещины, вздутия или деформации корпуса можно считать неисправностью элемента. Если визуальный осмотр не дал никаких результатов, то элемент проверяется на пробой при помощи тестера.

Делается такая проверка следующим образом:

Элемент необходимо выпаять из схемы, а его контактные выводы замкнуть металлическим предметом для разрядки.
Мультиметр перемести в режим замера сопротивления.
Измерительные щупы соединить с контактами устройства.
Сопротивление исправного элемента будет измеряться бесконечным значением, которое будет превышать значение сопротивления утечки. Величина этой утечки при этом составляет 2 кОм.

Если показания меньше этого значения, значит элемент неисправен и пробит.

Замер

Замерить сопротивление можно так же с помощью мультиметра. Его надо будет перевести в режим измерения сопротивлений более 100 кОм. Далее необходимо соединить щупы прибора с контактами устройства. Некоторое время потребуется на полную зарядку элемента. После этого он покажет конечный результат, который не должен быть выше 100 кОм. Если этот порог преодолен, то можно сделать однозначный вывод о неисправности элемента.

Измерение емкости

Для замера емкости потребуется тестер с режимом СX. Если такого режима нет, проверить элемент будет невозможно. Далее требуется:

Полностью разрядить конденсатор.
На мультиметре выбирается режим СX.
Измерительные щупы соединить с контактными выводами устройства, строго соблюдая полярность.
Прибор должен показать величину больше 1, но при этом ее значение должно быть в пределах тех значений, которые указаны на корпусе детали. Если значение равняется 0 или находится за пределами указанных значений, то конденсатор можно признать неисправным.

Полученные мультиметром данные также можно считать ёмкостным значением, так как в момент проверки элемент проходит зарядку током.

Емкостным сопротивлением обладают все цепи, в которых задействованы конденсаторы. Зная, какой по параметрам элемент включен в данную цепь, можно легко рассчитать его емкостное влияние на цепь, используя представленные в статье формулы для расчётов.

Конденсатор емкостью C имеет в цепи постоянного тока бесконечно большое сопротивление. Если же приложить к конденсатору переменное напряжение, то он будет периодически перезаряжаться, и в цепи потечет ток. Напряжение на конденсаторе достигает максимального значения в те моменты, когда ток равен нулю.

Если R = 0, то напряжение на конденсаторе совпадает с приложенным напряжением и u = q/C. Мгновенное значение тока определяется выражением:

Между напряжением и током имеется разность фаз —π/2.

В чисто емкостной цепи переменного тока ток опережает напряжение на π/2 (или Т/4).

В соответствии с приведенным выше уравнением амплитуда тока I_m = ωCU_m. Сравнение с законом Ома U = RI показывает, что величина 1/ωС играет роль сопротивления.

Цепь переменного тока, содержащая емкость C, обладает сопротивлением переменному току; оно называется емкостным сопротивлением Х_C.

Единица СИ емкостного сопротивления: [X_C] = Ом.

Х_C	емкостное сопротивление цепи переменного тока,	Ом
ω = 2πf	круговая частота переменного тока,	радиан/Секунда
C	емкость,	Фарад

При увеличении частоты емкостное сопротивление уменьшается. Для постоянного тока (f = 0) оно бесконечно велико.

Ток в цепи, обладающей только емкостным сопротивлением, определяется выражением

Драйвер для светодиодов своими руками с питанием от 220 В: как сделать, схема простого самодельного стабилизатора напряжения для работы лед светильника от сети
Катушка индуктивности — что это такое? Магнитные поля. Электрическая индуктивность и ее применение.
Мигает светодиодный прожектор: во включенном состоянии и после выключения, не горит, причина, мерцает, стал тускло светить

Что надо знать про электрические процессы

Если говорить простым языком, то под сопротивлением принято понимать свойство среды, по которой протекает электрический ток, снижающее его величину.

Так работают провода и изоляторы высоковольтной линии электропередач, показанные на верхней картинке, да и любое вещество.

Изоляторы обладают очень высокими диэлектрическими свойствами, изолируют высоковольтное напряжение, присутствующее на токоведущих шинах от контура земли. Это их основное назначение.

Провода же должны максимально эффективно передавать транслируемые по ним мощности. Их создают так, чтобы они обладали минимальным электрическим сопротивлением, работали с наименьшими потерями энергии на нагрев.

В этом случае передача электричества от источника напряжения к потребителю на любое расстояние будет проходить эффективно.

Приведу для примера картинку из предыдущей моей статьи.

Ее, как и верхнюю, можно представить таким обобщенным видом.

На внешнем участке цепи токоведущие жилы отделены друг от друга воздушной средой и слоем изоляции с высокими диэлектрическими свойствами.

Хорошей проводимостью обладают токоведущие жилы. Подключенный к ним электрический прибор функционирует оптимально.

Как работает резистор

Ток в металлах проходит под действием приложенного напряжения за счет направленного движения электронов. При этом они соударяются, встречаются с положительно и отрицательно заряженными ионами.

Такие столкновения повышают температуру среды, уменьшают силу тока.

За направление электрического тока в электротехнике принято движение заряженных частиц от плюса к минусу. Электроны же движутся от катода к аноду.

Электрическое сопротивление металла зависит от его структуры и геометрических размеров.

Аналогичные процессы протекают в любой другой токопроводящей среде, включая газы или жидкости.

Какие существуют виды сопротивлений

В домашних электрических приборах используется большое разнообразие резисторов с постоянной или регулируемой величиной.

Они ограничивают величину тока всех бытовых устройств, а в наиболее сложных модулях их количество может достигать тысячи или более. Резисторы работают практически во всех схемах.

При использовании в цепях переменного тока они обладают активным сопротивлением, а конденсаторы и дроссели — реактивным.

Причем, на конденсаторах создается емкостное сопротивление, а у дросселей — индуктивное.

Реактивная составляющая на конденсаторах и дросселях сильно зависит от частоты электромагнитного колебания.

2 Шутки электриков о токах через конденсатор и дроссель

Их я привожу потому, что они позволяют запомнить характер прохождения тока через реактивные элементы.

Шутка №1 о емкости

В домашней сети и внутри многих приборов работают переменный и постоянный токи. Они по-разному ведут себя, если встречают на своем пути конденсатор.

Поскольку он состоит из двух токопроводящих пластин, разделенных слоем диэлектрика, то его обозначают на схемах двумя жирными черточками, расположенными параллельно. К их серединам подключены провода, нарисованные перпендикулярными линиями.

Переменный ток имеет форму гармоничной синусоиды, состоящей из двух симметричных половинок.

Такая гармоника движется от начала координат, встречает на своем пути обкладки, переваливается через них и, скатившись, начинает обгонять приложенное напряжение.

Постоянный ток таким свойством не обладает. Его тупой конец просто упирается в обкладку и останавливается. Пройти через конденсатор он не может. Это для него непреодолимое препятствие.

Шутка №2 о дросселе

Индуктивность выполнена витками изолированного провода. Любой ток проходит по нему. Но синусоида своими волнами путается в витках катушки, начинает отставать от напряжения.

Постоянка же спокойно перемещается внутри провода дросселя без ощущения какого-либо значительного противодействия. Поэтому постоянное напряжение может своим током спалить дроссель, созданный для работы на переменке.

Что же это за зверь: сверхпроводимость

Сто лет назад выявлена способность определенных металлов полностью терять свое сопротивление электрическому току при сверхнизких температурах. Выглядит этот процесс следующим образом.

Со сверхпроводниками домашний мастер не работает

Но на верхнюю часть приведенного графика рекомендую обратить внимание: нагрев металла повышает его электрическое сопротивление

При электротехнических расчетах, требующих получения точного результата, необходимо учитывать температурный коэффициент, взятый из справочников.

Принятые единицы измерения

При использовании закона Ома для практических расчетов все математические вычисления выполняются в установленных единицах измерений для всех 3-х величин:

Сила тока – в амперах (А).
Напряжение – в вольтах (В/V).
Сопротивление – в омах (Ом).

Исходные данные и другие параметры, представленные в единицах, должны переводиться в общепринятые значения.

Действие основных единиц и физическое соблюдение закона Ома невозможно в следующих ситуациях:

Наличие высоких частот, при которых электрическое поле изменяется с большой скоростью.
Низкотемпературный режим и сверхпроводимость.
Сильно разогретые спирали ламп накаливания, когда отсутствует линейность напряжения.
Пробой проводника или диэлектрика, вызванный высоким напряжением.
Электронные и вакуумные лампы, заполненные газами.
Полупроводники с р-п-переходами, в том числе, диоды и транзисторы.

Сила тока

Сила тока возникает при наличии частиц со свободными зарядами. Они перемещаются через поперечное сечение проводника из одной точки в другую. Источник питания создает электрическое поле, под действием которого электроны начинают двигаться упорядоченно.

Таким образом, сила тока является количеством электричества, проходящего через определенное сечение за единицу времени. Увеличить этот показатель можно путем увеличения мощности источника тока или изъятия из цепи резистивных элементов.

Международная единица СИ для тока – ампер. Это довольно большая величина, поскольку для человека смертельно опасными считаются всего 0,1 А. В электротехнике малые величины могут выражаться в микро- и миллиамперах.

Кроме того, сила тока может записываться с помощью основной формулы, когда известны значения напряжения и сопротивления. В числом виде она будет гласить следующее:

I = U/R

Сопротивление

Рассматривая закон ома для участка цепи, нельзя забывать о таком понятии, как сопротивление. Данная величина считается основной характеристикой проводника, поскольку именно сопротивление влияет на качество проводимости. Разные материалы проводят ток лучше или хуже. Это объясняется неоднородностью их структуры, различиями в кристаллических решетках. Поэтому в одних случаях электроны движутся с большей скоростью, а в других – с меньшей.

Собственным электрическим сопротивлением обладают все проводники, находящиеся в твердом, жидком, газообразном и плазменном состоянии. У каждого из них своя характеристика, называемая удельным сопротивлением. Данная величина отражает способность каждого материала к сопротивлению. За эталон принимается проводник длиной 1 м с поперечным сечением 1 м².

По закону Ома на участке цепи эта величина определяется: R = U/I.

Напряжение

Напряжение относится к важным характеристикам электрического тока, протекающего в проводнике. С физической точки зрения, это работа электрического поля, которое перемещает заряд на какое-то расстояние. В электротехнике напряжением считается разность потенциалов между двумя точками участка цепи. На практике эта величина служит для определения возможности подключения к сети потребителей электроэнергии, продолжительность их работы в этом состоянии.

В электрической цепи напряжение возникает следующим образом:

Вначале цепь подключается к источнику тока путем соединения с двумя полюсами. Это может быть генератор или батарея.
На одном полюсе или клемме – избыточное количество электроном, а на другом – их недостает. Первый условно считается положительным, второй – отрицательным.
Электрическое поле источника энергии воздействуют на электроны положительного полюса и самого проводника, заставляя их двигаться в сторону отрицательного полюса и притягиваться к нему. Такое притяжение происходит из-за положительного заряда на этом полюсе, поскольку электроны здесь отсутствуют.
Между обеими клеммами возникает разность потенциалов с определенным значением, что приводит к упорядоченному движению электронов в проводниках и подключенных нагрузках. Постепенно избыток электронов положительного полюса уменьшается, соответственно, снижается и потенциал. Характерным примером служит аккумуляторная батарея. При подключении нагрузки, ее потенциал будет падать, вплоть до полной разрядки. Для восстановления первоначальных свойств, потребуется подзарядка от постороннего источника тока.

При неизменной мощности источника энергии, значение напряжения может быть разным под действием следующих факторов:

Материал соединительных проводников. У каждого свой вольтамперный график.
Количество потребителей, подключенных к сети.
Температура окружающей среды.
Качество монтажа самой сети.

Осциллограмма силы тока на активном сопротивлении

В данном опыте нам не обязательно знать номинал силы тока в цепи. Мы будем просто смотреть, от чего зависит сила тока и изменяется ли вообще?

Поэтому, наша схема примет вот такой вид:

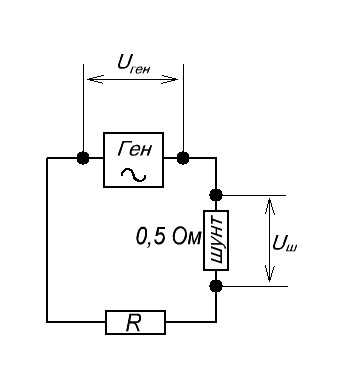
В этом случае шунтом будет являться резистор сопротивлением в 0,5 Ом. Почему именно 0,5 Ом? Да потому что он не будет сильно греться, так как обладает маленьким сопротивлением, а также его номинал вполне достаточен, чтобы снять с него напряжение.

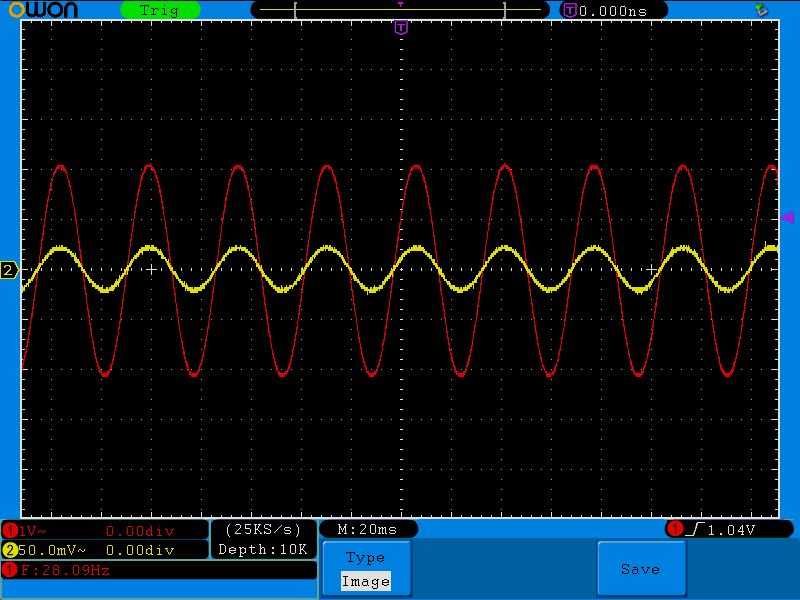
Осталось снять напряжение с генератора, а также со шунта с помощью осциллографа. Если вы не забыли, со шунта мы снимаем осциллограмму силы тока в цепи. Красная осциллограмма — это напряжение с генератора U_ген, а желтая осциллограмма — это напряжение с шунта U_ш , в нашем случае — сила тока. Смотрим, что у нас получилось:

Частота 28 Герц:

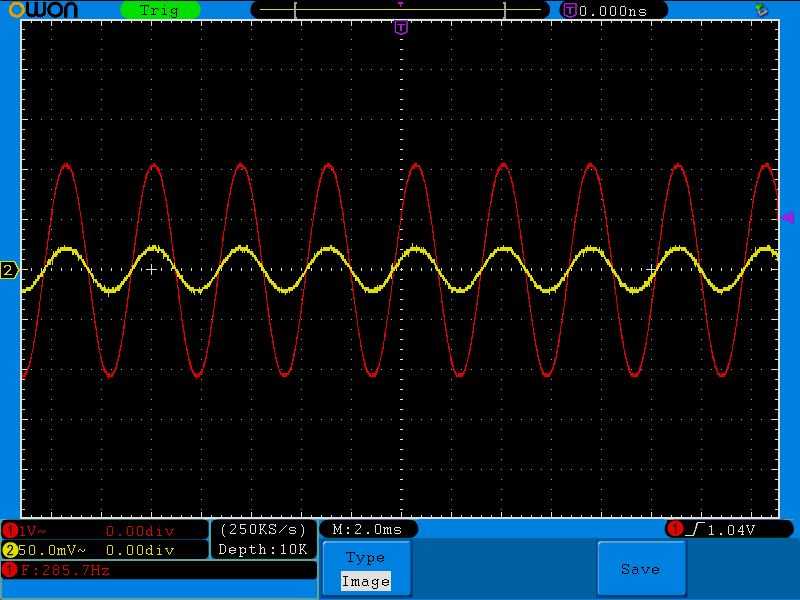
Частота 285 Герц:

Частота 30 Килогерц:

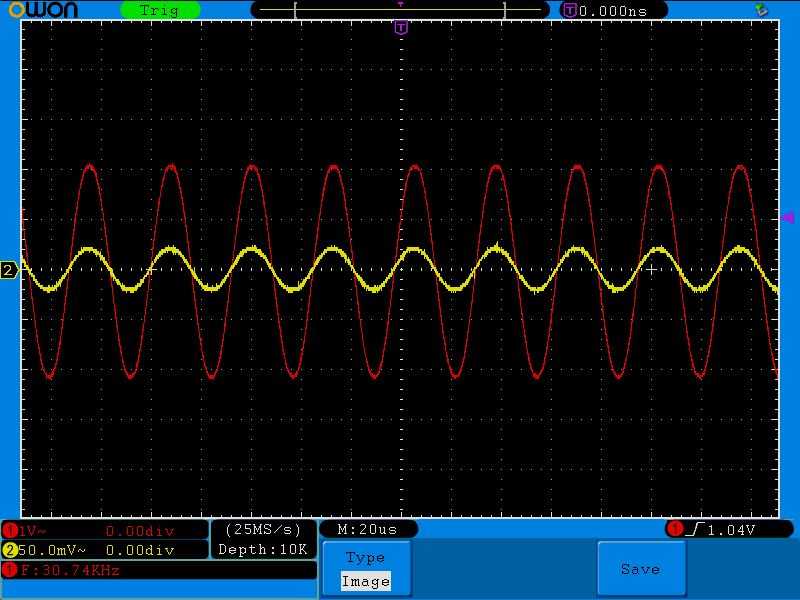
Как вы видите, с ростом частоты сила тока у нас осталась такой же.

Давайте побалуемся формой сигнала:

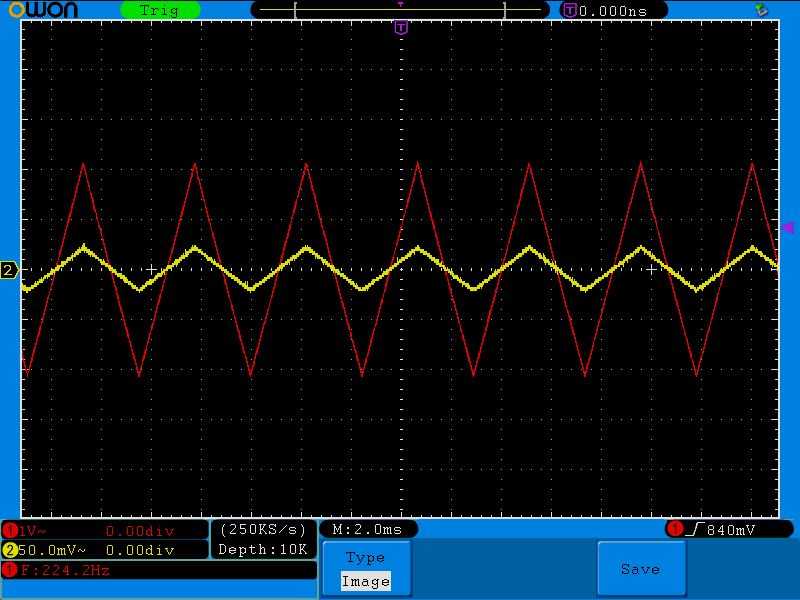
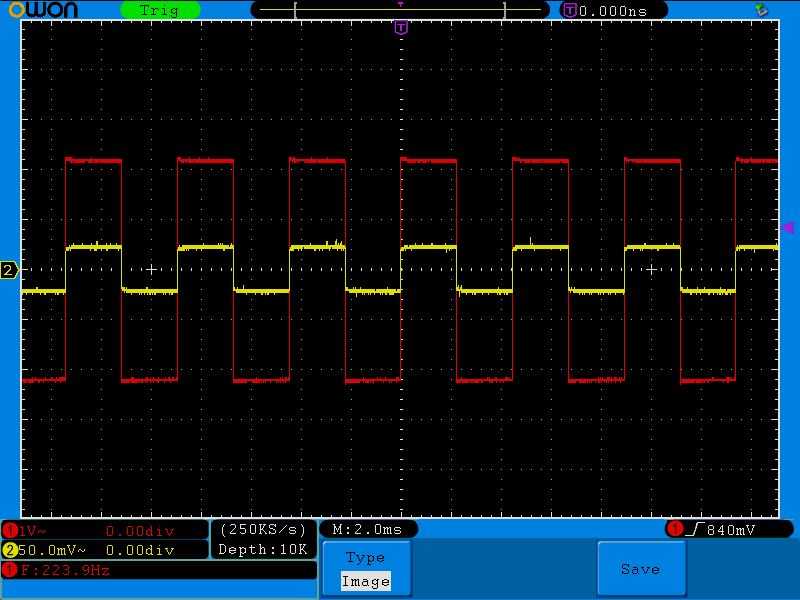
Как мы видим, сила тока полностью повторяет форму сигнала напряжения.

Итак, какие можно сделать выводы?

1) Сила тока через активное (омическое) сопротивление имеет такую же форму, как и форма напряжения.

2) Сила тока и напряжение на активном сопротивлении совпадают по фазе, то есть куда напряжение, туда и ток. Они двигаются синфазно, то есть одновременно.

3) С ростом частоты ничего не меняется (если только на очень высоких частотах).

Векторная диаграмма и полное сопротивление цели

Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:

u = u1R + uL + uC + u2R,

Имея в виду несовпадение по фазе активных и реактивных напряжений, общее напряжение получим векторным сложением:

U = U2R + UL + UC +U2R

Для построения векторной диаграммы находим:

U1R = IR1; U2R = IR2; UL = IXL; UC = IXC.

В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая:

1. ХL>ХC . Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U1 и U2 на этих элементах.

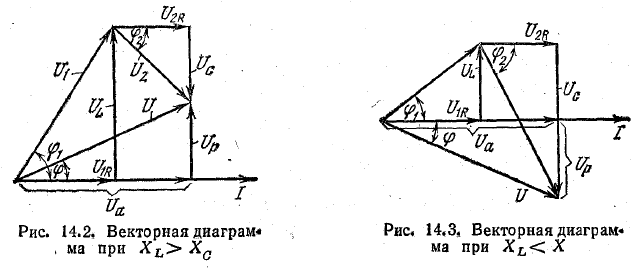
Векторная сумма напряжений U1 + U2 = U дает общее напряжение в цепи. Вместе с тем вектор U является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения цепи (Uа и Uр). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются: Ua = U1R + U2R.

Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: реактивное напряжение индуктивности считают положительным, а напряжение емкости — отрицательным: Uр = UL — UC .

При одинаковом токе во всех элементах цепи UL>UC . Ток отстает от общего напряжения по фазе на угол φ. Из треугольника напряжений следует

где R = R1 + R2 и X = XL — XC общее и активное и реактивное сопротивление цепи. Полное сопротивление цепи — Z.

Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.

Полное сопротивление цепи Z является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:

U = IZ; I = U/Z; Z = U/I.

Из треугольников напряжения и сопротивлений определяют следующие величины:

Угол сдвига по фазе между напряжением и током в цепи положительный (φ>0) (фазовые токи отсчитываются от вектора тока).

2. ХLCВекторная диаграмма изображена на рис. 14.3, где ULC , поэтому общее напряжение отстает от тока на угол φ

Реактивное сопротивление цепи носит емкостный характер.

Расчетные формулы для первого случая остаются без изменения и для второго случая.

3. XL = ХC . В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы: UL = UC (рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R.

Общее напряжение совпадает по фазе с током и равно по величине активной

составляющей напряжения.

Угол φ сдвига фаз между током и общим напряжением равен нулю.

Ток в цепи и общее напряжение связаны формулой

U = IR, или I = U/R.

В случае XL = ХC в цепи имеет место явление резонанса напряжений.

История накопителей заряда

Самое раннее письменное свидетельство получения зарядов с помощью трения принадлежит учёному Фалесу из Милета (635—543 гг. до н. э.), который описал трибоэлектрический эффект от взаимодействия янтаря и сухой шерсти. Для приблизительно 2300 последующих лет любое получение электричества заключалось в трении двух различных материалов друг о друга.

Качественный рывок в знаниях о зарядах произошёл в эпоху Просвещения — период революционного развития научной мысли в образованных кругах. В это время электричество становится популярной темой, а энтузиастами было произведено немало опытов и экспериментов с генераторами на основе трения.

Открытие явления произошло во время опытов у обоих экспериментаторов, но с той разницей, что Мюссенбрук, во-первых, сделал немало усовершенствований первоначально созданного оборудования, а во-вторых, письменно сообщил коллегам о своих достижениях. Прошло совсем немного времени и учёные мира стали создавать накопители зарядов собственных конструкций. Это были первые шаги в эволюции конденсаторов, продолжающейся и в наши дни. Основные даты хронологии появления устройств для хранения зарядов:

Что такое

Цепь, по которой протекает непостоянный ток, обладает полным сопротивлением. Вычисляется оно по сумме активного и реактивного сопротивлений, возведенных в квадрат.

Формула вычисления

Графическое изображение этой формулы представляет собой треугольник. Его катеты представлены активным и реактивным сопротивлениями, а гипотенуза полным электросопротивлением.

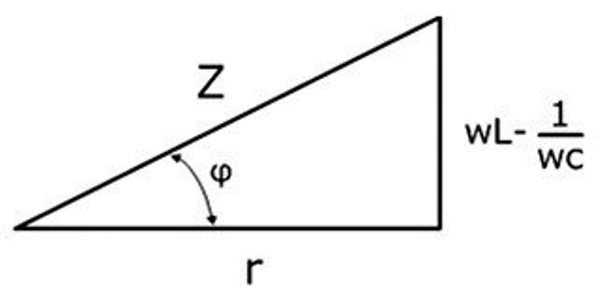
Графическое отображение формулы

Емкостное электросопротивление (Xc) является одним из видов реактивного сопротивления. Этот показатель характеризует противодействие электроемкости в цепи электротоку с переменными параметрами. Преобразование электроэнергии в тепловую в момент протекания электричества сквозь емкость не возникает (свойство реактивного сопротивления). Вместо этого осуществляется передача энергии электрического тока электрическому полю и обратно. Потерь энергии при таком обмене не происходит.

Емкостное сопротивление конденсатора можно сравнить с кастрюлей, наполняемой жидкостью, при полном заполнении ее объема она переворачивается, выливая содержимое, а затем наполняется заново. После достижения максимального заряда конденсатора происходит разрядка, затем он заряжается вновь.

Дополнительная информация: Конденсатор цепи способен накопить лишь ограниченную величину заряда до перемены полярности напряжения

По данной причине непостоянный ток не падает до нуля, важное отличие от постоянного электричества. Низкие значения частоты тока соответствуют низким показателям заряда, накопленного конденсатором, низким значениям противодействия электричеству, что придает реактивные свойства. По сути, Xc — это противостояние электродвижущей силы конденсатора, уровню его заряда

По сути, Xc — это противостояние электродвижущей силы конденсатора, уровню его заряда.

Сопротивление конденсатора.

Замкнем цепь. Конденсатор начал заряжаться и сразу стал источником тока, напряжения, Э. Д. С.. На рисунке видно что Э. Д. С. конденсатора направлена против заряжающего его источника тока.

Противодействие электродвижущей силы заряжаемого конденсатора заряду этого конденсатора называется емкостным сопротивлением.

Вся энергия затрачиваемая источником тока на преодоление емкостного
сопротивления превращается в энергию электрического поля конденсатора.
Когда конденсатор будет разряжаться вся энергия электрического поля
вернется обратно в цепь в виде энергии электрического тока. Таким
образом емкостное сопротивление является реактивным, т.е. не вызывающим безвозвратных потерь энергии.

Почему постоянный ток не проходит через конденсатор, а переменный ток проходит?

Включим цепь постоянного тока. Лампа вспыхнет и погаснет, почему? Потому что в цепи прошел ток заряда конденсатора. Как только конденсатор зарядится до напряжения батареи ток в цепи прекратится.

А теперь замкнем цепь переменного тока. В I четверти периода напряжение на генераторе возрастает от 0 до максимума. В цепи идет ток заряда конденсатора. Во II четверти периода напряжение на генераторе убывает до нуля. Конденсатор разряжается через генератор. После этого конденсатор вновь заряжается и разряжается. Таким образом в цепи идут токи заряда и разряда конденсатора. Лампочка будет гореть постоянно.

В цепи с конденсатором ток проходит во всей замкнутой цепи, в том числе и в диэлектрике конденсатора. В заряжающемся конденсаторе образуется электрическое поле которое поляризует диэлектрик. Поляризация это вращение электронов в атомах на вытянутых орбитах.

Одновременная поляризация огромного количества атомов образует ток, называемый током смещения.

Таким образом в проводах идет ток и в диэлектрике причем одинаковой величины.

конденсатора определяется по формуле

На активном сопротивлении напряжение U акт и ток I совпадают по фазе. На емкостном сопротивлении напряжение U c отстает от тока I на 90 0 . Результирующее напряжение приложенное генератором к конденсатору определяется по правилу параллелограмма. Это результирующее напряжение отстает от тока I на какой то угол φ всегда меньший 90 0 .

Импеданс элемента

Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе. Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние.

Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.

Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где

Xl — индуктивность;
Xс — ёмкость;
R — активная составляющая.

Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.

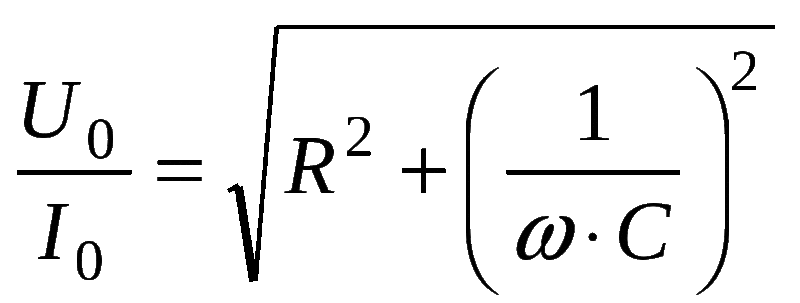
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:

X > 0, в элементе проявляются индуктивные свойства;
X = 0, в ёмкости присутствует только активная величина;
X < 0, в элементе проявляется ёмкостное сопротивление.

Ёмкостное сопротивление

Для понимания процесса следует представить конденсатор в электрической цепи, по которой течёт переменный ток. Причём в этой цепи нет других элементов. Значение тока, проходящего через конденсатор, и напряжения, приложенного к его обкладкам, изменяется по времени. Зная любое из этих значений, можно найти другое.

Пускай ток изменяется по синусоидальной зависимости I (t) = Im * sin (w*t+ f 0). Тогда напряжение можно описать как U (t) = (Im/C*w) *sin (w*t+ f 0 -p/2). При учёте в формуле сдвига фаз на 90 градусов, возникающего между сигналами, вводится комплексная величина j, называемая мнимой единицей. Поэтому формула для нахождения тока будет выглядеть как I = U /(1/j*w*C). Но учитывая, что комплексное число только обозначает смещение напряжения относительно тока, а на их амплитудные значения не влияет, его можно убрать из формулы, тем самым значительно её упростив.

Так как по закону Ома сопротивление прямо пропорционально напряжению на участке цепи и обратно пропорционально току, то преобразуя формулы, можно будет получить следующее выражение:

Xc = 1/w*C = ½*p*f*C. Единица измерения — ом.

Становится понятно, что ёмкостное сопротивление зависит не только от ёмкости, но и от частоты. При этом чем больше эта частота, тем меньшее сопротивление конденсатор будет оказывать проходимому через него току. По отношению к ёмкости это утверждение будет обратным. Вот поэтому для постоянного тока, частота которого равна нулю, сопротивление накопителя будет бесконечно большим.

На практике всё немного по-другому. Чем ближе частота сигнала приближается к нулевому значению, тем больше становится сопротивление конденсатора, но при этом разрыв цепи наступить всё равно не может. Связанно это с током утечки. В случае когда частота стремится к бесконечности, сопротивление конденсатора должно становиться нулевым, но этого тоже не происходит — из-за присутствия паразитной индуктивности и всё того же тока утечки.

Индуктивная составляющая

При прохождении переменного сигнала через накопитель, его можно представить в виде последовательно включённой с источником питания катушки индуктивности. Эта катушка характеризуется большим сопротивлением в цепи переменного сигнала, чем постоянного. Значение силы тока в определённой точке времени находится как I = I 0 * sinw .

Приняв во внимание, что мгновенная величина напряжения U 0 обратна по знаку мгновенному значению ЭДС самоиндукции E 0, а также используя правило Ленца, можно получить выражение E = L * I, где L — индуктивность

Следовательно: U = L*w * I 0 *cosw*t = U 0 *sin (wt + p /2) , причём ток отстаёт от напряжения на p /2. Используя закон Ома и приняв, что сопротивление катушки равно w * L, получится формула для участка электрической цепи, имеющая только индуктивную составляющую: U 0 = I 0 / w * L.