Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях — Help for engineer
Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях
Делитель напряжения используется в электрических цепях, если необходимо понизить напряжение и получить несколько его фиксированных значений. Состоит он из двух и более элементов (резисторов, реактивных сопротивлений). Элементарный делитель можно представить как два участка цепи, называемые плечами. Участок между положительным напряжением и нулевой точкой – верхнее плечо, между нулевой и минусом – нижнее плечо.
Делитель напряжения на резисторах может применятmся как для постоянного, так и для переменного напряжений. Применяется для низкого напряжения и не предназначен для питания мощных машин. Простейший делитель состоит из двух последовательно соединенных резисторов:
На резистивный делитель напряжения подается напряжение питающей сети U, на каждом из сопротивлений R1 и R2 происходит падение напряжения. Сумма U1 и U2 и будет равна значению U.
В соответствии с законом Ома (1):
Падение напряжения будет прямо пропорционально значению сопротивления и величине тока. Согласно первому закону Кирхгофа, величина тока, протекающего через сопротивления одинакова. С чего следует, что падение напряжения на каждом резисторе (2,3):
Тогда напряжение на всем участке цепи (4):
Отсюда определим, чему равно значение тока без включения нагрузки (5):
Если подставить данное выражение в (2 и 3), то получим формулы расчета падения напряжения для делителя напряжения на резисторах (6, 7):
Необходимо упомянуть, что значения сопротивлений делителя должны быть на порядок или два (все зависит от требуемой точности питания) меньше, чем сопротивление нагрузки. Если же это условие не выполняется, то при приведенном расчете подаваемое напряжение будет посчитано очень грубо.
Для повышения точности необходимо сопротивление нагрузки принять как параллельно подсоединенный резистор к делителю. А также использовать прецизионные (высокоточные) сопротивления.
Онлайн подбор сопротивлений для делителя
Пусть источник питания выдает 24 В постоянного напряжения, примем, что величина сопротивления нагрузки переменная, но минимальное значение равно 15 кОм. Необходимо рассчитать параметры резисторов для делителя, выходное напряжение которого равно 6 В.
Таким образом, напряжения: U=24 B, U2=6 В; сопротивление резисторов не должно превышать 1,5 кОм (в десять раз меньше значения нагрузки). Принимаем R1=1000 Ом, тогда используя формулу (7) получим:
выразим отсюда R2:
Зная величины сопротивления обоих резисторов, найдем падение напряжения на первом плече (6):
Ток, который протекает через делитель, находится по формуле (5):
Схема делителя напряжения на резисторах рассчитана выше и промоделирована:
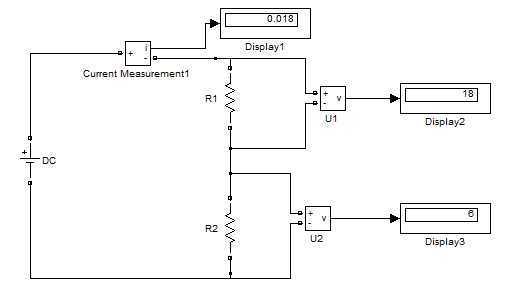
Использование делителя напряжения очень неэкономичный, затратный способ понижения величины напряжения, так как неиспользуемая энергия рассеивается на сопротивлении (превращается в тепловую энергию). КПД очень низкий, а потери мощности на резисторах вычисляются формулами (8,9):
По заданным условиям, для реализации схемы делителя напряжения необходимы два резистора:
| 1. R1=1 кОм, P1=0,324 Вт. | ||
| 2. R2=333,3 Ом, P2=0,108 Вт. |
Полная мощность, которая потеряется:
Делитель напряжения на конденсаторах применяется в схемах высокого переменного напряжения, в данном случае имеет место реактивное сопротивление.
Сопротивление конденсатора рассчитывается по формуле (10):
| где С – ёмкость конденсатора, Ф; | ||
| f – частота сети, Гц. |
Исходя из формулы (10), видно, что сопротивление конденсатора зависит от двух параметров: С и f. Чем больше ёмкость конденсатора, тем сопротивление его ниже (обратная пропорциональность). Для ёмкостного делителя расчет имеет такой вид (11, 12):
Еще один делитель напряжения на реактивных элементах – индуктивный, который нашел применение в измерительной технике. Сопротивление индуктивного элемента при переменном напряжении прямо пропорционально величине индуктивности (13):
| где L – индуктивность, Гн. |
Падение напряжения на индуктивностях (14,15):
Как рассчитать максимальную силу переменного тока на входе
УП-21
Знать максимальный входной ток источника питания полезно при выборе требований к электросети, аварийного выключателя, кабеля питания переменного тока, разъемов и даже изолирующего трансформатора в плавучих блоках. Рассчитать максимальную силу входного тока довольно просто, зная несколько основных параметров и простых математических действий.
Номинальная мощность источника питания высокого напряженияДля всех источников питания компании Spellman указана номинальная максимальная мощность в ваттах. Это первый нужный нам параметр; получить его можно из техпаспорта изделия. У большей части источников питания компании Spellman максимальная номинальная мощность указана в номере модели. Например, SL30P300/115 — источник питания напряжением 30 кВ с положительной полярностью и максимальной мощностью 300 Вт, работающий от входного напряжения переменного тока 115 В.
КПД источника питания КПД источника питания — отношение мощности на входе к мощности на выходе. КПД обычно указывается в процентном виде или в виде десятичной дроби меньше 1, например, 80 % или 0,8. Чтобы узнать входную мощность, поделим максимальную выходную мощность на КПД:
300 Вт / 0,8 = 375 Вт
Коэффициент мощностиКоэффициент мощности — отношение реальной мощности к фиксируемой. Обычно он выражается в виде десятичной дроби меньше 1. Реальная мощность указывается в ваттах, а фиксируемая — в вольт-амперах (ВА). У однофазных импульсных источников питания без коррекции коэффициент мощности обычно довольно низок, например, 0,65. Импульсные источники питания без коррекции обладают более высоким коэффициентом мощности, например, 0,85. Блоки питания с активной коррекцией коэффициента мощности могут обладать очень высоким коэффициентом мощности, к примеру, 0,98. В приведенном выше примере используется источник питания без коррекции с питанием от однофазной линии, таким образом:
375 Вт / 0,65 = 577 ВА
Напряжение на входеНам необходимо знать входное напряжение переменного тока, для которого предназначен источник питания. В приведенном выше примере оно составляет 115 В. Это номинальное напряжение, в реальности оно указывается с допуском ±10 %. Чтобы предусмотреть наихудший случай с низким напряжением в сети, отнимем 10 %:
В приведенном выше примере оно составляет 115 В. Это номинальное напряжение, в реальности оно указывается с допуском ±10 %. Чтобы предусмотреть наихудший случай с низким напряжением в сети, отнимем 10 %:
115 В – 10 % = 103,5 В
Максимальная сила переменного тока на входеВзяв 577 ВА и разделив ее на 103,5 В, получаем:
577 ВА / 103,5 В = 5,57 А
Если напряжение на входе однофазное, наш ответ — 5,57 А.
Трехфазное входное напряжениеИсточники питания с трехфазным напряжением на входе обладают более высоким коэффициент мощности, чем однофазные. Кроме того, по причине наличия трех фаз, питающих источник, фазовая сила тока будет меньшей. Чтобы узнать силу тока одной фазы, поделим рассчитанную нами силу тока на входе на √3 (1,73).
Рассчитаем данные для следующего примера: STR10N6/208. Из технического паспорта STR узнаем, что максимальная мощность — 6000 Вт, КПД 90 %, а коэффициент мощности 0,85. И хотя STR в силу своей конструкции будет работать с напряжением до 180 В переменного тока, в данном примере его питание будет поступать от трехфазной сети 208 В. Максимальную силу входного тока на одну фазу получаем следующим образом:
Максимальную силу входного тока на одну фазу получаем следующим образом:
КПД источника питания: 6000 Вт / 0,9 = 6666 Вт
Коэффициент мощности:6666 Вт / 0,85 = 7843 ВА
Напряжение на входе:208 В – 10 % = 187 В
Максимальная сила переменного тока на входе:7843 ВА / 187 В = 41,94 А (если бы сеть была однофазной)
Пересчет для трех фаз на входе:41,94 А / √3 (1,73) = 24,21 А на фазу
Таким образом, у нас есть два уравнения, одно для однофазного и одно для трехфазного напряжения на входе:
Уравнение для максимальной силы однофазного входного токаВходной ток = максимальная мощность/(КПД)(коэффициент мощности)(максимальное входное напряжение)
Уравнение для максимальной силы трехфазного входного токаВходной ток = максимальная мощность/(КПД)(коэффициент мощности)(максимальное входное напряжение)(√3)
Данные расчеты входного тока предусматривают наихудший случай, исходя из того, что источник питания работает на максимальной мощности с низким напряжением в линии, а также с учетом КПД и коэффициента мощности.
Делитель с Ардуино

Конечно ты мог установите делитель напряжения на макетную плату и интегрируйте его в свои проекты Arduino без труда. И он не только служит для разделения напряжений, как мы видели, вы можете разделить эти делители, вставив другие элементы, такие как кнопки или переключатели, чтобы с помощью одного и того же источника питания вы могли управлять несколькими устройствами на выходе. Например, простой делитель, подключенный к плате Arduino UNO Чтобы прочитать значения из серии
El код для Arduino IDE Это было бы примерно так:
void setup() {
Serial.begin(9600);
}
</span>void loop() {
int sensorValue = analogRead(A0);
Serial.println(sensorValue);
}
Больше информации — Наш курс Arduino в PDF
Параллельное и последовательное соединение резисторов, решение задач
Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно. Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. На схеме присутствует параллельная и последовательная часть соединения элементов
Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1). Как же правильно определить параллельное и последовательное соединение резисторов?
Будет интересно Как прочитать обозначение (маркировку) резисторов
Будет интересно Как прочитать обозначение (маркировку) резисторов
Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.
Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом.
Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше. Теперь образовалась ситуация — включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом
Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех. Заменяем эти сопротивление одним эквивалентным R23465
В конечном итоге все выглядит уже намного проще
Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом
В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом.
Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.
Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно. На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.
Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
- Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
- Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.
Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Типы подключений.
Есть ли умножители напряжения?

Да, есть умножители напряжения. В этом случае это также простая схема, включающая параллельно диоды. Это дает обратный эффект, умножая входное напряжение на различные коэффициенты, чтобы получить более высокие напряжения. Фактически, это принцип, используемый в известных инверторах ноутбуков, которые сильно нагреваются, оставляя более горячую область за экраном …
те инверторы — это не что иное, как схема с включенными параллельно диодами для увеличения мощности, обеспечиваемой аккумулятором портативного компьютера, для питания некоторых типов панелей дисплея. На каждом этапе он набирает напряжение, пока не достигнет искомого высокого напряжения, вы даже можете заставить батарею в несколько вольт получить сотни или тысячи вольт.
Другие делители / множители
Очевидно электроника сильно продвинулась и это позволяет интегрировать схемы этого типа в единую микросхему. Кроме того, на рынке есть много производителей, которые реализуют другие типы делителей и умножителей в той же схеме. Те делители и умножители, о которых я говорю, являются тактовыми частотами. Но вы должны знать, что есть еще множители и делители интенсивности и т. Д.
Что такое внутреннее сопротивление?
Внутреннее сопротивление — это параметр, который является общим для каждого источника питания, но о нем часто забывают. Любой реальный источник напряжения можно в простейшем случае смоделировать, как последовательную комбинацию идеального источника и определенного сопротивления.
| Проще всего представить, батарейку или аккумулятор, внутри которого, есть резистор. |
Такое сопротивление никому не нужно, но с этим ничего не поделать; производители могут только стараться поддерживать это сопротивление на минимально возможном уровне. Это связано с составом контактных сопротивлений, крышек батарей, выводов и т.д. Кроме того, сопротивление может зависеть от температуры, сроков эксплуатации элементов и других факторов.
Это сопротивление нельзя точно самим рассчитать и не пытайтесь измерить его мультиметром! Такую информацию может предоставить только производитель батареи
К счастью, это для нас сейчас не важно, самое главное — просто знать о существовании внутреннего сопротивления
Наличие внутреннего сопротивления иллюстрирует очень простой опыт. Давайте измерим напряжение в цепи, при течении тока через резисторы 1 кОм и 10 кОм и без них. Вот очень простая схема измерения:
Примеры измерений:
| Резистор 1k подключен | Резистор 10 кОм подключен | Без резистора |
Как вы можете видеть в приведенном выше примере, увеличивая ток от батареи, мы получаем более низкое напряжение. Это можно прекрасно объяснить так: чем меньше R1 (который представляет собой нагрузку) по сравнению с R2 (которое представляет собой внутреннее сопротивление), тем большее напряжение подается на R2. Для многих измерение без резистора может вызывать недоумение, потому что они думают, что это означает отсутствие сопротивления — это неправильное мышление.
| Отсутствие резистора следует понимать как бесконечно большое сопротивление. Так как, в цепи не протекает ток и батарея никак не нагружается, поэтому измеренное напряжение является самым высоким. |
Помните, что при зарядке аккумулятора слишком большим током (через резистор с низким сопротивлением), аккумулятор может нагреться и выйти из строя (может произойти утечка электролита)! При потреблении большого тока, используйте источник с достаточно низким внутренним сопротивлением и достаточно большой мощностью.
| Вышеупомянутый феномен беспокоит многих новичков, пытающихся запитать свои проекты небольшими батареями (например, 9 В). Они забывают, что высокое потребление тока (например, моторами) вызывает падение напряжения на батарее. Это может помешать работе всей системы. |
Алгебраическая сумма разностей потенциалов
Закон напряжения по Густаву Кирхгофу – второй закон этого автора, используемый для анализа электрической цепи. Второй закон Кирхгофа гласит, что для последовательной замкнутой цепи алгебраическая сумма всех напряжений в круге любой замкнутой цепи равна нулю. Претензия связана с тем, что петля петли представляет собой замкнутый токопроводящий путь, где потери энергии исключены. Другими словами, алгебраическая сумма разностей потенциалов замкнутого контура теоретически равна нулю:
V = 0
Примечание. Термин «алгебраическая сумма» означает учет полярностей и знаков источников ЭДС, а также падения напряжения в цепи. Эта концепция закона Кирхгофа, известного как «сохранение энергии», как движение по контуру или замкнутому контуру, подтверждает логику возврата к началу цепи и к исходному потенциалу без потери напряжения во всей цепи.
Итак, вывод следует: при применении второго закона Кирхгофа к определенному элементу электрической цепи важно обращать особое внимание на алгебраические признаки падений напряжения на элементах (источниках ЭДС), иначе расчеты обернутся ошибкой
Одиночный контурный элемент — резистор
В качестве простого примера с резистором предположим, что ток течет в том же направлении, что и поток положительного заряда. В этом случае ток протекает через резистор от точки A к точке B. Действительно, от положительной клеммы к отрицательной. Следовательно, поскольку движение положительного заряда отмечается в направлении, аналогичном направлению протекания тока, на резистивном элементе будет зафиксировано падение потенциала, что приведет к падению отрицательного потенциала на резисторе (- I * R).
Если ток, протекающий из точки B в точку A, течет в направлении, противоположном потоку положительного заряда, вы заметите увеличение потенциала через резистивный элемент, поскольку происходит переход от отрицательного потенциала к положительному потенциалу, что дает падение напряжения. (+ I * R). Следовательно, чтобы правильно применить закон Кирхгофа к электрической цепи, необходимо точно определить направление полярности. Очевидно, знак падения напряжения на резисторе зависит от направления тока, протекающего через резистор.
Направление протекания тока в замкнутом контуре можно определять по или против часовой стрелки, и любой вариант допустим на выбор. Если выбранное направление отличается от фактического направления тока, соблюдение закона Кирхгофа будет правильным и действительным, но приведет к результату, когда алгебраический расчет имеет знак минус. Чтобы лучше понять эту концепцию, логично рассмотреть еще один пример с петлевой петлей на соответствие второму закону Кирхгофа.
Одиночный контур электрической цепи
Второй закон Кирхгофа гласит, что алгебраическая сумма разностей потенциалов каждого замкнутого контура равна нулю. Демонстрационная схема действия Второго закона Кирхгофа для замкнутой цепи с двумя резисторами и источником ЭДС. Если принять условие, что два резистора R1 и R2 соединены последовательно, оба элемента являются частью одной цепи. В результате через каждый из резисторов протекает одинаковый ток.
Таким образом, падение напряжения на резисторе R1 = I * R1 и падение напряжения на резисторе R2 = I * R2 дают напряжение согласно второму закону Кирхгофа:
V = I * Rs
где: Rs = R1 + R2.
Очевидно, что применение второго закона Кирхгофа к одиночному замкнутому контуру дает формулу для эквивалента или импеданса для последовательной цепи. Допускается расширить эту формулу для нахождения значений капель потенциала по контурной окружности:
I = V / Rs
Vr1 = V * (R1 / R1 + R2)
Vr2 = V * (R2 / R1 + R2)
Есть три резистора с номинальным сопротивлением 10, 20, 30 Ом соответственно. Все три резистивных элемента соединены последовательно с батареей на 12 вольт.
Необходимо рассчитать:
- полное сопротивление,
- ток цепи,
- ток через каждый резистор,
- падение напряжения на каждом резисторе.
Рассчитываем полное сопротивление:
Ro = R1 + R2 + R3 = 10 Ом + 20 Ом + 30 Ом = 60 Ом
Ток цепи:
I = V / Ro = 12/60 = 0,2 А (200 мА)
Ток через каждый резистор:
I * R1 = I * R2 = I * R3 = 0,2 А (200 мА)
Потенциальное падение на каждом из резисторов:
VR1 = I * R1 = 0,2 * 10 = 2 В
VR2 = I * R2 = 0,2 * 20 = 4 В
VR3 = I * R3 = 0,2 * 30 = 6 В
Таким образом, действует Второй закон Кирхгофа, поскольку отдельные падения напряжения, обнаруживаемые по окружности замкнутого контура, в конечном итоге являются суммой напряжений.
Последовательное соединение проводников
Параллельное и последовательное соединение резисторов, решение задач
Емкостной делитель напряжения
Простейший емкостной делитель напряжения состоит из двух последовательно соединенных конденсаторов и используется для снижения величины U на отдельных элементах электрической цепи.
Делитель постоянного напряжения на конденсаторах чаще всего применяют многоуровневых инверторов напряжения, широко используемых как на электроподвижном составе, так и в других направлениях силовой электроники.
Главная сложность практического применения такой схемы (и всех подобных схем) заключается в невозможности обеспечения равномерного разряда конденсаторов, вследствие чего напряжения на них будет распределяться не поровну. Чем сильнее разряжен один конденсатор по сравнению с другим (иди с другими), тем большая разница в U будет на них, что наглядно отображает формула:
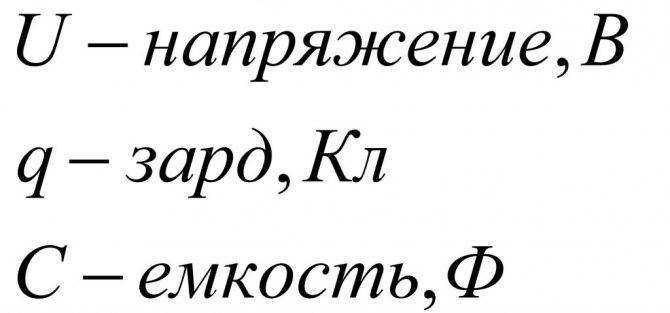
По этой причине подобные схемы крайне нестабильно работают и обязательно предусматривают узлов подзарядки конденсаторов с целью выравнивания напряжения на последних.
Емкостной делитель напряжения в цепи переменного тока
В радиоэлектронике в большей степени находят применение емкостные делители переменного напряжения.
Конденсатор, как и катушка индуктивности, относится к реактивному элементу, то есть потребляет реактивную мощность от источника переменного тока, в отличие от резистора, который является активным элементов и потребляет исключительно активную мощность.
Реактивный элемент
Здесь следует кратко пояснить разницу между активной и реактивной мощностями. Активная мощность выполняет полезную работу и реализуется только в том случае, когда ток и напряжение направлены в одном направлении и не отстают друг от друга, то есть находятся в одной фазе, что имеет место только на резисторе. На конденсаторе ток отстает от напряжения на угол φ = 90°. В результате чего ток напряжение находятся в противофазе, поэтому когда ток имеет максимальное значение напряжение равно нулю, а произведение этих двух величин дают мощность, которая в таком случае равна нулю, так как один из множителей равен нулю. Следовательно, мощность не потребляется.
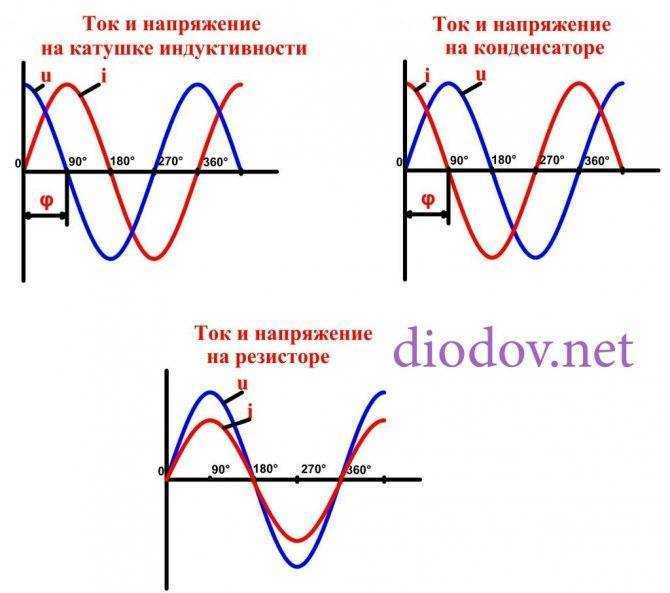
Аналогичные процессы протекают и в цепи с катушкой индуктивности. Разница лишь в том, что на индуктивности i отстает от u на угол φ = 90°.
Реактивная мощность проявляется только в цепях переменного тока. Она составляет часть полной мощности и определяется по формуле:

Реактивная мощность в отличие от активной, не потребляется нагрузкой, а циркулирует между источником питания и нагрузкой. Поэтому конденсатора и катушка индуктивности являются реактивными элементами, не потребляющими активную мощность и по этой причине они практически не нагреваются.
Расчет сопротивления делителя напряжения на конденсаторах заключается в определении необходимых значений сопротивлений.
Сопротивление конденсатора XC является величиной не постоянной и зависит от частоты переменного тока f и емкости C:
Как видно из формулы, сопротивление снижается с увеличением частоты и емкости. Для постоянного тока, частота которого равна нулю, сопротивление стремится к бесконечности, поэтому, рассматриваемая далее схема емкостного делителя напряжения не применяется постоянном токе.
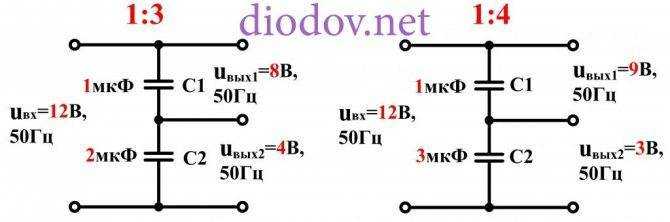
Для снижения величины uвых, например в два раза, емкости C1 и C2 должны быть равны. Универсальные формулами для определения выходных uвых1 и uвых2 в зависимости от входного и емкостей C1 и C2 имеют вид, аналогичный для резисторных делителей:
Поскольку частота переменного тока для всех конденсаторов одинакова, то формулу можно упростить:
Индуктивный делитель напряжения
В качестве делителей переменного напряжения также, но гораздо реже, применяют катушки индуктивности, которые относятся к реактивным элементам. Однако, в отличие от конденсаторов, которые являются накопителями электрического поля, катушки индуктивности накапливают магнитное поле.
Индуктивное сопротивление зависит от индуктивности L и частоты переменного тока f. С ростом этих параметров сопротивление катушки переменному току возрастает.
XL = 2πfL.
Упрощенный вариант формулы:
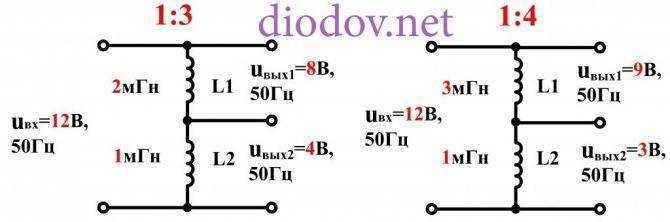
Как вы наверняка уже заметили, чтобы рассчитать емкостной делитель напряжения достаточно знать емкости конденсаторов, а индуктивный делитель – индуктивности.
- Делитель напряжения на резисторах
- Инвертор напряжения
- Умножитель напряжения
- Замена электролитического конденсатора
Маркировка переменных резисторов
Российская маркировка переменных сопротивлений до 1980 года – например, СП4-18:
- Тип изделия обозначается СП.
- Первая цифра – разновидность материала и технология изготовления – 4.
- Вторая – регистрационный номер типа резистора –18.
Маркировка группы по технологии изготовления и материалу:
- 1 – непроволочные тонкослойные углеродистые и бороуглеродистые;
- 2 – непроволочные тонкослойные металлопленочные и металлооксидные;
- 3 – непроволочные композиционные пленочные;
- 4 – непроволочные композиционные объемные;
- 5 – проволочные;
- 6 – непроволочные тонкослойные металлизированные.
Сейчас действует новая система маркировки переменных и подстроечных резисторов – например, РП1-46:
- Тип изделия обозначается РП.
- Первая цифра определяет группу по материалу резистивного элемента (1 – непроволочные, 2 – проволочные и металлофольговые).
- Вторая цифра – регистрационный номер разработки конкретного типа сопротивления.
Таблица номиналов
| 1 Ом | 10 Ом | 100 Ом | 1 кОм | 10 кОм | 100 кОм | 1 МОм | 10 МОм |
| 1.5 Ом | 15 Ом | 150 Ом | 1.5 кОм | 15 кОм | 150 кОм | 1.5 МОм | 15 МОм |
| 2.2 Ом | 22 Ом | 220 Ом | 2.2 кОм | 22 кОм | 220 кОм | 2.2 МОм | 22 МОм |
| 3.3 Ом | 33 Ом | 330 Ом | 3.3 кОм | 33 кОм | 330 кОм | 3.3 МОм | 33 МОм |
| 4.7 Ом | 47 Ом | 470 Ом | 4.7 кОм | 47 кОм | 470 кОм | 4.7 МОм | 47 МОм |
| 6.8 Ом | 68 Ом | 680 Ом | 6.8 кОм | 68 кОм | 680 кОм | 6.8 МОм | 68 МОм |






























