Закон кулона

Решение практических задач

Два одинаковых шара, один из которых имеет электрический заряд, приводятся в соприкосновение. Расстояние между предметами становится равным 15 см. Известно, что заряженное тело воздействует на незаряженный шар с отталкивающей силой F = 1 мН. Требуется определить первоначальный заряд активного шарика.

При контакте шаров электрический заряд разделяется пополам. По данной величине силы отталкивания определяется заряженность обоих предметов. Преобразование формулы Кулона даёт математическое выражение q2= (F ∙ r2) ∕ k.

Не может не внушать глубокого уважения жизнь, посвящённая служению Отечеству. Но особое восхищение вызывает труд, направленный на углубление знания человечества о законах природы. На I Международном электрическом конгрессе, который проходил 1881 году в Париже, единицам электротехнических измерений присвоили фамилии учёных, открывших их. Кулон возглавляет список.

Все формулы по физике для подготовки к ЦТ

В школьном курсе физике более двухсот формул! Но ведь многие из них легко ( часто в одно два действия) выводятся друг из друга, да и ВСЕ они так уж ли важны и актуальны для успешной сдачи экзамена? Вероятно нет

≈160

К каждой формуле есть пояснение, для многих есть ссылка на развернутое объяснение и примеры и, на десерт, – в удобной компактной форме.

КАК ПОЛЬЗОВАТЬСЯ СПРАВОЧНИКОМ

Главная особенность справочника формул – это ДВА ФИЛЬТРА (две группы кнопок серого цвета).

Первый фильтр называется “ТЕМЫ” , кликая по кнопке с названием темы вы можете быстро отобрать формулы соответсвующей темы. Фильтр работает по принципу исключения т.е. выбирая какую-либо одну тему , вы исключаете другие.

Второй фильтр называется “ВАЖНОСТЬ” , он содержит три кнопки :

– “100 главных формул”. Как следует из названия он позволяет отобрать 100 наиболее важных формул (топ 100 главных формул школьного курса физики).

– “Доп

формулы” – это формулы второго уровня важности, большинство из них выводятся и первой группы, а те что не выводятся более или менее второстепенны

– “третий уровень” – это формулы частные случаи, работающие для узкого круга задач (например формула отклонения луча призмой) , либо формулы появление на ЦТ которых маловероятно.

Фильтр важности работает по принципу дополнения т.е. нажав кнопку “100 главных формул” – отфильтруются 100 основных формул, затем нажав кнопку “Доп

формулы” к предыдущим формулам добавятся формулы второго уровня важности и т.д.

ЦВЕТОВОЙ КОД

Возможно вы уже заметили, что многие формулы раскрашены разными цветами. ЭТО НЕ ДЛЯ КРАСОТЫ (хотя и для нее то же), это способ показать, что с чем соотносится. Например, если в формуле вы видите букву F синего цвета и на рисунке вектор (стрелку) синего цвета, значить эта F характеризует этот вектор. Впрочем смотрите сами, я надеюсь разберетесь

К КАЖДОЙ ФОРМУЛЕ ЕСТЬ ПОЯСНЕНИЕ, что бы его увидеть КЛИКНИТЕ ПО ФОРМУЛЕ !

Для пользователе мобильных устройств. Что бы увидеть описание нужен ДВОЙНОЙ ТАП по экрану (двойное касание к экрану) для большинства формул есть поясняющий рисунок, для многих формул (пока в рамках механики) есть ссылка на развернутое объяснение, примеры или конспект

Так же многие формулы я снабдил информацией о том, на что следует обратить внимание, при работе с этой формулой

В конце списка формул присутствует форма обратной связи, если вы считаете что какой-то формулы не хватает, или хотите предложить как можно улучшить справочник – пишите! Ну и не забывайте делится этой информацией в соцсетях (значки справа вверху экрана).

СМОТРИТЕ ТАК ЖЕ

01.КИНЕМАТИКА

Проекция перемещения через координаты. Средняя скорость (пути). Средняя скорость перемещения. Уравнение координаты для равноПеременного движении (в т.ч. для равномерного движения) Проекция перемещения при равнопеременном движении. Проекция скорости при равнопеременном движении. Уравнение квадратов скоростей. Частота вращения. Линейная скорость при “равномерном” движении по окружности. Угловая скорость вращения. Связь линейной и угловой скорости (при равномерном движении по окружности). Центростремительное ускорение. Закон сложения скоростей (закон сложения перемещений). Горизонтальный бросок – Проекции вектора скорости на оси OX и OY. Горизонтальный бросок – скорость тела. Горизонтальный бросок – время падения. Горизонтальный бросок – дальность полета. Горизонтальный бросок – направление вектора скорости в произвольный момент времени.

ТРЕНАЖЕР ДЛЯ САМОПРОВЕРКИ ФОРМУЛ ПО ФИЗИКЕ. (Список ВСЕХ формул по физике для самопроверки и подготовки к ЦТ 2020)

Примечания

1. Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2004. — Т. III. Электричество. — С. 17. — 656 с. — ISBN 5-9221-0227-3.
2. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: Учеб. пособ.: Для вузов. В 10 т. Т. 2 Теория поля. — 8-е изд., стереот. — М.: ФИЗМАТЛИТ, 2001. — 536 с. — ISBN 5-9221-0056-4 (Т. 2), Гл. 5 Постоянное электромагнитное поле, п. 38 Поле равномерно движущегося заряда, с 132
3. Ландсберг Г. С. Элементарный учебник физики. Том II. Электричество и магнетизм. — М.: Наука, 1964. — Тираж 100 000 экз. — С. 33
4. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: Учеб. пособ.: Для вузов. В 10 т. Т. 3. Квантовая механика (нерелятивистская теория). — 5-е изд., стереот. — М.: Физматлит, 2002. — 808 с. — ISBN 5-9221-0057-2 (Т. 3), гл. 3 Уравнение Шредингера, п. 17 Уравнение Шредингера, с. 74
5. Бете Х. Квантовая механика. — пер. с англ., под ред. В. Л. Бонч-Бруевича, «Мир», М., 1965, Часть 1 Теория строения атома, Гл. 1 Уравнение Шредингера и приближённые методы его решения, с. 11
6. Пайерлс Р. Е.  Законы природы. пер. с англ. под ред. проф. Халатникова И. М. , Государственное издательство физико-математической литературы, М., 1959, тир. 20000 экз., 339 с., Гл. 9 «Электроны при высоких скоростях», п. «Силы при больших скоростях. Другие трудности», c. 263
7. Novi Comm. Acad. Sc. Imp. Petropolitanae, v. IV, 1758, p. 301.
8. J. Priestley. The History and present state of Electricity with original experiments. London, 1767, p. 732.
9. Уиттекер Э. История теории эфира и электричества. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 76. — 512 с. — ISBN 5-93972-070-6.
10. Филонович С. Р. Кавендиш, Кулон и электростатика, М.: Знание. 1988, ББК 22.33 Ф53, гл. «Судьба закона», с. 48
11. Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 4 «Электростатика», п. 1 «Статика», с. 70-71;
12. Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 5 «Применения закона Гаусса», п. 10 «Поле внутри полости проводника», с. 106—108;
13. Калашников С. Г.,
    Электричество, М., ГИТТЛ, 1956, гл. III «Разность потенциалов», п. 34 «Точная проверка закона Кулона», с. 68—69; «Добавления», 1. «Теория опытов Кавендиша и Максвелла», с. 642—645;
14. E. R. Williams, J. E. Faller, H. A. Hill «New Experimental Test of Coulomb’s Law: A Laboratory Upper Limit on the Photon Rest Mass», Phys. Rev. Lett. 26, 721—724 (1971);
15. W. E. Lamb, R. C. Retherford. Fine Structure of the Hydrogen Atom by a Microwave Method (англ.) // Physical Review. — Т. 72, № 3. — С. 241-243.
16. ↑ Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 5 «Применения закона Гаусса», п. 8 «Точен ли закон Кулона?», с. 103;
17. Берестецкий, В. Б., Лифшиц, Е. М., Питаевский, Л. П. Квантовая электродинамика. — Издание 3-е, исправленное. — М.: Наука, 1989. — С. 565-567. — 720 с. — («Теоретическая физика», том IV). — ISBN 5-02-014422-3.
18. Окунь Л. Б. Физика элементарных частиц. Изд. 3-е, М.: «Едиториал УРСС», 2005, ISBN 5-354-01085-3, ББК 22.382 22.315 22.3о, гл. 2 «Гравитация. Электродинамика», «Поляризация вакуума», с. 26-27;
19. «Физика микромира», гл. ред. Д. В. Ширков, М., «Советская энциклопедия», 1980, 528 с., илл., 530.1(03), Ф50, ст. «Эффективный заряд», авт. ст. Д. В. Ширков, стр. 496;
20. Яворский Б. М. «Справочник по физике для инженеров и студентов вузов» / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев, 8-e изд., перераб. и испр., М.: ООО «Издательство Оникс», ООО «Издательство Мир и образование», 2006, 1056 стр.: илл., ISBN 5-488-00330-4 (ООО «Издательство Оникс»), ISBN 5-94666-260-0 (ООО «Издательство Мир и образование»), ISBN 985-13-5975-0 (ООО «Харвест»), УДК 530(035) ББК 22.3, Я22, «Приложения», «Фундаментальные физические постоянные», с. 1008;
21. Uehling E. A ., Phys. Rev., 48, 55, (1935)
22. Швебер С., Бете Г., Гофман Ф. Мезоны и поля. Том 1 Поля гл. 5 Свойства уравнения Дирака п. 2. Состояния с отрицательной энергией c. 56, гл. 21 Перенормировка, п. 5 Поляризация вакуума с 336
23. Мигдал А. Б. Поляризация вакуума в сильных полях и пионная конденсация// Успехи физических наук Т. 123— в. 3.— 1977 г., ноябрь.— с. 369—403;
24. Спиридонов О. П. Универсальные физические постоянные.— М.: Просвещение.— 1984.— с. 52-53;

Устройство крутильных весов Шарля Кулона

Для экспериментов Кулон использовал так называемые «крутильные весы».Их основа — шелковая нить (в безвоздушном пространстве).На нем есть уравновешенный рычаг, по краям которого они нагружены (аналогично помещены в вакуум).Когда возникает внешняя движущая сила, рычаг перемещается горизонтально. И он движется, пока не уравновесится упругой силой существующей шелковой нити.В этом случае рычаг отклоняется от оси (обозначена d). И зная это отклонение, можно вычислить момент кулоновского взаимодействия.допускается замена провода на любой другой материал, главное рассчитать его обратное сопротивление, которое уравновешивает всю конструкцию.

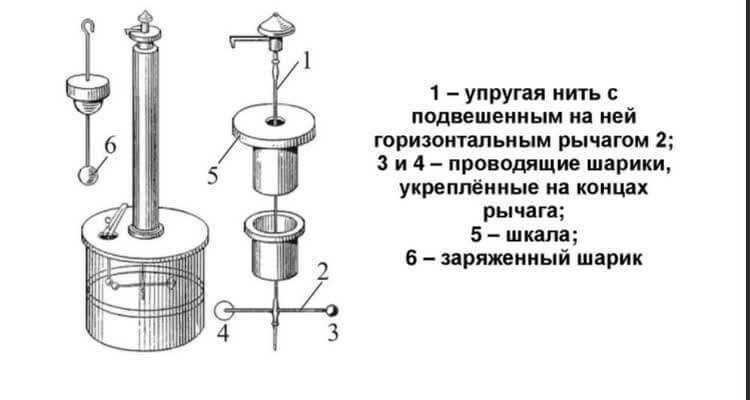
Но это современная вариация весов.Сам Шарль Кулон провел эксперимент иначе.Сначала фиксировалось положение горизонтального рычага, когда оба корпуса не были нагружены.Итак, один из шаров получил определенный заряд. Вернувшись в пустоту, тела начали взаимодействовать друг с другом.С какой силой — показал только шкалу прогиба (с поправкой на силу упругости проволоки, которая поддерживала всю конструкцию).Это физическое явление позволило определить, что сила прямо пропорциональна заряду.Чем больше потенциал тел, тем больше отклонение на шкале.Впоследствии аналогичный эксперимент был проведен в условиях воздуха.Разница в результатах минимальна, поэтому принято считать, что закон Кулона справедлив как для вакуума, так и для воздуха (из-за одинаковой диэлектрической проводимости пространства на единицу).Таким образом, эксперимент Чарльза достаточно реалистичен, чтобы его можно было повторить дома при наличии источника тока и высокоточного измерительного прибора (мультиметра).В качестве тел можно использовать все те же металлические шарики.

Опыт Кулона

Необходимость проведения экспериментов Кулона была вызвана тем, что в середине XVIII в. накопилось много качественных данных об электрических явлениях. Возникла потребность дать им количественную интерпретацию. Поскольку силы электрического взаимодействия были относительно невелики, возникла серьезная проблема в создании метода, который позволил бы произвести замеры и получить необходимый количественный материал.

Французский инженер и ученый Ш. Кулон предложил метод измерения малых сил, который основывался на следующем экспериментальном факте, обнаруженном самим ученым: сила, возникающая при упругой деформации металлической проволоки, прямо пропорциональна углу закручивания, четвертой степени диаметра проволоки и обратно пропорциональна ее длине:

\(~F_{ynp} = k \cdot \dfrac{d^4}{l} \cdot \varphi\) ,

где d

– диаметр,l – длина проволоки,φ – угол закручивания. В приведенном математическом выражении коэффициент пропорциональностиk находился опытным путем и зависел от природы материала, из которого изготавливалась проволока.

Данная закономерность была использована в так называемых крутильных весах. Созданные весы позволили измерить ничтожно малые силы порядка 5·10-8 Н.

Рис. 3

Крутильные весы (рис. 3, а) состояли из легкого стеклянного коромысла 9

длиной 10,83 см, подвешенного на серебряной проволоке5 длиной около 75 см, диаметром 0,22 см. На одном конце коромысла располагался позолоченный бузиновый шарик8 , а на другом – противовес6 – бумажный кружок, смоченный в скипидаре. Верхний конец проволоки прикреплялся к головке прибора1 . Здесь же имелся указатель2 , с помощью которого отсчитывался угол закручивания нити по круговой шкале3 . Шкала была проградуирована. Вся эта система размещалась в стеклянных цилиндрах4 и11 . В верхней крышке нижнего цилиндра имелось отверстие, в которое вставлялась стеклянная палочка с шариком7 на конце. В опытах применялись шарики с диаметрами в пределах 0,45 – 0,68 см.

Перед началом эксперимента указатель головки устанавливался на нулевой отметке. Затем шарик 7

заряжался от предварительно наэлектризованного шарика12 . При соприкосновении шарика7 с подвижным шариком8 происходило перераспределение заряда. Однако из-за того, что диаметры шариков были одинаковыми, одинаковыми были и заряды на шариках7 и8 .

Вследствие электростатического отталкивания шариков (рис. 3, б) коромысло 9

поворачивалось на некоторый уголγ (по шкале10 ). С помощью головки1 это коромысло возвращалось в исходное положение. По шкале3 указатель2 позволял определять уголα закручивания нити. Общий угол закручивания нитиφ =γ +α . Сила же взаимодействия шариков была пропорциональнаφ , т. е. по углу закручивания можно судить о величине этой силы.

При неизменном расстоянии между шариками (оно фиксировалось по шкале 10

в градусной мере) исследовалась зависимость силы электрического взаимодействия точечных тел от величины заряда на них.

Для определения зависимости силы от заряда шариков Кулон нашел простой и остроумный способ изменения заряда одного из шариков. Для этого он соединял заряженный шарик (шарики 7

или8 ) с таким же по размерам незаряженным (шарик12 на изолирующей ручке). Заряд при этом распределялся поровну между шариками, что и уменьшало исследуемый заряд в 2, 4 и т. д. раз. Новое значение силы при новом значении заряда опять определялось экспериментально. При этом выяснилось,что сила прямо пропорциональна произведению зарядов шариков : \(~F \sim q_1 \cdot q_2\) . Зависимость силы электрического взаимодействия от расстояния была обнаружена следующим образом. После сообщения шарикам заряда (он был у них одинаковый) коромысло отклонялось на некоторый угол γ

. Затем поворотом головки1 уменьшался этот угол доγ 1. Общий угол закручиванияφ 1 =α 1 + (γ –γ 1)(α 1 – угол поворота головки). При уменьшении углового расстояния шариков доγ 2 общий угол закручиванияφ 2 =α 2 + (γ –γ 2) . Было замечено, что, еслиγ 1 = 2γ 2, ТОφ 2 = 4φ 1, т. е. при уменьшении расстояния в 2 раза сила взаимодействия возрастала в 4 раза. Во столько же раз увеличился момент силы, так как при деформации кручения момент силы прямо пропорционален углу закручивания, а значит, и сила (плечо силы оставалось неизменным). Отсюда вытекает вывод:сила взаимодействия двух заряженных шариков обратно пропорциональна квадрату расстояния между ними: \(~F \sim \dfrac{1}{r^2}\) .

Закон Кулона простым языком

С помощью данной закономерности можно описать механизм взаимодействия тел, обладающих зарядом. Закон Кулона является фундаментальным, то есть обладает экспериментальным подтверждением и не был установлен на основе какого-либо природного закона. Формулировка утверждения справедлива для точечных зарядов в вакуумной среде, которые неподвижны. В реальном мире подобная ситуация невозможна. Однако таковыми можно считать заряды, обладающие размерами, существенно меньшими по сравнению с расстоянием между ними. Сила взаимодействия в воздухе практически соизмерима с силой взаимодействия в вакууме и отличается лишь на одну тысячную.

Электрическим зарядом называют физическую величину, определяющуюся свойством частиц или тел вступать в электромагнитные силовые взаимодействия.

Описание механизма взаимного воздействия неподвижных зарядов друг на друга было представлено физиком из Франции Ш. Кулоном в 1785 году. В подтверждение закона были проведены опыты по измерению взаимодействия между шарами с размерами, которые значительно меньше, чем расстояние, на котором они расположены. Подобные тела получили название точечных зарядов. По итогам многочисленных опытов Кулон вывел закон.

Закон Кулона гласит, что сила взаимодействия двух точечных электрических зарядов, расположенных неподвижно, в вакуумной среде прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними. Вектор силы ориентирован вдоль прямой, соединяющей заряды. Данная сила является силой притяжения в случае, когда заряды разноименные, либо силой отталкивания, если заряды одноименные.

Модули зарядов обозначают, как \(|q_1|\) и \(|q_2|\). В этом случае Закон Кулона можно представить в виде уравнения:

\(F=k\times \frac{\left|q1 \right|\times \left|q2 \right|}{r^{2}}\)

Коэффициент пропорциональности k, согласно закону Кулона, определяется выбором системы единиц.

\(k=\frac{1}{4\pi \varepsilon _{0}}\)

Полная формула закона Кулона обладает следующим видом:

\(F=\frac{\left|q1 \right|\times \left|q2 \right|}{4\pi \varepsilon _{0}\varepsilon r^{2}}\)

где \(F\) — Сила Кулона,

\(q_1\) и \(q_2\) являются электрическими зарядами тел;

r — расстояние между зарядами;

\(\varepsilon _{0}\) — электрическая постоянная, равная \(8,85*10^{-12}\);

\(\varepsilon \)  — диэлектрическая проницаемость среды, равная 9*109;

k — коэффициент пропорциональности в законе Кулона.

Силы взаимодействия определяются третьим законом Ньютона:

\(\vec{F}_{12}=\vec{F}_{21}\)

Данные силы представляют собой силы отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках. Для обозначения электрических зарядов используют буквы q и Q. Благодаря имеющимся фактам, полученным в результате экспериментов, можно сделать следующие выводы:

1. Имеется два типа электрических зарядов, которые условно обозначают положительными и отрицательными.
2. Допускается передача заряда от одного объекта к другому, так как в отличие от массы, не принадлежат к категории неотъемлемых характеристик тела, поэтому один и тот же объект при разных обстоятельствах может обладать как положительным, так и отрицательным зарядом.
3. Одноименные заряды будут отталкиваться, а разноименные — притягиваться, что подтверждает принципиальную разницу между электромагнитными и гравитационными силами, ведь, благодаря гравитации тела в любом случае притягиваются друг к другу.

Электрическое или кулоновское взаимодействие называют взаимодействием неподвижных электрических зарядов. Существует специальный раздел в электродинамике под названием электростатика, целью которого является изучение кулоновского взаимодействия. Справедливое утверждение закона Кулона распространяется на точечные заряженные тела. В случае когда размеры зарядов намного меньше, чем расстояние между ними, закон Кулона действует на практике. Для его выполнения необходимо соблюдать несколько важных условий:

• точечность зарядов;
• неподвижность зарядов;
• взаимодействие зарядов в вакууме.

Кулоном называют заряд, который проходит за 1 секунду через поперечное сечение проводника при силе тока 1 Ампер.

Единица силы тока — Ампер — относится к основным единицам измерения таким, как длина, время, масса. В Международной системе СИ принято использовать в качестве единицы заряда кулон (Кл).

Взаимодействие разноименных и одноименных электрических зарядов

Электростатические силы отталкивания принято считать положительными, силы притяжения – отрицательными. Знаки сил взаимодействия соответствуют закону Кулона: произведение одноимённых зарядов является положительным числом, и сила отталкивания имеет положительный знак. Произведение разноимённых зарядов является отрицательным числом, что соответствует знаку силы притяжения.

В опытах Кулона измерялись силы взаимодействия заряженных шаров, для чего применялись крутильные весы. На тонкой серебряной нити подвешена лёгкая стеклянная палочка с, на одном конце которой закреплён металлический шарик а, а на другом противовес d. Верхний конец нити закреплён на вращающейся головке прибора е, угол поворота которой можно точно отсчитывать. Внутри прибора имеется такого же размера металлический шарик b, неподвижно закреплённый на крышке весов. Все части прибора помещены в стеклянный цилиндр, на поверхности которого нанесена шкала, позволяющая определить расстояние между шариками a и b при различных их положениях.

При сообщении шарикам одноимённых зарядов они отталкиваются друг от друга. При этом упругую нить закручивают на некоторый угол, чтобы удержать шарики на фиксированном расстоянии. По углу закручивания нити и определяют силу взаимодействия шариков в зависимости от расстояния между ними. Зависимость силы взаимодействия от величины зарядов можно установить так: сообщить каждому из шариков некоторый заряд, установить их на определённом расстоянии и измерить угол закручивания нити. Затем надо коснуться одного из шариков таким же по величине заряженным шариком, изменяя при этом его заряд, так как при соприкосновении равных по величине тел заряд распределяется между ними поровну. Для сохранения между шариками прежнего расстояния необходимо изменить угол закручивания нити, а, следовательно, и определить новое значение силы взаимодействия при новом заряде.

Диэлектрики в электрическом поле

Закон Кулона и связь с гравитацией

Мы уже упоминали Шарля Кулона. В честь него названа единица измерения заряда — Кулон. Он придумал закон о взаимодействии зарядом.

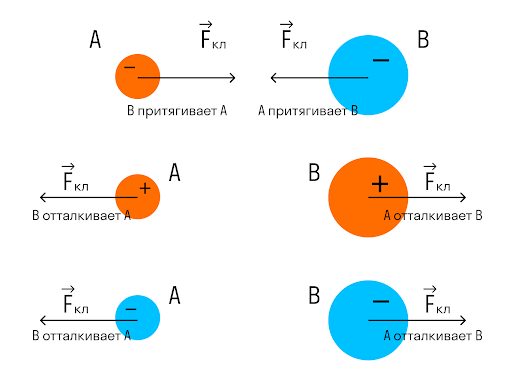
Мы уже знаем, что заряды бывают положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные — притягиваются. Это значит, что сила направлена туда же, куда заряд будет стремиться двигаться.

Например, у положительного заряда сила будет направлена в сторону отрицательного, если он есть где-то поблизости, и от положительного, так как одноименные заряды отталкиваются.

Согласно третьему закону Ньютона, силы одной природы возникают попарно, равны по величине, противоположны по направлению. Если взаимодействуют два неодинаковых заряда, сила, с которой больший заряд действует на меньший (В на А) равна силе, с которой меньший действует на больший (А на В).

Интересно, что у различных законов физики есть некоторые общие черты. Вспомним закон тяготения. Сила гравитации также обратно пропорциональны квадрату расстояния, но уже между массами. И невольно возникает мысль, что в этой закономерности таится глубокий смысл. До сих пор никому не удалось представить тяготение и электричество, как два разных проявления одной и той же сущности.

Сила и тут изменяется обратно пропорционально квадрату расстояния, но разница в величине электрических сил и сил тяготения поразительна. Пытаясь установить общую природу тяготения и электричества, мы обнаруживаем такое превосходство электрических сил над силами тяготения, что трудно поверить, будто у тех и у других один и тот же источник. Нельзя говорить, что одно действует сильнее другого, ведь все зависит от того, какова масса и каков заряд.

Рассуждая о том, насколько сильно действует тяготение, мы не вправе говорить: «Возьмем массу такой-то величины», потому что мы выбираем ее сами. Но если мы возьмем то, что предлагает нам сама Природа: ее собственные числа и меры, которые не имеют ничего общего с нашими дюймами, годами — с любыми нашими мерами, вот тогда мы можем сравнивать.

Мы возьмем элементарную заряженную частицу, например, электрон. Две элементарные частицы, два электрона, за счет электрического заряда отталкивают друг друга с силой, обратно пропорциональной квадрату расстояния между ними, а за счет гравитации притягиваются друг к другу опять-таки с силой, обратно пропорциональной квадрату расстояния.

Тяготение относится к электрическому отталкиванию, как единица к числу с 42 нулями. Да, это огромное число! Исследователи перебирали все большие числа, чтобы понять — откуда это взялось. Одно из таких больших чисел — это отношение диаметра Вселенной к диаметру протона — как ни удивительно, это тоже число с 42 нулями. Нормально так перебрали.

Если вы смотрели Рика и Морти, то знаете о теории параллельных вселенных и о том, что эти вселенные расширяются. Из-за расширения вселенной постоянная сила тяготения меняется. Хотя эта гипотеза еще не опровергнута, у нас нет никаких свидетельств в ее пользу. Наоборот, некоторые данные говорят о том, что постоянная сила тяготения не менялась таким образом. Это громадное число по сей день остается загадкой.

От расширяющихся вселенных и мультиков перейдем к чему-то более приземленному — к задачам.

Задачка раз

Расстояние между двумя точечными электрическими зарядами уменьшили в 3 раза, каждый из зарядов увеличили в 3 раза. Во сколько раз увеличился модуль сил электростатического взаимодействия между ними?

Решение:

Возьмем закон Кулона.

F = k*(q₁*q₂/r²)

Если расстояние уменьшилось в 3 раза, то знаменатель уменьшился в 9 раз. Каждый из зарядов увеличился в три раза, значит числитель увеличился в 9 раз. Уменьшаем знаменатель в 9 раз, тем самым увеличивая всю дробь в 9 раз, увеличиваем числитель в 9 раз, получаем, что вся дробь увеличилась в 81 раз. И это ответ.

Ответ: модуль сил электростатического взаимодействия увеличится в 81 раз.

Задачка два (последняя!)

Два одинаковых маленьких отрицательно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 5 раз.

Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₂ к F₁.

Решение:

Для начала найдем заряд шариков после соприкосновения.

(q₁ + q₂)/2= (5q + q)/2= 3q

Теперь по закону кулона найдем силу F2

F = k * (q₁*q₂/r²) = (9kq²)/r²

И находим отношение сил

F₂/F₁ = 1,8

Ответ: отношение сил равно 1,8