Векторные диаграммы в электротехнике

Подготовка данных для лучевой диаграммы

Как уже упоминалось выше данный шаблон будет обладать возможностью визуального построения связей до 20-ти участников (компаний, филиалов, контрагентов и т.п.). На листе книги шаблона «Данные» предоставленная таблица для заполнения входящих значений. Например, заполним ее для 14-ти участников рынка:

На этом же листе создадим дополнительную таблицу, которая представляет собой матрицу связей всех возможных участников, сгенерированную формулой:

С подготовкой данных мы закончили переходим к обработке.

Как вычислить сумму векторов?

Вектора и матрицы в электронной таблице хранятся в виде массивов.

Известно, что сумма векторов – это вектор, координаты которого равны суммам соответствующих координат исходных векторов:

Для вычисления суммы векторов нужно выполнить следующую последовательность действий:

– В диапазоны ячеек одинаковой размерности ввести значения числовых элементов каждого вектора.

– Выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходные векторы.

– Ввести в выделенный диапазон формулу перемножения диапазонов

– = Адрес_Вектора_1 + Адрес_Адрес_Вектора_2

– Нажать комбинацию клавиш + +.

Пример.

Даны два вектора:

Требуется вычислить сумму этих векторов.

Решение:

– В ячейки диапазона А2:A4

введем значения координат вектора a1, а в ячейки диапазонаС2:С4 – координаты вектора a2.

– Выделим ячейки диапазона, в которых будет вычисляться результирующий вектор С (E2:E4

) и введем в выделенный диапазон формулу:

=A2:A4+C2:C4

– Нажмем комбинацию клавиш + +. В ячейках диапазона E2:E4

будут вычислены соответствующие координаты результирующего вектора.

Построение круговой диаграммы по результатам опытов холостого хода и короткого замыкания

Круговую диаграмму цепи можно построить по показаниям приборов, измерив те величины, которые являются исходными при построении.

Неразветвленная цепь

В неразветвленных цепях, изображенных на рис. 19.1, а; 19.4, а, б, достаточно измерить напряжение и ток I_к при коротком замыкании между точками 2 и 2′ (рис. 19.9, а, б).

Величина постоянного сопротивления определяется по показаниям приборов, отношение напряжения к току равно Х_L в схеме рис. 19.9, а и R — в схеме рис. 19.9, б.

Рис. 19.9. К вопросу построения круговой диаграммы неразветвленной цепи по результатам опытов

В схеме рис. 19.5, а нужно дополнительно измерить активную мощность при коротком замыкании (рис. 19.9, в).
По показаниям приборов определяют параметры катушки:

Разветвленная цепь

Для построения круговой диаграммы разветвленной цепи требуется провести опыты холостого хода и короткого замыкания (рис. 19.10).
При холостом ходе (разрыв цепи между точками 2 и 2′) измеряют ток I₁, мощность Р₁ первой ветви и общее напряжение U. Определяют
При коротком замыкании между точками 2 и 2′ измеряют ток I_к, мощность Р_к всей цепи и общее напряжение U. Определяют
Этих данных достаточно для построения круговой диаграммы токов.

Рис. 19.10. К вопросу о построении круговой диаграммы разветвленной цепи по результатам опытов

Задача 19.7.

Построить круговую диаграмму цепи рис. 19.11, а по результатам опытов холостого хода и короткого замыкания:
Пользуясь круговой диаграммой, построить кривые зависимости тока, активной, реактивной мощностей и от сопротивления конденсатора Х_С.Решение. По показаниям приборов определим коэффициенты мощности первой ветви (холостой ход) и всей цепи при коротком замыкании участка 2-2′:
Для того чтобы не пользоваться транспортиром при построении круговой диаграммы, можно определить активную и реактивную составляющие тока: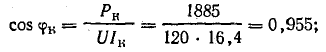

Круговую диаграмму (рис. 19.11, б) рекомендуется построить на листе миллиметровой бумаги в следующем порядке.

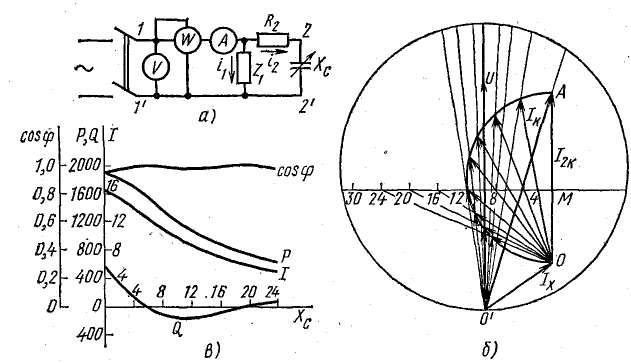
Рис. 19.11. К задаче 19.7

Выбрать масштабы тока и напряжения (например, ; ) и отложить на чертеже векторы: U — в произвольном направлении, активные составляющие токов — вдоль вектора напряжения, реактивные — перпендикулярно ему, учитывая их индуктивный характер.
Построив векторы токов I_х и I_к, провести вектор I_2к так, чтобы
На векторе I_2к (отрезок ), как на диаметре, построить полуокружность токов слева от диаметра , учитывая емкостный характер тока I₂. Из диаграммы следует, что
Активное сопротивление во второй ветви
Далее надо выбрать масштаб сопротивлений {например, М_R = 4 Ом/см) и отложить от точки О по направлению вектора тока I_2к величину активного сопротивления R₂ (отрезок ). Через точку М провести линию реактивных сопротивлений и нанести шкалу.
Величины, определенные по круговой диаграмме согласно условию задачи, записаны в табл. 19.2.

Таблица 19.2

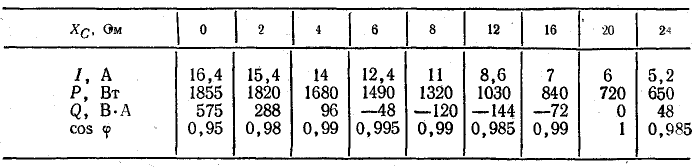
При Х_С = 5 Ом, Х_С = 20 Ом в цепи имеет место резонанс токов. Это видно из круговой диаграммы. Ток I совпадает по фазе с напряжением. На рис. 19.11, в построены графики согласно условию задачи.

Diagrams.net

Это бесплатный онлайн-редактор диаграмм. С его помощью можете создавать высококачественные проекты, настраиваемые блок-схемы, сложные сетевые диаграммы и макеты системы на унифицированном языке моделирования. Все, что нужно сделать, чтобы начать использовать программу, — зайти на сайт Diagrams.net, выбрать, где хранить свои работы и приступить к проектированию.

Интерфейс оформлен просто, поэтому можно быстро найти популярные формы, функции и настройки. Шаблонов для построения диаграмм не так много, как у конкурентов, зато платформа максимально проста в использовании и бесплатна.

Особенности Draw.io:

Готовые диаграммы можно сохранять в форматах JPEG, PNG и SVG.
Возможность делиться файлом с другими для совместного редактирования.
Десятки разных макетов для построения диаграммы.
Бесплатное использование.
Интеграция с Google Drive.

Построение векторной диаграммы

В основе метода векторных диаграмм лежит тот факт, что любую меняющуюся величину, которая изменяется по синусоидальному закону определяется, как проекция на выбранное направление вектора, вращающийся вокруг своей начальной скорости, равной угловой частоте колебаний изображаемой переменной величины.

Определение 2

Угловая скорость – это векторная величина, которая характеризует направление и быстроту вращения материальной точки вокруг центра вращения.

Рассмотрим электрическую цепь, которая состоит из последовательно соединенных резистора, источника тока, конденсатора и индуктивности. Схема данной цепи изображена на рисунке ниже.

Схема электрической цепи. Автор24 — интернет-биржа студенческих работ» />Рисунок 1. Схема электрической цепи. Автор24 — интернет-биржа студенческих работ

Здесь U — мгновенное значение переменного напряжения; i — электрический ток в настоящий момент времени.

Изменение мгновенного значения переменного напряжения можно рассчитать по следующей формуле:

$i=Im Coswt$

По закону сохранения заряда ток имеет одно и тоже значение в любой момент времени. Таким образом, на каждом элементе электрической цепи будет падать напряжение:

UL на индуктивности.
UR на активном сопротивлении.
UC на конденсаторе.

По второму правилу Кирхгофа напряжение источника тока равно:

$U=UC + UL + UR$

По второму закону Ома:

$I = U / R$

Откуда,

$U = I • R$

Для активного сопротивления значение R зависит от свойств проводника (не зависит от момента времени, электрического тока), поэтому оно совпадает с напряжением по фазе, таким образом:

$UR = Im • R • Coswt.$

Конденсатор в электрической цепи переменного тока обладает емкостным реактивным сопротивлением, а напряжение на конденсаторе отстает по фазе от тока на П/2, поэтому:

Рисунок 2. Уравнение. Автор24 — интернет-биржа студенческих работ

Напряжение на катушке индуктивности опережает ток по фазе на величину П/2, поэтому

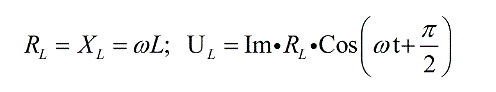Рисунок 3. Уравнение. Автор24 — интернет-биржа студенческих работ

Получается, что сумму падения напряжений можно вычислить по следующей формуле:

$U = Um • Cos(wt+ф)$

По закону сохранения заряда ток всегда одинаков во всех частях, таким образом векторная диаграмма токов будет иметь следующий вид:

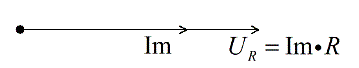Рисунок 4. Векторная диаграмма токов. Автор24 — интернет-биржа студенческих работ

Im — амплитудное значение электрического тока.

Напряжение (на активном сопротивлении) совпадает с током по фазе, поэтому их векторы будут сонаправлены и откладываются из одной точки

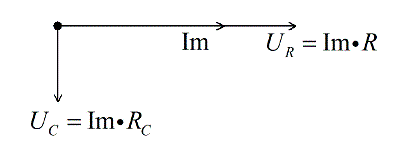Рисунок 5. Векторная диаграмма. Автор24 — интернет-биржа студенческих работ

Так как напряжение на конденсаторе отстает от электрического тока на величину П/2, то его вектор должен быть отложен под прямым углом вниз, перпендикулярно по отношению к вектору напряжения на активном сопротивлении.

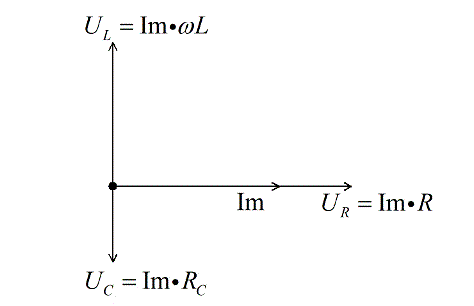Рисунок 6. Векторная диаграмма. Автор24 — интернет-биржа студенческих работ

Напряжение на катушке индуктивности опережает ток на П/2, поэтому его вектор откладывается под прямым углом вверх, перпендикулярно вектору напряжения на активном сопротивлении.

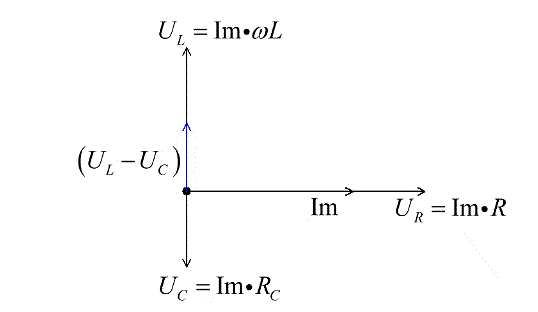Рисунок 7. Векторная диаграмма. Автор24 — интернет-биржа студенческих работ

Складываем векторы напряжений на активных элементах цепи и получаем разницу (принимаем, что UL>UC), которая будет направлена вверх.

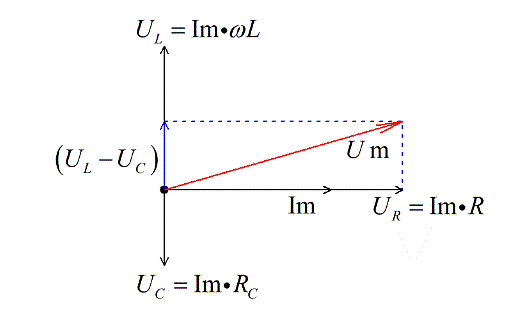Рисунок 8. Векторная диаграмма. Автор24 — интернет-биржа студенческих работ

Затем прибавляем вектор напряжения на активном сопротивлении, и получаем вектор суммарного напряжения (по правилу векторного сложения).

Рисунок 9. Векторная диаграмма. Автор24 — интернет-биржа студенческих работ

Затем по закону Ома и Теореме Пифагора, получаем формулу для расчета амплитудного значения тока:

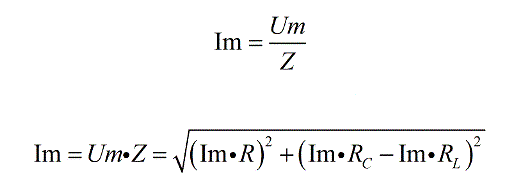Рисунок 10. Формула. Автор24 — интернет-биржа студенческих работ

где, Z — сопротивление общее сопротивление.

Затем, преобразуя данное уравнение получаем формулу для расчета полного сопротивления

Рисунок 11. Формула. Автор24 — интернет-биржа студенческих работ

Разновидности векторных диаграмм

Для корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика. Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось.

С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии.

Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов.

Круговая диаграмма

Допустим, что надо изучить изменение параметров тока в цепи при разных значениях сопротивления резистора в диапазоне от нуля до бесконечности. В этой схеме напряжение на выходе (U) будет равно сумме значений (UR и UL) на каждом из элементов. Индуктивный характер второй величины подразумевает перпендикулярное взаимное расположение, что хорошо видно на части рисунка б). Образованные треугольники отлично вписываются в сегмент окружности 180 градусов. Эта кривая соответствует всем возможным точкам, через которые проходит конец вектора UR при соответствующем изменении электрического сопротивления. Вторая диаграмма в) демонстрирует отставание тока по фазе на угол 90°.

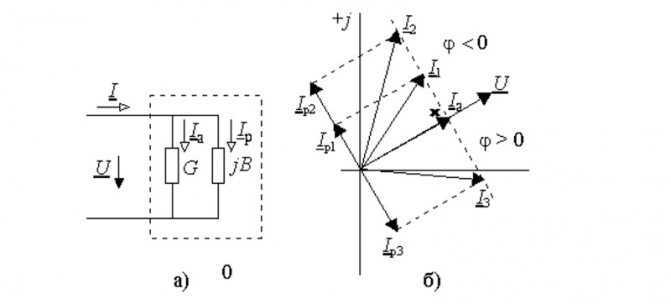
Линейная диаграмма

Здесь изображен двухполюсный элемент с активной и реактивной составляющими проводимости (G и jB, соответственно). Аналогичными параметрами обладает классический колебательный контур, созданный с применением параллельной схемы. Отмеченные выше параметры можно изобразить векторами, которые расположены постоянно под углом 90°. Изменение реактивной компоненты сопровождается перемещением вектора тока (I1…I3). Образованная линия располагается перпендикулярно U и на расстоянии Ia от нулевой точки оси координат.

Как сделать лучевую векторную диаграмму связей в Excel

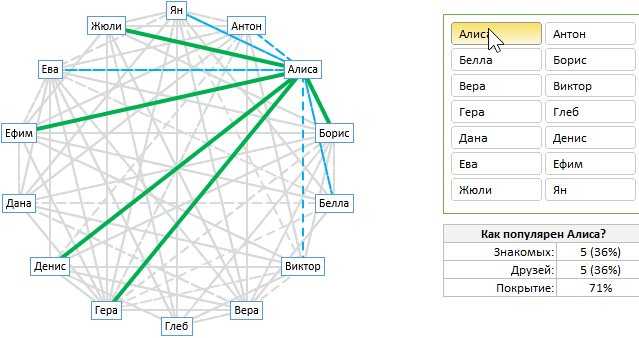
Сначала взглянем на то, что мы пытаемся построить и визуально оценим объем работы. Выглядит интересно? Тогда читайте дальше, чтобы узнать, как это создать.

Чтобы создать лучевую диаграмму в Excel для визуального анализа взаимоотношений в сети, нам нужно сначала понять ее различные составляющие.

Как видите, диаграмма содержит следующие части:

Набор точек, каждая из которых представляет одну заинтересованную сторону – участники сети.
Набор сероватых толстых сплошных и тонких пунктирных линий, представляющих все отношения между людьми. Сплошные – сильные связи (например, друзья), пунктирные – слабые связи (знакомые).
Набор зеленых толстых и синих пунктирных линий, представляющих отношения для выбранного конкретного участника сетевой группы.
Срез для выбора анализа участника – как панель управления лучевой диаграммой.
Табличка со сводной статистикой выбранного человека.

Векторные диаграммы при последовательном и параллельном соединении элементов

Для построения векторных диаграмм сначала составляются уравнения по законам Кирхгофа для исследуемой цепи. Пример рассматриваемой цепи изображен на рисунке ниже.

Рисунок 2. Цепь. Автор24 — интернет-биржа студенческих работ

Для вышепредставленной цепи, по второму закону Кирхгофа уравнение будет выглядеть следующим образом:

$E = Ur + UL + Uc$

По закону Ома падения напряжения на каждом элемента можно выразить следующим образом:

$Ur = I • R$

$ULl = I • jXL$

$Uc = — I • jXc$

Отсюда следует, что для построения векторной диаграммы необходимо отобразить слагаемые уравнения в комплексной плоскости. Поэтому при построении векторной диаграммы умножение вектора на мнимую единицу j становится причиной поворота вектора на 90 градусов против часовой стрелки, а умножение на — j к повороту по часовой стрелке на 90 градусов. Падение напряжения на резисторе (Ur) совпадает с током I (так как $U = I • R$). Падение напряжения на индуктивном сопротивлении опережает на 90 градусов вектор тока (так как $Ul = I • jXL$), а напряжение емкостном напряжения отстает от вектора тока на 90 градусов($Uc = — I • jXc$), таким образом векторная диаграмма будет выглядеть следующим образом.

Рисунок 3. Векторная диаграмма. Автор24 — интернет-биржа студенческих работ

Рассмотрим электрическую цепь с параллельным соединением, представленную на рисунке ниже.

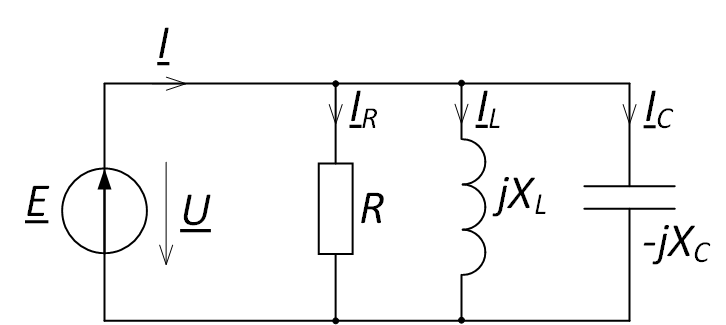Рисунок 4. Цепь с параллельным соединением. Автор24 — интернет-биржа студенческих работ

Уравнение для данной электрической цепи по первому закону Кирхгофа будет иметь следующий вид:

$I – Ir – Ic — IL = 0$

Откуда

$I = Ir + IL + Ic = 0$

Затем определяем токи в ветвях по закону Ома, учитывая, что –j = 1 / j и получаем:

$Ir = E / R$

$IL = E / (jXL) = — j • (E / XL)$

$Ic = E / (- jXc) = j • (E / Xc)$

Приведенные в уравнении слагаемые, также отражаются в комплексной плоскости. При построении векторной диаграммы на комплексной плоскости сначала отображается вектор электродвижущей силы (Е), а затем, уже относительно него отображаются векторы токов, с учетом отношений мнимой величины (j). Ток в резисторе совпадает по направлению с электродвижущей силой (так как $Ir = E / R$, а число R является действительной величиной). В индуктивном сопротивлении ток отстает от электродвижущей силы на 90 градусов (так как $IL = -j • (E / XL$, а величина (-j) представляет собой причину поворота этого вектора на 90 градусов по часовой стрелке). В емкостном сопротивлении ток будет опережать вектор электродвижущей силы на 90 градусов (так как $Ic = j • (E / Xc), умножение на величину j является причиной поворота данного вектора на 90 градусов против часовой стрелки. Результирующий вектор, таким образом, определяется после геометрического сложения векторов, согласно правилу параллелограмма. Получившаяся векторная диаграмма изображена на рисунке ниже. Ic = j • (E / Xc), умножение на величину j является причиной поворота данного вектора на 90 градусов против часовой стрелки. Результирующий вектор, таким образом, определяется после геометрического сложения векторов, согласно правилу параллелограмма. Получившаяся векторная диаграмма изображена на рисунке ниже.

Рисунок 5. Векторная диаграмма. Автор24 — интернет-биржа студенческих работ

Алгоритм построения векторной диаграммы для произвольной электрической цепи аналогичен алгоритму для параллельной цепи, с учетом прикладываемых напряжений и токов, которые протекают в ветвях.

Примеры применения

Допустимый ток для медных проводов — плотность тока в медном проводнике

В следующих разделах приведены описания задач, которые решают с помощью представленной методики. Следует подчеркнуть, что применение комплексных чисел пригодно для сложных расчетов с высокой точностью. Однако на практике достаточно часто сравнительно простой векторной графики с наглядным отображением исходной информации на одном рисунке.

Механика, гармонический осциллятор

Таким термином обозначают устройство, которое можно вывести из равновесного состояния. После этого система возвращается в сторону исходного положения, причем сила (F) соответствующего воздействия зависит от дальности первичного перемещения (d) прямо пропорционально. Величину ее можно уточнить с помощью постоянного корректирующего коэффициента (k). Отмеченные определения связаны формулой F=-d*k

Формулы для расчета основных параметров гармонического осциллятора

К сведению. Аналогичные процессы происходят в системах иной природы. Пример – создание аналога на основе электротехнического колебательного контура (последовательного или параллельного). Формулы остаются теми же с заменой соответствующих параметров.

Свободные гармонические колебания без затухания

Продолжая изучение темы на примерах механических процессов, можно отметить возможность построения двухмерной схемы. Скорость в этом случае на оси Х отображается так же, как и в одномерном варианте. Однако здесь можно учесть дополнительно фактор ускорения, которое направляют под углом 90° к предыдущему вектору.

Гармонический осциллятор с затуханием и внешней вынуждающей силой

В этом случае также можно воспользоваться для изучения взаимного влияния дополнительных факторов векторной графикой. Как и в предыдущем примере, скорость и другие величины представляют в двухмерном виде. Чтобы правильно моделировать процесс, проверяют суммарное воздействие внешних сил. Его направляют к центру системы (точке равновесия). С применением геометрических формул вычисляют амплитуду механических колебаний после начального воздействия с учетом коэффициента затухания и других значимых факторов.

Расчет электрических цепей

Векторную графику применяют для сравнительно несложных цепей, которые созданы из набора элементов линейной категории: конденсаторы, резисторы, катушки индуктивности. Для более сложных схем пользуются методикой расчета «Комплексных амплитуд», в которой реактивные компоненты определяют с помощью импедансов.

Векторная диаграмма для схемы соединений без нейтрального провода – звезда

Векторная диаграмма в данном случае выполняет функцию вспомогательного чертежа, который упрощает решение геометрических задач. Для катушек и конденсаторов, чтобы не пользоваться комплексным исчислением, вводят специальный термин – реактивное сопротивление. При синусоидальном токе изменение напряжения на индуктивном элементе описывается формулой U=-L*w*I0sin(w*t+f0).

Несложно увидеть подобие с классическим законом Ома. Однако в данном примере изменяется фаза. По этому параметру на конденсаторе напряжение отстает от тока на 90°. В индуктивности – обратное распределение. Эти особенности учитывают при размещении векторов на рисунке. В формуле учитывается частота, которая оказывает влияние на величину этого элемента.

Схемы и векторные диаграммы для идеального элемента и диэлектрика с потерями

Преобразование Фурье

Векторные технологии применяют для анализа спектров радиосигналов в определенном диапазоне. Несмотря на простоту методики, она вполне подходит для получения достаточно точных результатов.

Сложение двух синусоидальных колебаний

В ходе изучения таких источников сигналов рекомендуется работать со сравнительно небольшой разницей частот. Это поможет создать график в удобном для пользователя масштабе.

Фурье-образ прямоугольного сигнала

В этом примере оперируют суммой синусоидальных сигналов. Последовательное сложение векторов образует многоугольник, вращающийся вокруг единой точки. Для правильных расчетов следует учитывать отличия непрерывного и дискретного распределения спектра.

Для этого случая пользуются тем же отображением отдельных синусоид в виде векторов, как и в предыдущем примере. Суммарное значение также вписывается в окружность.

Конденсатор в цепи синусоидального тока

Если приложенное к конденсатору напряжение не меняется во времени, то заряд q=CU на одной его обкладке и заряд –q=-Cu на другой (С-ёмкость конденсатора) неизменны и ток через конденсатор не проходит (

). Если же напряжение на конденсаторе меняется во времени, например по синусоидальному закону (2-34)

то по синусоидальному закону будет меняться заряд q конденсатора:

(2-35)

и конденсатор будет периодически перезаряжаться. Периодическая перезарядка конденсатора сопровождается протеканием через него синусоидального тока

(2-36)

Из сопоставления (2-34) и (2-36) видно, что ток через конденсатор опережает по фазе напряжение на конденсаторе на 90º. На векторной диаграмме вектор тока

направлен по вещественной оси комплексной плоскости, а вектор напряжения на конденсаторе направлен в отрицательном направлении мнимой оси.

На рис. 2-16 изображен конденсатор емкостью С, по которому протекает синусоидальный ток

Рис. 2-16. Конденсатор в цепи синусоидального тока

На рис. 2-17 изображена векторная диаграмма при протекании через конденсатор синусоидального тока.

Рис. 2-17. Векторная диаграмма

Таким образом, при протекании синусоидального тока через конденсатор вектор тока

опережает вектор напряжения на конденсаторе на 90º.

Из выражения (2-36) запишем амплитуду тока

(2-37)

Ясно, что выражение в знаменателе есть некоторое сопротивлению согласно закону Ома:

, (2-38)

которое называют емкостным сопротивлением конденсатора.

Проверим размерность Xc:

(2-39)

Таким образом, конденсатор оказывает переменному току сопротивление

. Оно обратно пропорционально угловой частоте ω. (2-40)

Графики мгновенных значений U,I,p приведены на рис. 2-18.

Рис. 2-18. Графики мгновенных значений тока

, напряжения и

Во вторую и все чётные четверти периода мгновенная мощность р положительная, и в этой четверти периода энергия от источника передаётся конденсатору и идёт на создание электрического поля конденсатора.

В первую и все нечётные четверти периода мгновенная мощность р отрицательная, и энергия, занесённая в электрическое поле конденсатора, возвращается источнику.

Мгновенная мощность положительная, когда напряжение

и ток имеют одинаковые знаки, и отрицательная – когда напряжение и ток имеют противоположные знаки.

Мгновенная мощность р равна нулю, когда либо ток

, либо напряжение проходят через нуль. Это происходит каждую четверть, поэтому мгновенная мощность изменяется с двойной частотой питающей сети.

Таким образом, в конденсаторе не происходит потребление энергии от источника, а происходит накапливание энергии в электрическом поле конденсатора в чётные четверти периода и возврат накопленной энергии источнику в нечётные четверти периода.

Напомним, что элемент, не потребляющий энергию от источника, называется реактивным и обладает реактивным сопротивлением. То есть конденсатор – это тоже реактивный элемент, обладающий реактивным сопротивлением

Диэлектрик, находящийся между обкладками конденсатора, всегда неидеален, то есть в нем всегда есть некоторые потери энергии, которые относительно малы и ими часто можно пренебречь. Если требуется учесть их в расчёте , то конденсатор заменяют схемой замещения (рис. 2-19), в которой параллельно ёмкости присоединено активное сопротивление R, потери энергии в котором имитируют потери энергии в реальном диэлектрике.

Рис. 2-19. Схема замещения реального конденсатора