Энергия электрического поля

Энергия заряженного конденсатора

В заряженном конденсаторе электрическое поле напряженностью $E$ создается зарядами на обоих обкладках. Таким образом, напряженность поля одной обкладки равна $E\over 2$. И в этом поле находится заряд $q$ другой пластины. Расстояние между обкладками $d$. Следовательно, потенциальная энергия такого конденсатора равна:

$$W={qEd\over 2}$$

Учитывая, что $Ed=U$, получим:

$$W={qU\over 2}$$

Таким образом, энергия заряженного конденсатора прямо пропорциональна сообщенному заряду и напряжению между обкладками. Для конкретного конденсатора эти две величины связаны через электроемкость:

$$С={q\over U}$$

Поскольку на практике электроемкость конденсатора чаще всего известна, в формуле энергии удобно заряд выразить через нее. Окончательно получим:

$$W={CU^2\over 2}$$

При выводе данной формулы предполагалось, что конденсатор плоский, и его электрическое поле однородно. Однако, формула справедлива для любого конденсатора любой формы.

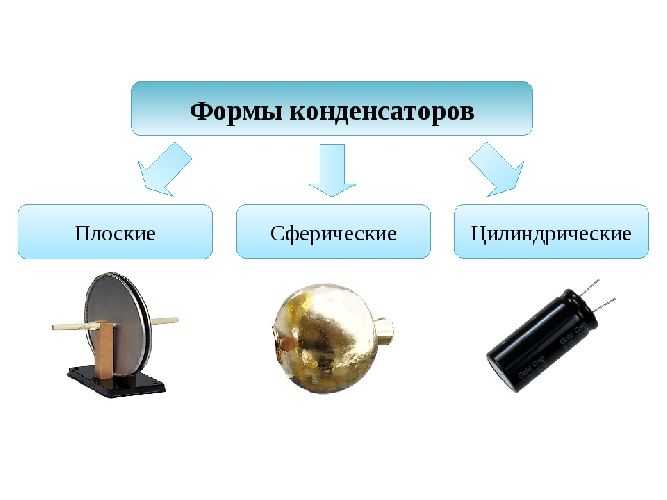Рис. 3. Плоский, сферический и цилиндрический конденсаторы.

Конденсатор, поле которого неоднородно, можно представить в виде бесконечного множества элементарных конденсаторов, соединенных параллельно, поле которых хотя и различно, но в пределах каждого элементарного конденсатора однородно. Емкость параллельных конденсаторов равна сумме составляющих емкостей. А поскольку при параллельном соединении напряжение на всех элементарных конденсаторах будет одно и то же, то в формуле энергии можно заменить значение электроемкости суммой элементарных емкостей. Формула останется справедливой.

Фактически, если поле конденсатора неоднородно, это повлияет лишь на распределение зарядов по обкладкам. Общая энергия при сохранении общей емкости и общего напряжения останется неизменной.

Что мы узнали?

Поскольку заряд в электрическом поле обладает некоторой потенциальной энергией, то заряженный конденсатор также обладает энергией. Энергия заряженного конденсатора зависит только от его емкости и от напряжения на нем. Форма конденсатора и распределение поля внутри него роли не играет.

1. /10

   Вопрос 1 из 10

   Как можно описать «движение вобще» без Системы Отсчета ?

   • необходимо брать точные формулы
   • необходимо делать более точные измерения
   • необходимо пользоваться лучшими инструментами
   • это невозможно

ЭКСПЕРИМЕНТ 1

Определение ёмкости конденсатора методом разрядки

1.Соберите на рабочей части экрана замкнутую электрическую цепь, показанную ниже на рис.2. Для этого сначала щёлкните мышью на кнопке э.д.с.,расположенной в правой части окна эксперимента. Переместите маркер мыши на рабочую часть экрана, где расположены точки, и щёлкните маркером мыши в виде вытянутого указательного пальца в том месте, где должен быть расположен источник тока. Подведите маркер мыши к движку появившегося регулятора э.д.с., нажмите на левую кнопку мыши, удерживая её в нажатом состоянии, меняйте величину э.д.с. и установите 10 В. Аналогичным образом включите в цепь 4 других источника тока. Суммарная величина э.д.с. батареи должна соответствовать значению, указанному в таблице 1 для вашего варианта.

Таким же образом разместите далее на рабочей части экрана 7 ламп Л1-Л7 ( кнопка ), Ключ К (кнопка ), вольтметр (кнопка ), амперметр (кнопка ), конденсатор (кнопка ). Все элементы электрической цепи соедините по схеме рис.1 с помощью монтажных проводов (кнопка ).

2. Щёлкните мышью на кнопке «Старт». Должна засветиться лампа Л7, а надпись на кнопке измениться на «Стоп». Курсором мыши замкните ключ К.

3. После установления в цепи стационарного тока ( должны погаснуть лампы Л5 и Л6 и светиться лампы Л1-Л4) запишите показания электроизмерительных приборов в таблицу 2.

4. Нажмите на кнопку «Стоп» и курсором мыши разомкните ключ К.

5. Двумя короткими щелчками мыши на кнопке «Старт» запустите и остановите процесс разрядки конденсатора. Показания амперметра будут соответствовать начальному току разрядки конденсатора I0. Запишите это значение в таблицу 3.

6. Вновь замкните ключ, зарядите конденсатор и повторите п.п. 5, 6 ещё 4 раза.

7. Для каждого опыта рассчитайте It= I0/2,7- силу тока, которая должна быть в цепи разрядки конденсатора через время релаксации t и запишите эти значения в таблицу 3.

8. При разомкнутом ключе нажатием кнопки «Старт» запустите процесс разрядки конденсатора и одновременно включите секундомер.

9. Внимательно наблюдайте за изменением показаний амперметра в процессе разрядки конденсатора. Остановите секундомер и синхронно нажмите кнопку «Стоп» при показании амперметра, равном или близким к It. Запишите это значение времени t1 в таблицу 3.

10. Проделайте опыты п.п.8, 9 ещё 4 раза.

Таблица 1. Суммарное значение э.д.с. источников тока

Вариант	1	2	3	4	5	6	7	8
Э.д.с.,В	50	49	48	47	46	45	44	43

Таблица 2. Определение сопротивления лампы.

№п/п

I, А

U, В

R, Ом

Номер опыта	1	2	3	4	5	Среднее значение
I0, А
It, А
t, с
C, Ф

Таблица 3. Результаты измерений и расчётов.

ОБРАБОТКА РЕЗУЛЬТАТОВ:

1. По закону Ома для участка цепи Л1-Л4: и результатам измерений, приведённым в таблице 2, определите сопротивление одной лампы.

2. По формуле (при разрядке конденсатора квазистационарный ток протекает по 6 последовательно соединённым лампам) определите ёмкость конденсатора и запишите эти значения в таблицу 3.

3. Рассчитайте погрешности измерений и сформулируйте выводы по результатам проделанной работы.

Точечный заряд и бесконечная плоскость.

Вычислим энергию, которой обладает точечный заряд вблизи
заземленной проводящей плоскости (см. ).
Сила, действующая на заряд известна. Вычислим работу, совершаемую этой силой, при перемещении
заряда в бесконечность. При бесконечном расстоянии энергия — 0.

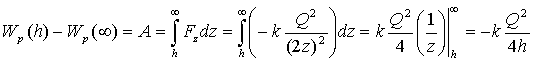    (16.48)

теперь найдем ту же самую величину как энергию взаимодействия
двух точечных зарядов: самого заряда и его зеркального отображения по формуле (16.2).

Результат получился в 2 раза больше?! Дело в том, что за плоскостью на самом деле поля нет,
поэтому от полученного выражения нужно оставить только половину, что как раз и совпадает с (16.48).

Мера энергии заряженного конденсатора

При расчёте фильтров цепей питания и прочих электрических фильтров встаёт задача определения номиналов. Кажется, достаточно взять формулу частоты резонансного контура, но простота обманчива. Легко убедиться, что одинаковому ответу соответствует множество значений. Которое выбрать?

Чем больше мощность источника, питания прибора, тем большая энергия здесь проходит в единицу времени. Для конденсатора она зависит от квадрата напряжения и ёмкости, для дросселя – от величины электрического тока и индуктивности. Узнав период единственного колебания, эту цифру легко привязать к мощности, как выполняемой работе в единицу времени.

В результате инженер сумеет сказать приблизительно, какого размера ёмкость требуется в конкретном случае. Расчёт ведётся изначально по энергии заряженного конденсатора.

Аналогичное происходит в любой цепи. Конденсаторы служат для фильтрации и гальванической развязки, обязаны легко пропускать нужную частоту и оставаться ёмкими, чтобы не стать бутылочным горлышком в системе.

Из истории

Первым конденсатором считается лейденская банка. Её разработали независимо сразу двое учёных:

1. Эвальд Георг фон Клейст (11 октября 1745 года).
2. Питер ван Мушенбрук (1745 – 1746 годы).

Двумя десятилетиями позже на свет появился электрофорус (1762 год), рассматриваемый как первый плоский конденсатор. Тогда не существовало терминов, вопросы накопления заряда мало интересовали. Учёные пока что развлекались получением статического заряда. К примеру, ван Мушенбрук испытывал лейденскую банку на слишком смелых студентах, когда сам оказался однажды полупарализован электрическим зарядом.

Наука не шла вперёд, хотя светила, включая Бенджамина Франклина, вовсю толкали паровоз. Современный этап развития физики начался с Алессандро Вольта. Учёный оказался привлечён конструкцией электрофоруса и заинтригован. Натёртая резина могла сколь угодно долго заряжать металлическую пластину. В то время предполагалось, что электричество переносится флюидами атмосферы, и Вольта считал аналогично. Узрев, что электрофорус способен запасать заряд, учёный решил посчитать и количество.

Конденсатор с частичным заполнением-2.

Пусть теперь диэлектрик заполняет конденсатор по-другому (рис.16.7). Сторона пластины равна а.
Очевидно, что такую систему можно рассмотреть как два параллельно соединенных конденсатора. Далее
все делаем по аналогии с п.10 и получаем следующее выражение для силы

    (16.59)

Опять видим, что сила направлена в сторону диэлектрика
с меньшей диэлектрической проницаемостью. Учтем, что при этом распределение
зарядов на пластинах конденсатора меняется. Однако напряженности поля справа и слева от границы равны.

Через характеристики поля сила, действующая на единицу поверхности, выражается следующим образом

    (16.60)

Формулы (16.57) и (16.60) очень похожи.

Можно сделать общий вывод:

Lex: Сила, действующая на границу диэлектрика, пропорциональна разности плотностей энергии электростатического поля и направлена в сторону диэлектрика с меньшей диэлектрической проницаемостью.

Теперь мы легко можем рассчитать, на какую высоту поднимется жидкий диэлектрик между двумя
заряженными пластинами ().
Остановит подъем гидростатическое давление. Сверху над диэлектриком — вакуум. Тогда

отсюда высота подъема

Попробуйте решить ту же задачу, если конденсатор подключен
к источнику питания. Результат должен быть аналогичен (16.60). Если ошибетесь
со знаком, то посмотрите разъяснения Фейнмана (т.5 стр 158 и 213).

Концепция Вольты

Как свидетельствуют записки учёного, уже в 1778 году он получил представление о разнице потенциалов, которые называл tension – напряжение. С 1775 года Вольта придерживается концепции электрической ёмкости – capacita, выдвинутой его учителем Беккарией. Вольта уже знает, что электрофорус способен накопить заряд, называет прибор конденсатором, и решает подтвердить теорию практикой. Иначе – найти взаимосвязь напряжения, ёмкости и объёмом (quantita) заряда.

Вольта начал с лейденской банки. Он заряжал её от статического генератора и пробовал определить энергию конденсатора тремя путями:

1. Наблюдал получаемую искру электрической дуги от различной конструкции лейденских банок, заряженных одинаковым напряжением.
2. Измерял количество произведённой электростатическими генераторами трения работу, пока показания электрометра не росли до определённого уровня.
3. Разряжал лейденские банки на открытом воздухе и пытался сравнить производимый ими электрический шок по истечении времени.

Все перечисленное привело исследователя к странным выводам, что высокие лейденские банки более вместительные (при одинаковых площадях обкладок и прочих равных условиях). Вероятно, это связано со скоростью разряда их дуги на воздухе вследствие различий в кривизне поверхностей. Силу разряда Вольта увязывал с электрическим током: чем быстрее течёт флюид, тем более жаркий (по ощущениям) эффект. В результате, Вольта счёл, что разница потенциалов единственная определяет процесс возникновения удара.  Он решил, что напряжение допустимо измерить двумя путями:

1. Через количество оборотов генератора статического заряда.
2. Сравнивая силу электрического удара при разряде лейденской банки.

Вольта нашёл, что заряжая пустую лейденскую банку от полной, шок получается вдвое слабее. Постепенно (1782 год) Вольта пришёл к выводу, что вышеуказанные величины соотносятся между собой: tension x capacity ~ load, в современном мире выглядит как U C = q или C = q / U.

Вольта заключил, что ёмкость больше там, где при меньшем напряжении вмещается больше заряда. Последовало заключение, что количество накопленного флюида прямо пропорционально площади обкладок плоского конденсатора. Что согласуется с современными формулами. Вольта обобщил знания на случай произвольного проводника (экспериментировал со стержнями лейденских банок). Изменяя расстояние между обкладками, установил:

С ~ S / d.

Что фактически стало выражением ёмкости плоского конденсатора. Вольта объяснил зависимость наличием некоего сопротивления (resistance) между обкладками, подразумевая воздух. Изменяя дистанцию, удаётся варьировать этот параметр в обе стороны. Это слегка не согласуется с современными концепциями, но Вольта помог Георгу Ому 40 лет спустя вывести зависимость между током и напряжением.

Фактически измерения проделывались на основе работы поля, проявлявшейся лишь вследствие заряда конденсатора. Очевидно, что указанная величина равна энергии – одной из первых физических характеристики, использованных для вывода аналитических выражений.

Плоский конденсатор.

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:

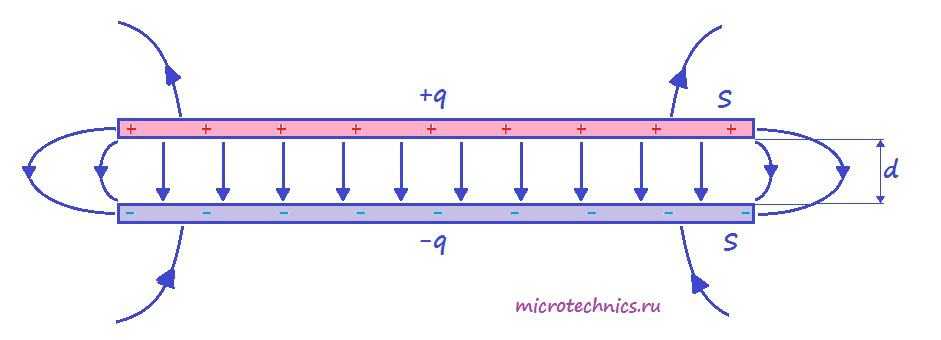
Такое устройство называется плоским конденсатором, а пластины — обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.

Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:

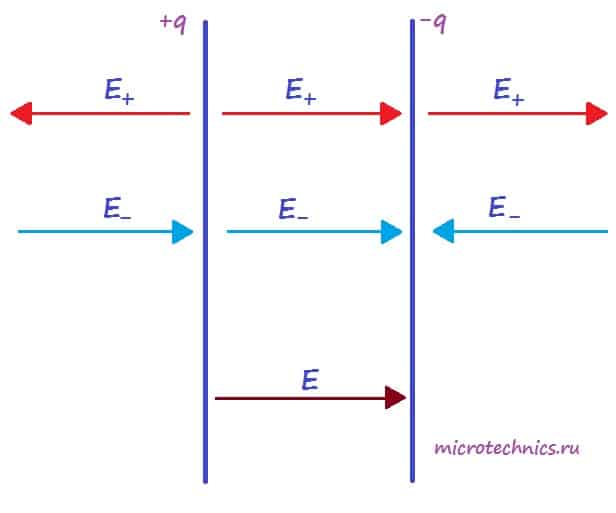
Каждая из обкладок конденсатора в отдельности создает электрическое поле:

• положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
• отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}

Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:

E = frac{sigma}{2varepsilon_0thinspacevarepsilon}

Здесь sigma— это поверхностная плотность заряда: sigma = frac{q}{S}, а varepsilon — диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:

E_+ = E_- = frac{q}{2varepsilon_0thinspacevarepsilon S}

Но направления векторов разные — внутри конденсатора вектора направлены в одну сторону, а вне — в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:

E = E_+ + E_- = frac{q}{2varepsilon_0thinspacevarepsilon S} + frac{q}{2varepsilon_0thinspacevarepsilon S} = frac{q}{varepsilon_0thinspacevarepsilon S}

А какая же будет величина напряженности вне конденсатора? А все просто — слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0

Энергия системы точечных зарядов.

Пусть имеются два неподвижных точечных заряда (рис.16.1). Поле — электростатическое
и потенциальное, силы консервативны. Работа, которую совершает поле заряда q₁
при переносе заряда q₂ из бесконечности в точку 2 в соответствии с (6.3) и (6.16) равна

Считая, что
W_p¥(r_1¥¥)=0,
получаем

    (16.2)

Это энергия взаимодействия двух точечных зарядов, которая
в зависимости от знака зарядов, может быть как положительной, так и отрицательной.
Можно говорить, что заряд q₂ в поле, созданном зарядом q₁
обладает потенциальной энергией W_p. Из симметрии формулы ясно, что можно рассуждать и наоборот.

Теперь добавим в систему третий заряд q₃ (рис.16.2). По аналогии

а энергия всей системы зарядов

Заметим, что в это выражение все величины входят симметрично,
т.е. безразлично, в какой последовательности мы собирали систему. Эта энергия
не зависит от процесса, а лишь от состояния системы. Потенциальная энергия —
это функция состояния системы. Нулевое значение берется при бесконечном удалении
зарядов друг от друга. Заметим также, что это энергия всей системы, энергия
взаимодействия, поэтому бессмысленно говорить, что какая-то часть этой энергии
принадлежит одному из зарядов. Здесь мы не учитываем собственную энергию каждого точечного заряда.

Это та энергия, которую нужно затратить, чтобы собрать
из бесконечно малых порций заряда точечный заряд. Формально она бесконечна,
так как необходимо уложить заряды в нулевой объем. Кроме того, эту энергию изменить
весьма проблематично. Поэтому можно считать, что это постоянная величина. А
мы помним, что потенциальную энергию определяют с точностью до постоянной, которую
всегда можно отбросить, так как смысл имеет не сама энергия, а ее изменение.

Обобщив сказанное, можно записать потенциальную энергию взаимодействия системы из N точечных зарядов

    (16.5)

Множитель 1/2 появляется в связи с тем, что при суммировании каждая пара зарядов входит в формулу два раза.
Перепишем это выражение несколько по иному

, N>1    (16.6)

где j_i — потенциал в точке, где находится заряд q_i,
созданный всеми другими зарядами.

Напомним, что энергия одного точечного заряда в поле, созданном всеми другими
зарядами (рис.16.2) вычисляется в соответствии с формулами (6.16)-(6.18) как

    (16.7)

§ 19. Напряжённость электростатического поля. Принцип суперпозиции

Для изучения свойств электростатического поля удобно использовать такую его характеристику, которая не зависит от числового значения пробного заряда и позволяет определить силу, действующую на заряд со стороны поля в любой его точке. Для гравитационного поля такой характеристикой, не зависящей от массы тела, является ускорение свободного падения . Какая физическая величина является характеристикой электростатического поля?

Напряжённость электростатического поля. Пусть электростатическое поле создано в вакууме точечным зарядом Q > 0. Если в некоторую точку поля поместить пробный положительный заряд q, на него будет действовать кулоновская сила отталкивания, модуль которой .

Сила не может служить характеристикой поля, так как её модуль пропорционален значению пробного заряда q. Однако отношение модуля силы, которой электростатическое поле точечного заряда Q действует на пробный заряд q, не зависит от значения пробного заряда:

(19.1)

и, следовательно, может служить характеристикой поля.

Эту характеристику называют напряжённостью электростатического поля и обозначают . Напряжённость характеризует силовое действие поля на вносимые в него заряды.

Напряжённость электростатического поля — физическая векторная величина, равная отношению силы, которой поле действует на пробный заряд, к значению этого заряда:

(19.2)

С учётом выражений (19.1) и (19.2) можно определить модуль напряжённости электростатического поля, созданного точечным зарядом Q, в точке, находящейся на расстоянии r от него:

Таким образом, модуль напряжённости поля, создаваемого в вакууме точечным зарядом, прямо пропорционален модулю этого заряда и обратно пропорционален квадрату расстояния между зарядом и точкой, в которой определяют значение напряжённости.

Если заряд Q находится в однородной среде с диэлектрической проницаемостью ε, то модуль напряжённости поля .

Из выражения  следует, что единицей напряжённости электростатического поля в СИ является ньютон на кулон . В СИ широко используют другое название этой единицы — вольт на метр .

Зная напряжённость электростатического поля, можно определить силу, действующую на любой точечный заряд в любой точке этого поля:

(19.3)

Рис. 104

Напряжённость поля, как и сила, величина векторная. Направление напряжённости поля совпадает с направлением силы, действующей на положительный пробный электрический заряд. Напряжённость в любой точке электростатического поля точечного заряда направлена вдоль прямой, соединяющей эту точку и точечный заряд, создающий поле. Напряжённость поля, созданного точечным положительным зарядом Q > 0, направлена от заряда, а напряжённость поля, созданного точечным отрицательным зарядом Q < 0, — к заряду (рис. 104).

От теории к практике

Рис. 105

1. Как изменится модуль напряжённости в некоторой точке поля, созданного точечным зарядом Q, если: а) расстояние r от заряда до этой точки увеличить вдвое; б) заряд Q увеличить вдвое, а расстояние r от заряда до этой точки уменьшить вдвое?

2. Как направлена в точке А напряжённость поля, созданного неподвижным точечным зарядом (рис. 105)? Чему равен модуль напряжённости поля в этой точке?

Рис. 105.1

Модуль напряжённости поля уединённой проводящей сферы радиусом R, заряд которой Q (рис. 105.1), в точках на её поверхности r = R и вне сферы на расстоянии r > R от её центра определяют по формуле . В точках, находящихся внутри проводящей сферы r < R, напряжённость равна нулю , если внутри этой сферы нет электрических зарядов.

Напряжённость электростатического поля, создаваемого равномерно заряженной бесконечной плоскостью, одинакова во всех точках полупространства с каждой стороны от плоскости (при этом ), а её модуль

где S — площадь некоторого участка плоскости, — модуль заряда этого участка (рис. 105.2).

Рис. 105.2

Интересно знать

Кроме гравитационного поля у Земли есть электрическое и магнитное поля. Модуль напряжённости электрического поля у поверхности Земли в среднем составляет . Электрическое поле Земли меняется во времени. Избыточный отрицательный электрический заряд земного шара колеблется около –6 · 105 Кл.

Поле заряженного конденсатора

Рассмотрим плоский конденсатор, состоящий из двух пластин. При заряде на этих пластинах (обкладках) накапливаются заряды разных знаков. Число носителей заряда на обкладках конденсатора одинаково, и они свободно распределяются по обкладкам. Следовательно, распределение заряда на обкладках будет равномерным и равным. Силовые линии электрического поля выходят из положительных зарядов, и приходят в отрицательные. Значит, их распределение будет равномерным. Таким образом, поле заряженного конденсатора можно считать однородным:

Рис. 1. Электрическое поле внутри плоского конденсатора.

Калькулятор расчета запасаемой энергии в конденсаторе

Конструктивно конденсатор представляет собой емкостной элемент, состоящий из двух параллельно расположенных пластин, пространство между которыми заполнено диэлектриком.

Устройство конденсатора

Принцип работы конденсатора заключается в способности накапливать определенную величину заряда на пластинах и отдавать их обратно в сеть при прохождении через него переменного тока. Для цепи постоянного тока конденсатор представляет собой разрыв, но пластины все равно способны накапливать заряд. Основным параметром конденсатора является емкость, выражающаяся в Фарадах и способность накапливать заряд, выражаемая величиной энергии в Джоулях.

Если емкость конденсатора указывается на корпусе элемента и является его паспортным значением, то количество запасаемой энергии можно определить путем вычислений. Наиболее простым способом вычисления является использования онлайн калькулятора.

Для этого выполните такую последовательность действий:

• Внесите в первую графу калькулятора значение напряжения на конденсаторе в Вольтах;
• Укажите во втором поле величину емкости элемента в микрофарадах;
• Внесите значения сопротивления конденсатора и нажмите кнопку «Рассчитать».

В результате онлайн калькулятор расчета запасаемой энергии в конденсаторе выдаст значение заряда и времени, расходуемого на полный заряд емкостного элемента, подключенного к цепи.

Расчет величины заряда, накапливаемого в конденсаторе, и времени, необходимого для накопления этого заряда производится по таким формулам:

• W – это количество запасаемой энергии в конденсаторе;
• U – величина напряжения, приложенного к конденсатору;
• C – емкость конденсатора.

Для определения времени, затрачиваемого на накопление этого количества запасаемой энергии, в калькуляторе используется формула: Tзар = R*C

• Tзар — период времени, необходимый для накопления заряда, зависящий от параметров элемента;
• R – величина омического сопротивления конденсатора;
• C – емкость конденсатора.

Источник