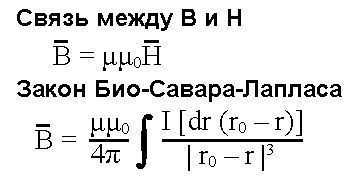Индукция магнитного поля

Появление понятия магнитной индукции

На заре эпохи развития электричества люди стали исследовать сопутствующие явления. Так, Ханс Эрстед в 1819 году обнаружил: проводник с током создает вокруг круговое магнитное поле, Андре-Мари Ампер показал, что если направление движения зарядов совпадает, соседствующие проводники притягивают друг друга. Конец спорам положило создание закона Био-Савара (отечественные источники добавляют Лапласа), описывающего величину, направление магнитной индукции в точке пространства. Источники допускают оговорку касательно того, что исследования велись постоянного тока.

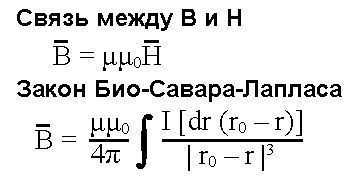
Взаимосвязь индукции и напряженности магнитного поля

Интегрирование (см. рисунок) идет по контуру с током. В формуле r подразумевает элементарную среднюю точку текущего отрезка, r0 – место пространства, для которого вычисляется магнитная индукция

Обратите внимание, в знаменателе дроби за интегралом перемножаются два вектора. Результатом выходит величина, направление которой определим по правилу буравчика (левой или правой руки)

Интегрирование ведется по элементу контура dr, r – средняя точка малого отреза полной длины. Идентичные разности в числителе и знаменателе сократим, остается вверху единичный вектор, задающий направление результата.

Формула показывает, как найти поле для контуров любой формы, проводя интегрирование по точкам. Современные численные методы лежат в основе действия компьютерных приложений (наподобие Maxwell 3D) по решению соответствующей задачи. Уравнение согласуется с законами Гаусса (магнитной индукции) и Ампера (циркуляции магнитного поля). Георг Ом использовал знания о компасе, выводя известную зависимость. Форму линий поля получим при помощи магнитных стрелок и силы оставления направления неизменным (см. заметку про закон Ома для участка цепи). Это будет картина магнитной индукции в пространстве, экспериментально подтвердившая закон Био-Савара-Лапласа.

Позволило сделанное Амперу в 1825 году показать: электрический ток в некоторых случаях является аналогом постоянного магнита. Появилась новая модель, которая лучше согласовывалась с действительностью, нежели схема диполей Пуассона. Подобная абстракция объясняла отсутствие в природе изолированных магнитных полюсов. По современным представлениям, кусок стали намагничивается, оттого что диполи элементарных частиц и молекул приобретают упорядоченность. На этом основаны контуры размагничивания сердечников трансформаторов, которые перед выключением питания вызывают затухающие колебания тока. В результате эффект упорядоченности размывается, выраженные свойства пропадают.

Спин электрона

Наличие магнитного момента объясняется существованием спинов (понятие введено в 20-х годах XX века) – угловой момент частиц микромира. Реальные, не абстрактные вещи, существование подтверждено экспериментально (Штерн-Герлах). Спин является векторной величиной, одинаковой для всех частиц одного типа (например, электронов), описывается специальным квантовым числом. В СИ единицей измерений служит Дж с, как и для другого углового момента (постоянной Планка). Иногда применяется упрощенная безразмерная запись. Постоянная Планка опускается. Указывается просто спиновое квантовое число (s, ms).

Благодаря наличию спина, элементарная частица обзаводится магнитным моментом, вычисляемым по формуле: в числителе произведение спинового углового момента на заряд частицы и g-фактор (постоянные, приводимые в различных справочниках для тех или иных элементарных частиц); в знаменателе – удвоенная масса элементарной частицы. Как видите, поддается учету, максимальную намагниченность материала в заданных условиях можно заранее рассчитать. Настоящим триумфом квантовой электродинамики явилось предсказание g-факторов для некоторых элементарных частиц.

Открытие Майклом Фарадеем в 1831 году генерации переменным магнитным полем кругового электрического показало: два явления тесно связаны, что явилось предпосылкой созданию (четырех) уравнений Максвелла, частным случаем которых являются большинство формул в этой области, считая упомянутые выше. Исследования шли своим чередом, но несколько разными путями. Интеграцию произвел лорд Кельвин, известный как Вильям Томпсон, который показал наличие H (напряженность) и B магнитной индукции, первая характеризует модель Пуассона, вторая – Ампера.

Физический смысл магнитной индукции (МИ)

Возможность действовать на предмет магнитным полем (МП) определяет сущность настоящей индукции. Она появляется в момент перемещения в катушке индуктивности магнита постоянной природы. Результатом такого движения является появление тока, с одновременным увеличением магнитного потока. Поскольку обмотка у катушки металлическая, а структура металла – кристаллическая решётка, то можно объяснить физические свойства этого явления.

Электроны, находящиеся в этой решётке, при отсутствии магнитного воздействия находятся в покое. Движения никакого нет. Оно начинается в тот момент, когда электроны попадают под воздействие переменного МП (поле изменяется при перемещении постоянного магнита).

Значение возникающего в катушке тока зависит от диаметра жилы и количества витков, физических характеристик магнита и скорости его движения.

Единица размерности в системе Си рассматриваемой характеристики – тесла. Она обозначается буквами Тл.

Важно! Электроны в решётке, после попадания катушки в МП, разворачиваются под некоторым углом и выстраиваются вдоль силовых линий МП. Количество ориентированных частиц и однородность их размещения зависимы от величины поля

Вектор – это вектор индукции магнитного поля (градиентный параметр МП).

Причины возникновения индукционного тока в движущихся и неподвижных проводниках

Причин, по которым может происходить изменение магнитного потока, пронизывающего замкнутый контур, две:

1. Изменение магнитного потока вследствие перемещения всего контура или отдельных его частей в магнитном поле, которое не изменяется со временем;
2. Изменение магнитного поля при неподвижном контуре.

Перейдем к рассмотрению этих случаев подробнее.

Перемещение контура или его частей в неизменном магнитном поле

При движении проводников и свободных носителей заряда в магнитном поле возникает ЭДС индукции. Объяснить возникновение δинд можно действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца здесь – это сторонняя сила.

Пример 2

На рисунке мы изобразили пример индукции, когда прямоугольный контур помещен в однородное магнитное поле B→ направленное перпендикулярно плоскости контура. Одна из сторон контура перемещается по двум другим сторонам с некоторой скоростью.

Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Отражена составляющая силы Лоренца, которая действует на свободный электрон

На свободные заряды подвижной части контура воздействует сила Лоренца. Основная составляющая силы Лоренца в данном случае направлена вдоль проводника и связана с переносной скоростью зарядов υ→. Модуль этой сторонней силы равен:

FЛ=eυ→B.

Работа силы FЛ на пути l равна:

A=FЛ·l=eυBl.

По определению ЭДС:

δинд=Ae=υBl.

Значение сторонней силы для неподвижных частей контура равно нулю. Для соотношения δинд можно записать другой вариант формулы. Площадь контура с течением времени изменяется на ΔS=lυΔt. Соответственно, магнитный поток тоже будет с течением времени изменяться: ΔΦ=BlυΔt.

Следовательно,

δинд=∆Φ∆t.

Знаки в формуле, которая связывает δинд и ∆Φ∆t, можно установить в зависимости от того, какие направления нормали и направления контура будут выбраны. В случае выбора согласованных между собой по правилу правого буравчика направлений нормали n→ и положительного направления обхода контура l→ можно прийти к формуле Фарадея.

При условии, что сопротивление всей цепи – это R, то по ней будет протекать индукционный ток, который равен Iинд=δиндR. За время Δt на сопротивлении R выделится джоулево тепло:

∆Q=RIинд2∆t=υ2B2l2R∆t

Парадокса здесь нет. Мы просто не учли воздействие на систему еще одной силы. Объяснение заключается в том, что при протекании индукционного тока по проводнику, расположенному в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, которая связана с относительной скоростью движения зарядов вдоль проводника. Благодаря этой составляющей появляется сила Ампера FА→.

Для рассмотренного выше примера модуль силы Ампера равен FA =IBl. Направление силы Ампера таково, что она совершает отрицательную механическую работу Aмех. Вычислить эту механическую работу за определенный период времени можно по формуле:

Aмех=-Fυ∆t=-IBlυ∆t=-υ2B2l2R∆t

Проводник, перемещающийся в магнитном поле, испытывает магнитное торможение. Это приводит к тому, что полная работа силы Лоренца равна нулю. Джоулево тепло может выделяться либо за счет уменьшения кинетической энергии движущегося проводника, либо за счет энергии, которая поддерживает скорость перемещения проводника в пространстве.

Изменение магнитного поля при неподвижном контуре

Определение

Вихревое электрическое поле – это электрическое поле, которое вызывается изменяющимся магнитным полем.

В отличие от потенциального электрического поля работа вихревого электрического поля при перемещении единичного положительного заряда по замкнутому проводящему контуру равна δинд в неподвижном проводнике.

В неподвижном проводнике электроны могут приводиться в движение только под действием электрического поля. А возникновение δинд нельзя объяснить действием силы Лоренца.

Первым, кто ввел понятие вихревого электрического поля, был английский физик Джон Максвелл. Случилось это в 1861 году.

Фактически, явления индукции в подвижных и неподвижных проводниках протекают одинаково. Так что в этом случае мы тоже можем использовать формулу Фарадея. Отличия касаются физической причины возникновения индукционного тока: в движущихся проводниках δинд обусловлена силой Лоренца, в неподвижных – действием на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

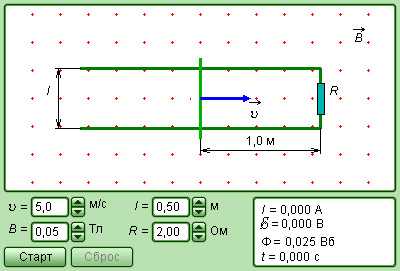
Рисунок. Модель электромагнитной индукции

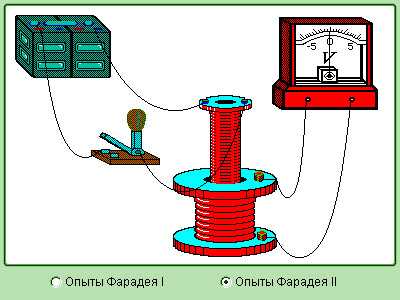
Рисунок. Модель опытов Фарадея

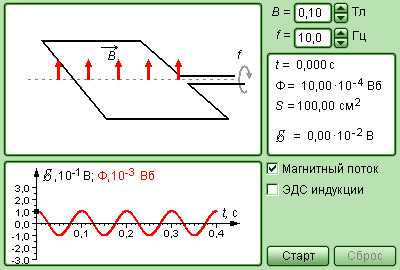
Рисунок . Модель генератора переменного тока

Как вам статья?

Мне нравится1Не нравится

Павел Бакалавр «210400 Радиотехника» – ТУСУР. Томский государственный университет систем управления и радиоэлектроники
Написать Пишите свои рекомендации и задавайте вопросы

Основные формулы и методические рекомендации по решению задач на электромагнитную индукцию

«Превратить магнетизм в электричество…»

Майкл Фарадей

Данная тема будет посвящена рассмотрению основных формул и методических рекомендаций по решению задач на электромагнитную индукцию

Рассмотрим основные понятия электромагнитной индукции. Магнитныйпоток – это скалярная физическая величина, численно равная произведению модуля вектора магнитной индукции на площадь поверхности, ограниченной контуром, и на косинус угла между нормалью к поверхности и направлением линий магнитной индукцией.

Изменение магнитного потока влечет за собой такое явление, как электромагнитнаяиндукция . Чем быстрее изменяется магнитный поток, тем большая сила тока возникает в замкнутом контуре.

В результате явления электромагнитной индукции, в контуре возникает электродвижущая сила – она так и называется ЭДСиндукции .

Поскольку сила тока связана с индукцией порождаемого им магнитного поля, а магнитная индукция, в свою очередь, связана с магнитным потоком, возникает явление самоиндукции. Самоиндукция

– это явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока. То есть, при изменении силы тока, в цепи возникает индукционный ток, который стремится препятствовать этому изменению. В связи с этим, вводится такая величина, какиндуктивность – коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур. Иными словами, индуктивность характеризует способность проводника влиять на быстроту установления тока в цепи. Она, конечно, обнаруживает себя только при изменении силы тока в цепи.

Сведём в таблицу основные формулы по рассматриваемой теме.

Формула	Описание формулы
Магнитный поток через контур площадью S , гдеB – модуль вектора магнитной индукции,a – угол между направлением вектора магнитной индукции и нормалью к плоскости контура.
ЭДС индукции, возникающая в контуре при изменении магнитного потока на величину DF за промежуток времени Dt
ЭДС индукции, возникающая в движущемся со скоростью проводнике длиной , где a – угол между направлением вектора магнитной индукции и направлением вектора скорости.
Коэффициент самоиндукции (индуктивность) контура.
ЭДС самоиндукции, возникающая в контуре при изменении силы тока на величину DI за промежуток времени Dt .
Индуктивность соленоида объёмом V , гдеm – магнитная проницаемость среды,m 0 – магнитная постоянная Гн/м,n – число витков на единицу длины.
Энергия магнитного поля катушки с индуктивностью L , гдеI – сила тока, F – магнитный поток.
Энергия магнитного поля соленоида объёмом V , гдеB — модуль вектора магнитной индукции.

Методические рекомендации по решению задач на электромагнитную индукцию

1. Установить причину изменения магнитного потока через контур. Исходя из формулы, причиной может стать либо изменение магнитной индукции поля, либо изменение площади контура, а также угла между направлением линий магнитной индукции и нормалью к плоскости контура (чаще всего, это поворот рамки с током).

2. Записать закон электромагнитной индукции (закон Фарадея).

3. Если речь идет о поступательном движении проводника, применить формулу, по которой вычисляется ЭДС индукции в движущемся проводнике.

4. Определить изменение магнитного потока, рассматривая его в выбранные моменты времени t

1 иt 2 (как правило, это должны быть те моменты времени, которые описываются в задаче).

5. Подставить найденное выражение для изменения магнитного потока в закон Фарадея. При необходимости, используя дополнительные уравнения, составить систему и решить её относительно искомых величин.

Магнитная индукция

Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.

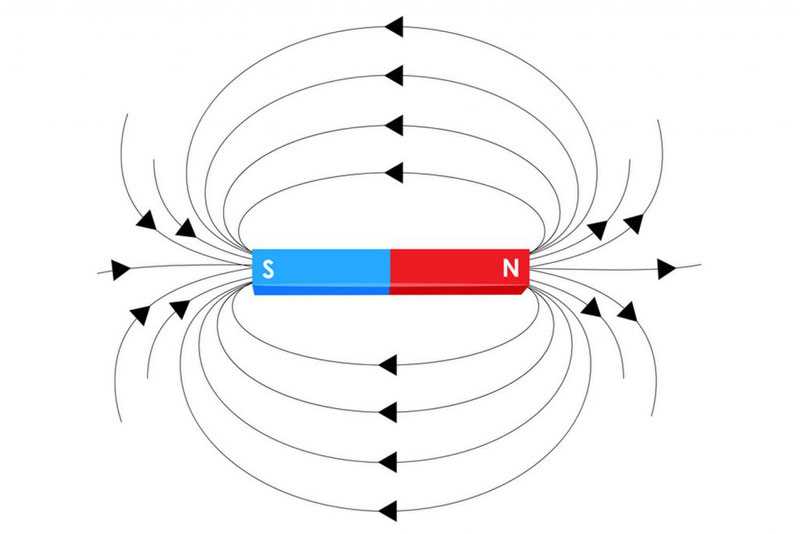Изображение магнитного поля при помощи силовых линий

Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.

Она обозначается буквой B и измеряется вТесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.

Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.

Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.

Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!

Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.

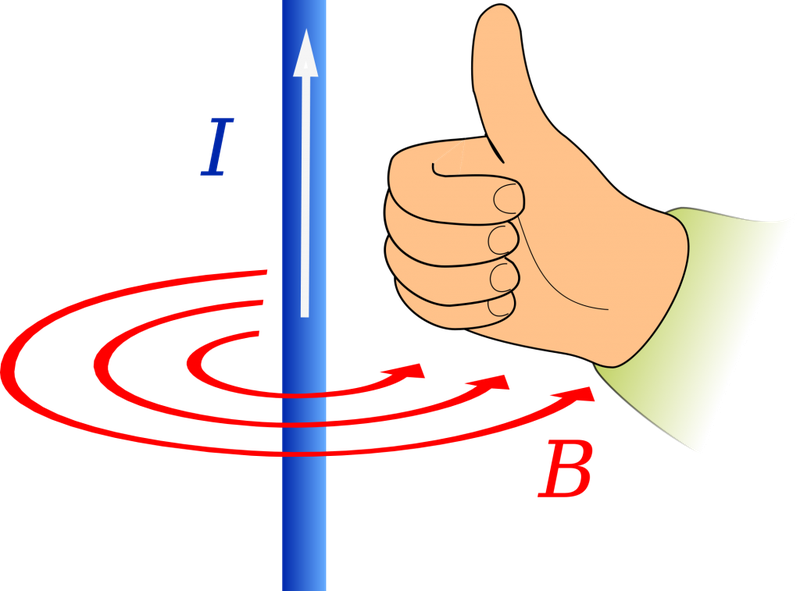
Формула индукции магнитного поля

ОПРЕДЕЛЕНИЕ

Векторной характеристикой магнитного поля является вектор магнитной индукции. Его обозначают как:

Направлением вектора магнитной индукции считают направление на север магнитной стрелки, которая может свободно вращаться в магнитном поле. Такое же направление имеет положительная нормаль к замкнутому контуру, по которому течет ток. Положительная нормаль имеет направление, совпадающее с направлением перемещения правого винта (буравчика), если его вращают по направлению тока в контуре.

Модуль вектора магнитной индукции можно установить, используя силу, которая действует на проводники с током, помещенные в магнитное поле (силу Ампера). Тогда модуль вектора равен частному от деления максимальной силы (), с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника ():

Рассматривая силу Лоренца, которая действует на заряженную частицу, движущуюся в магнитном поле, получают формулу для магнитной индукции в виде:

где – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; – это угол между векторами и . Направления , векторов и связаны между собой правилом левой руки.

Формулой, которая определяет величину вектора магнитной индукции в данной точке магнитного поля, считают так же следующее выражение:

где – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом , равным единице, если нормаль к рамке перпендикулярна направлению поля. Вращающий момент (M), действующий на контур с током I в однородном магнитном поле можно вычислить как:

где S – площадь, которую обтекает ток I. Следует помнить, что максимальный вращающий момент получается тогда, когда плоскость контура параллельна линиям магнитной индукции поля ().

Изменения в магнитосфере Земли

Характеристики земного МП меняются, в основном, вследствие того, что оно смещается относительно земного шара. Люди привыкли, что северный конец стрелы должен устремляться к северу. При обратной намагниченности диполя планеты ситуация будет противоположной. В обсерваториях фиксируются данные о состоянии МП планеты, и на их основе создаются геомагнитные карты. Они демонстрируют наличие отклонений в напряженности МП и положении силовых линий в некоторых уголках Земли. Эти явления называют магнитными аномалиями. Иногда их используют как индикаторы местоположения определенных ископаемых ресурсов.

Связь между индукцией и степенью напряженности поля широко используется в расчетах. Она позволяет вывести выражения для нахождения значения индукции в проводниках разных форм, сделанных из материалов с различными показателями магнитной проницаемости.

ЭДС индукции

\(~E_i = -\frac {\Delta \Phi}{\Delta t},\)

где E_i – ЭДС индукции, возникающая в контуре при равномерном изменении магнитного потока (В); ΔΦ = Φ₂ — Φ₁ – изменение магнитного потока от Φ₁ до Φ₂ (Вб); Δt – время изменения магнитного потока (с); ΔΦ/Δt – скорость изменения магнитного потока (Вб/с или В).

• Эту формулу можно применять только при равномерном изменении магнитного потока.
• При увеличении магнитного потока (ΔΦ > 0), ЭДС отрицательная (ℰ_i < 0), т.е. индукционный ток имеет такое направление, что вектор магнитной индукции индукционного магнитного поля направлен против вектора магнитной индукции внешнего (изменяющегося) магнитного поля (рис. 2 а).
• При уменьшении магнитного потока (ΔΦ < 0), ЭДС положительная (E_i > 0), т.е. индукционный ток имеет такое направление, что вектор магнитной индукции индукционного магнитного поля направлен в одну и ту же сторону с вектором магнитной индукции внешнего (изменяющегося) магнитного поля (рис. 2 б).
• Знак «–» в формуле будем учитывать в задачах, где указано как изменяется (увеличивается или уменьшается) магнитный поток.

Рис. 2

Так как магнитный поток равен \(~\Phi = B \cdot S \cdot \cos \alpha\) , то он может изменяться:

• или только за счет изменения магнитной индукции поля, тогда

  
  \(~\Delta \Phi = (B_2 — B_1) \cdot S \cdot \cos \alpha\) ;
  

• или только за счет изменения площади контура, тогда

  
  \(~\Delta \Phi = B \cdot (S_2 — S_1) \cdot \cos \alpha\) ;
  

• или только за счет поворота контура в магнитном поле, тогда

  
  \(~\Delta \Phi = B \cdot S \cdot (\cos \alpha_2 — \cos \alpha_1)\) ;
  

• или одновременно за счет изменения нескольких параметров, тогда

  
  \(~\Delta \Phi = B_2 \cdot S_2 \cdot \cos \alpha_2 — B_1 \cdot S_1 \cdot \cos \alpha_1\) .
  

При любом способе изменения магнитного потока в контуре возникает ЭДС индукции.

Индукционный ток

\(~I_i = -\frac {E_i}{R},\)

где I_i – индукционный ток в контуре (А), E_i – ЭДС индукции (В), R – сопротивление контура (Ом).

План определения направления индукционного тока:

1. Установите направление вектора магнитной индукции внешнего поля (\(~\vec B\)).
2. Выясните, как изменяется (увеличивается или уменьшается) поток магнитной индукции этого поля через поверхность контура.
3. Используя правило Ленца, установите направление вектора магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) :
   • если поток магнитной индукции через контур увеличивается, то вектор магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) направлен в противоположную сторону вектора магнитной индукции внешнего поля (\(~\vec B\)) ;
   • если поток магнитной индукции через контур уменьшается, то вектор магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) направлен в ту же сторону, что и вектор магнитной индукции внешнего поля (\(~\vec B\)) .
4. Используя правило правой руки, по направлению вектора магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) найдите направление индукционного тока.

ЭДС индукции движущегося проводника

Индукционный ток в проводниках, движущихся в магнитном поле, возникает за счет действия на свободные заряды проводника силы Лоренца. Поэтому направление индукционного тока в проводнике будет совпадать с направлением составляющей силы Лоренца на этот проводник.

С учетом этого можно сформулировать следующее правило левой руки для определения направления индукционного тока в движущемся проводнике: нужно расположить левую руку так, чтобы вектор магнитной индукции входил в ладонь, четыре пальца совпадали с направлением движения проводника, тогда отставленный на 90° большой палец укажет направление индукционного тока (рис. 3).

Рис. 3

• Если проводник движется вдоль вектора магнитной индукции, то индукционного тока не будет (сила Лоренца равна нулю).
• Ток не может идти поперек проводника (заряды под действием силы Лоренца смещаются к стенкам проводника и создавать ток не будут) (рис. 4).

Рис. 4

\(~E_i = B \cdot \upsilon \cdot l \cdot \cos \alpha ,\)

где E_i – ЭДС индукции движущегося проводника (В); υ – скорость движения проводника (м/с); В – модуль вектора магнитной индукции (Тл); l – длина проводника (м); α – угол между направлением движения проводника и вектором магнитной индукции.

Определение знака ЭДС индукции

На рисунке изображен замкнутый контур. Будем считать положительным направление обхода контура против часовой стрелки. Нормаль → n к контуру образует правый винт с направлением обхода.

Пусть магнитная индукция → B внешнего магнитного поля направлена вдоль нормали к контуру и возрастает со временем. Тогда Φ > 0 и Δ Φ Δ t . . > 0 . Согласно правилу Ленца индукционный ток создает магнитный поток Φ ‘ 0 . Линии магнитной индукции B’ магнитного поля индукционного тока изображены черным цветом. Следовательно, индукционный ток I_i согласно правилу буравчика направлен по часовой стрелке (против направления положительного обхода) и ЭДС индукции отрицательна. Поэтому в законе электромагнитной индукции должен стоять знак «–», указывающий на то, что ε i и Δ Φ Δ t . . имеют разные знаки:

Пример №1. Магнитный поток через контур проводника сопротивлением 3∙10 –2 Ом за 2 с изменился на 1,2∙10 –2 Вб. Найдите силу тока в проводнике, если изменение потока происходило равномерно.

ε i = ∣ ∣ ∣ Δ Φ Δ t . . ∣ ∣ ∣

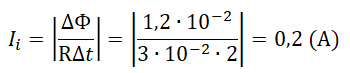
Как определяется направление вектора индукции магнитного поля?

За направление вектора индукции магнитного поля \  используют направление, в котором устанавливается под воздействием поля  утвердительного нормали к току с контору. Другими словами объясняют так: вектор идет в направление поступательного перемещения правого винта при вращении по направлению передвижения тока внутри контура.

Вектор индукции \ обладает направлением, которое начинается со стрелки южного полюса \ (она свободна передвигается в поле) к полюсу северному \.

Магнитное поле возникает из-за электрических зарядов (элементарными токами), движущиеся в нем.

Для того чтобы определить направление вектора магнитной индукции в проводнике с элементарным током, используют правило правой руки (Буравчика). Они формулируются так:

Для катушки с током: 4 согнутых пальца руки, которые обхватывают катушку, направляют по течению току. В это время оставленный большой палец на \ указывает на направление магнитной индукции \ в середине катушки.

Для прямого проводника с элементарным током: большой палец руки, который оставляется на \, направить по течению элементарного тока. В это время 4 согнутых пальца, которые держат проводник, показывают сторону, куда направлена индукция магнитного поля.

Задания по теме

Разберем примеры, в которых будет задействована данная формула и свойства.

Пример 1

Условие задачи:

Проводник представлен в квадратной форме. Каждая из сторон равна d. В данный момент по нему проходит элементарный ток силы I. Найдите индукцию магнитного поля в месте, где диагонали квадрата пересекаются.

Решение задачи следующее:

Сделаем рисунок, в котором плоскость совпадает с плоскостью проводника. Изобразим направление вектора индукции магнитного поля.

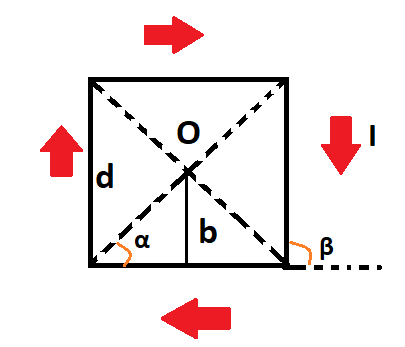
В данной точке О получаются проводники с элементарным током, которые расположены прямолинейно и вектор магнитной индукции поля перпендикулярен плоскости. Направления напряжености полей определяется в соответствием с правилом правого винта,то есть перпендикулярны плоскости изображения. Поэтому сумму векторов по принципу суперпозиции надо заменить на алгебраический вид. Получим следующее выражение: B=B₁+B₂+B₃+B₄ 

Из симметричности рисунка можно увидеть, что модули вектора индукции магнитного поля одинаковы. Получаем следующее: B=4B₁

В разделе физике «Электромагнетизм» использовали одну из формул, чтобы рассчитать модуль индукции прямолинейного проводника с элементарным током.

Чтобы формула подошла к данной задачи, ее применяют в следующем виде:

\

углы α и β, которые отмечены на рисунке:

\

Используем формулу \ и преобразуем с применением тригонометрического свойства:

\

Поскольку у нас квадратная форма, то следует заметить следующее:

\

Возьмем выведенные формулы и получим конечное выражение, то есть:

\

Ответ: \

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Пример 2

Условие задачи:

Бесконечно проводник с элементарным током (I) согнут под 90 градусов, который изображен на рисунке. Найдите вектор магнитной индукции однородного поля в точке А.

Решение задачи:

В точке А получается из двух частей проводника, то есть:

\

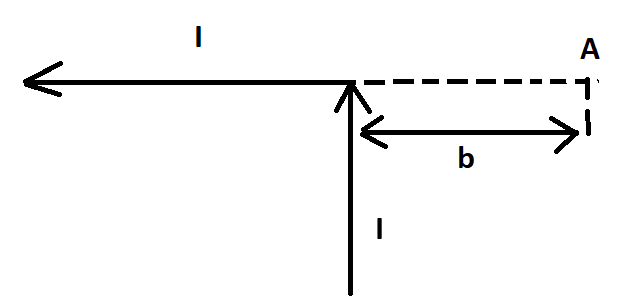
Теперь посмотрим горизонтальный участок, где расположена точка А. Данная область проводника с элементарным током формирует поле в этой точке. Вектор индукции магнитного поля \ равен нулю, потому что в А все углы между с радиус-векторами и с элементарным током равны π.

Следовательно, произведение векторов \\] и поток вектора индукции магнитного поля в законе Био-Савара-Лапласа будет равен нулю:

\}{\mathrm{r}^{3}}\]

В этом случае \ — радиус-вектор, который идет от элемента \ к точке А, в которой находится индукция магнитного поля \.

Индукция бесконечного проводника в точке А была бы равна:

\

Но так как полу бесконечный проводник, то следуя из принципа суперпозиции, получается следующее выражение для проводника магнитной индукций равна:

\

Ответ: \

Как возникает магнитное поле

В начале ХIХ века датский физик Ханс Эрстед и французский исследователь Андре Ампер экспериментально открыли явления, объяснить которые удалось только с помощью введения нового понятия, названного магнитным полем.

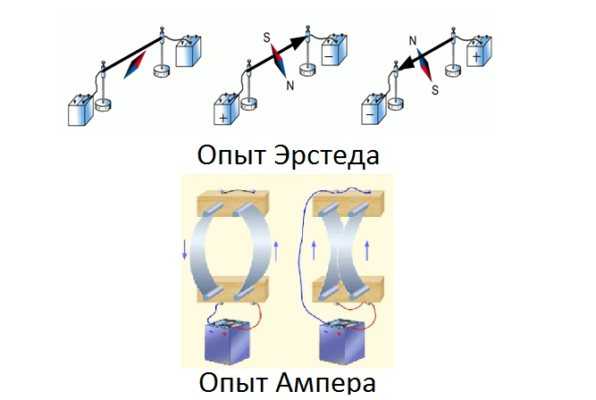
Рис. 1. Опыты Эрстеда и Ампера, демонстрирующие наличие магнитного поля.

Последовавшие вслед за этими опытами многочисленные исследования подтвердили существование нового поля, названного магнитным, которое обладает следующими основными свойствами:

• Магнитное поле возникает только в результате движения электрических зарядов;
• Это поле непрерывно в пространстве и обладает способностью оказывать силовое воздействие на другие электрические заряды, находящиеся в движении;
• Постоянное магнитное поле существует у природных магнитных тел, но и в этом случае причиной возникновения поля является непрерывное движение молекулярных токов (вихрей) в массе вещества;
• Магнитное поле можно создать также с помощью переменного электрического поля.

Ученые недавно узнали, что перелетные птицы ориентируются в пространстве с помощью магнитного поля Земли. У птиц возле глаз имеется небольшой “компас” — небольшое тканевое поле с кристаллами магнетита, которые могут намагничиваться в магнитном поле.

Магнитные полюсы Земли периодически меняются местами!

Да, они это делают, последняя смена была порядка 780000 лет назад (сведения получены на основании анализа горных пород). Хотя иногда процесс происходил чаще. В августе 1999 года началась Эпоха Водолея, вместе с ней грядет очередная смена полюсов. За век вплоть до этой даты магнитный северный полюс смещался ежегодно на 10 км, к началу 2000-х – на целых 50. Цифра постоянно растет. Среди ученых кругов имеются паникеры, утверждающие: переполюсовка каждый раз вызывает крах биосферы: якобы, так погибли динозавры.

Специалисты дают протекающему процессу 40 – 100 лет, потом… физические представления станут верными: стрелка компаса будет смотреть как раз в нужном направлении. Научная интуиция эпохи технической революции? Нельзя сказать точно, но морякам, пилотам пора откорректировать магнитное склонение (разница между направлением на географический и магнитный полюсы). Утешает одно: большинство объектов ориентируется на показания приборов GPS (спутниковая навигация с задействованием земных транслирующих станций).

Изменениями Солнца провоцируются магнитные бури. Природный катаклизм, когда стрелка компаса начинает вести себя непредсказуемо. У поля имеются 11 и 100-летний циклы, мало влияют на погоду, потому незаметны большей части человечества. Скептикам ответим: магнитное поле выступает единственной защитой человечества против действия космического излучения, всерьез пора подумать о сохранности  планеты. Особенно сильно пострадает озоновый слой, вслед за ним – микроскопическое населения океана. Фактически от приспособленности водной жизни к изменениям зависит дальнейшее будущее планеты.

Первый 3-D маппинг поля выполнил спутник Magsat в 1980 году, затем после долгого перерыва в 1999 году проблемой занялся Эрстед (спутник). Необходимость запуска вызвана приходом Эпохи Водолея и описанными выше событиями. Пока исследованием магнитного щита Земли занимается спутниковая группировка Swarm. Считается, что изменения спровоцированы колебаниями состава ядра планеты, ученые хотят найти точные зависимости. После полугода работы (начало 2014 года) результаты исследований стали вызывать озабоченность: магнитное поле ослабевает, меняет конфигурацию.