Булева алгебра

Ассоциативные операции.

Ассоциативными называют операции, которые можно выполнять в
произвольном порядке. По схеме:
(x + y) + z = x + (y + z), где + — некоторая операция.

Здесь приведена программа на языке C,
позволяющая увидеть таблицу истинности всех 16 бинарных логических
операций и проверить их ассоциативность путем перебора вариантов.

Проверка показывает ассоциативность всего лишь для 4 операций
«&», «», «», «» из 10 нетривиальных.

(x & y) & z = x & (y & z)(x y) z = x (y z)(x y) z = x (y z)(x y) z = x (y z)

Из комутативности и ассоциативности этих четырех операций
следует, что если мы имеем много переменных подряд, соединенных
такой операцией, то переменные можно переставлять в любом
порядке, а значит скобки для указания порядка не обязательны:

(a & b) & (c & d) = a & d & c & b.

Функции и законы

Итак, мы уже знаем, какие логические операции использует булева алгебра. Функции описывают все свойства элементов математической логики и позволяют упрощать сложные составные условия задач. Самым понятным и простым кажется свойство отказа от производных операций. Под производными понимаются исключающее ИЛИ, импликация и эквивалентность. Поскольку мы ознакомились только с основными операциями, то и свойства рассмотрим тоже только их.

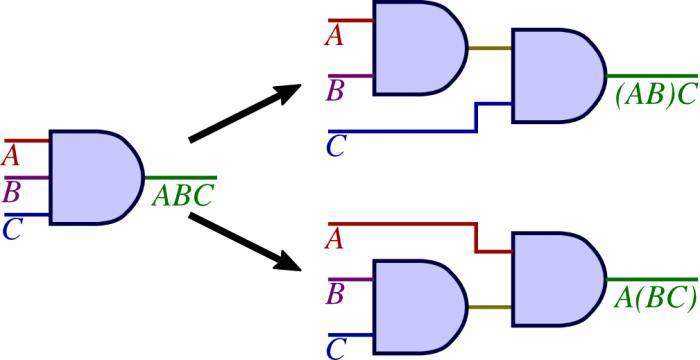
Ассоциативность означает, что в высказываниях типа «и А, и Б, и В» последовательность перечисления операндов не играет роли. Формулой это запишется так:

(A∧Б)∧В=A∧(Б∧В)=A∧Б∧В,

(A∨Б)∨В=A∨(Б∨В)=A∨Б∨В.

Как видим, это свойственно не только конъюнкции, но и дизъюнкции.

Коммутативность утверждает, что результат конъюнкции или дизъюнкции не зависит от того, какой элемент рассматривался вначале:

A∧Б=Б∧A; A∨Б=Б∨A.

Дистрибутивность позволяет раскрывать скобки в сложных логических выражениях. Правила схожи с раскрытием скобок при умножении и сложении в алгебре:

A∧(Б∨В)=A∧Б∨A∧В; A∨Б∧В=(A∨Б)∧(A∨В).

Свойства единицы и нуля, которые могут быть одним из операндов, также аналогичны алгебраическим умножению на ноль или единицу и сложению с единицей:

A∧0=0,A∧1=A; A∨0=A,A∨1=1.

Идемпотентность говорит нам о том, что если относительно двух равных операндов результат операции оказывается аналогичным, то можно «выбросить» лишние усложняющие ход рассуждений операнды. И конъюнкция, и дизъюнкция являются идемпотентными операциями.

Б∧Б=Б; Б∨Б=Б.

Поглощение также позволяет нам упрощать уравнения. Поглощение утверждает, что когда к выражению с одним операндом применяется другая операция с этим же элементом, результатом оказывается операнд из поглощающей операции.

A∧Б∨Б=Б; (A∨Б)∧Б=Б.

Логическая функция «И» (умножение)

Функция логики И утверждает, что два или более события должны происходить вместе и одновременно, чтобы происходило выходное действие. Порядок, в котором происходят эти действия, не имеет значения, поскольку он не влияет на конечный результат. Например, & B = B & . В булевой алгебре функция логики И подчиняется коммутативному закону, который допускает изменение положения любой переменной.

Функция «И» представлена в электронике символом точки или полной остановки ( . ) Таким образом, 2-входное ( АВ ) «И» элемент имеет выходной термин, представленный логическим выражением A.B или просто AB.

Представление функции «И» на схеме

Здесь два переключателя A и B соединены вместе, образуя последовательную цепь. Поэтому в вышеупомянутой цепи оба выключателя A «И» B должны быть замкнуты (логика «1»), чтобы включить лампу. Другими словами, оба переключателя должны быть замкнуты или должны иметь логическую «1», чтобы лампа горела.

Тогда логический элемент этого типа (логический элемент «И» ) создает выход только тогда, когда все его входы истины. В терминах булевой алгебры вывод будет ИСТИНА, только когда все его входы ИСТИНА. В электрическом смысле логическая функция «И» равна последовательной цепи, как показано выше.

Поскольку имеется только два переключателя, каждый с двумя возможными состояниями «открытый» или «закрытый». Определяя логическую «0» как то, когда переключатель разомкнут, и логическую «1», когда переключатель замкнут, существует четыре различных способа или комбинации расположения двух переключателей вместе, как показано в таблице ниже.

Таблица истинности для функции «И»

Логические «И» элементы доступны как стандартные пакеты ic, такие как общие TTL 74LS08 Четырехпозиционные 2-входные положительные элементы «И» (или эквивалент CMOS 4081), TTL 74LS11 Тройные 3-входные положительные элементы «И» или 74LS21 Двойные 4-входные положительные элементы «И». «И» ворота можно также «каскадировать» вместе для создания цепей с более чем 4 входами.

Алгебра логики

Алгебра логики, или булева алгебра, – это раздел математики, возникший в XIX веке благодаря работам английского математика Джорджа Буля. Поначалу булева алгебра не имела практического значения. Однако уже в XX веке ее положения нашли применение в описании функционирования и разработке различных электронных схем.

Законы и аппарат алгебры логики стали применяться при проектировании различных частей компьютеров, в частности памяти и процессора. Хотя это не единственная сфера применения данной науки.

Что же собой представляет алгебра логики? Во-первых, она изучает методы определения истинности или ложности сложных логических высказываний с помощью алгебраических методов.

Во-вторых, булева алгебра делает это таким образом, что сложное логическое высказывание описывается функцией, результатом вычисления которой может быть либо истина, либо ложь. Истине сопоставляется 1, лжи – 0. При этом аргументами функций выступают простые высказывания, которые также могут иметь только два значения – 0 или 1.

Фразы «два больше одного», «5.8 является целым числом» будем считать примерами простых логических высказываний. Анализируя эти высказывания, мы делаем вывод, что первая фраза правдивая, вторая – ложная. Это и есть результат выполнения простого логического выражения.

Алгебра логики не касается сути высказываний. Она занимается вычислениями результата сложных логических высказываний на основе заранее известных значений простых высказываний.

Определение

Булева алгебра является шести- кортеж , состоящий из множества A , оснащен двумя бинарными операциями ∧ ( так называемые «концами» или «и»), ∨ ( так называемый «присоединиться» или «или»), А унарная операция ¬ ( так называемый » дополнять или не дополнять) и два элемента 0 и 1 в A (называемые «нижний» и «верхний», или «наименьший» и «наибольший» элементы, также обозначаемые символами ⊥ и ⊤ соответственно), такие, что для Для всех элементов a , b и c из A верны следующие аксиомы

a ∨ ( b ∨ c ) = ( a ∨ b ) ∨ c	a ∧ ( b ∧ c ) = ( a ∧ b ) ∧ c	ассоциативность
а ∨ б = б ∨ а	а ∧ б = б ∧ а	коммутативность
а ∨ ( а ∧ б ) = а	а ∧ ( а ∨ б ) = а	поглощение
а ∨ 0 = а	а ∧ 1 = а	идентичность
a ∨ ( b ∧ c ) = ( a ∨ b ) ∧ ( a ∨ c )	a ∧ ( b ∨ c ) = ( a ∧ b ) ∨ ( a ∧ c )	распределенность
а ∨ ¬ а = 1	а ∧ ¬ а = 0	дополняет

Обратите внимание, однако, что закон поглощения и даже закон ассоциативности могут быть исключены из набора аксиом, поскольку они могут быть получены из других аксиом (см. ).

Булева алгебра, содержащая только один элемент, называется тривиальной булевой алгеброй или вырожденной булевой алгеброй

(В более старых работах некоторые авторы требовали, чтобы 0 и 1 были отдельными элементами, чтобы исключить этот случай.)

Булева алгебра, содержащая только один элемент, называется тривиальной булевой алгеброй или вырожденной булевой алгеброй . (В более старых работах некоторые авторы требовали, чтобы 0 и 1 были отдельными элементами, чтобы исключить этот случай.)

Из трех последних пар аксиом выше (тождество, дистрибутивность и дополнения) или из аксиомы поглощения следует, что

a = b ∧ a     тогда и только тогда, когда     a ∨ b = b .

Отношение ≤, определяемое как a ≤ b, если эти эквивалентные условия выполняются, является частичным порядком с наименьшим элементом 0 и наибольшим элементом 1. Встреча a ∧ b и соединение a ∨ b двух элементов совпадают с их точной гранью и супремумом соответственно, относительно ≤.

Первые четыре пары аксиом составляют определение ограниченной решетки .

Из первых пяти пар аксиом следует, что любое дополнение единственно.

Набор аксиом самодвойственен в том смысле, что если заменить ∨ на и 0 на 1 в аксиоме, результатом снова будет аксиома. Следовательно, применяя эту операцию к булевой алгебре (или булевой решетке), можно получить другую булеву алгебру с теми же элементами; это называется его двойственным .

Таблицы и операции

Построить таблицу истинности можно без онлайн калькуляторов. Для этого достаточно запомнить, как работает каждая из перечисленных выше операций. У математиков с этим проблем не возникает – они хорошо заучивают предложенную далее информацию.

Конъюнкция

Носит название «логическое И» или «умножение». Часто встречается в программировании. В языках «создания контента» обладает особым обозначением. Примеры записи:

• И;
• AND;
• &;
• &&.

Выражение логического характера при конъюнкции является истиной, только когда оба простых высказывания тоже выступают в качестве правды. Если хотя бы одно из них – ложь, то вся операция примет значение False.

Выше представлена таблица истинности при операции конъюнкции.

Дизъюнкция

Является сложением. У этого логического выражения есть иное название – «логическое ИЛИ». Тоже встречается в программировании довольно часто.

Может иметь такие формы записи:

• ||;
• ИЛИ;
• OR;
• |.

Преобразование последовательности будет осуществляться по принципу: выражение – истина, если хотя бы одно из его составляющих – правда. Ложно, когда оба элемента имеют значение FALSE.

Выше – примеры таблицы истинности, которая работает в отношении дизъюнкции.

Инверсия

Следующий момент, на который стоит обратить внимание – это инверсия. Носит название «отрицание» или «логическое НЕ»

Обозначения в программировании:

• НЕ;
• !;
• NOT.

Логическое выражение при отрицании обладает следующими особенностями:

1. Когда исходные данные истины, то результатом станет ложь.
2. Если операция обладает значением «ложь», ее отрицание получит «истину».
3. Можно рассматривать соответствующую манипуляцию как трактовку «Неверно, что…»

Вот такую таблицу истинности можно построить относительно инверсии.

Импликация

При любом логическом выводе стоит опираться на предлагаемые примеры и таблицы. Импликация – это следование.

В любом заданном логическом выражении результат – это истина всегда. Исключение – когда из правды следует ложь. Она связывает два высказывания (a и b), где:

• A – это условие, первое выражение;
• B – следствие.

Если из A может следовать B, значит операция выдаст в результате обработки «истину».

Эквивалентность

Так называют равнозначность. Новое высказывание истинно тогда, когда оба простых выражения – это правда.

Выше – пример расчетов формулы логики заданных высказываний при эквивалентности.

Исключение

Онлайн калькуляторы могут помочь построить график или указать, что верно, а что нет, без вдумчивости в поставленную задачу со стороны пользователя. Но программистам приходится прописывать принципы функционирования и выполняемые операции вручную. Для них особенности алгебры логики и информатики крайне важны.

Порядок выполнения логических операций ранее был рассмотрен. Осталось понять, как работает исключение.

Согласно установленным правилам, операция будет истиной, когда среди значений переменных A и B есть одно правдивое. Если оба – это действительность, упомянутый принцип работать не будет.

Исключающее ИЛИ – преобразование, которое носит название «сложение по модулю два».

Проверь себя

Задание 1.Для выражения А ∨ В ∧ ¬(В ∧ А) выберите верную запись на языке Python (с сохранением порядка действий):

1. A and B or not B or A
2. A and B or not (B or A)
3. A or B and not B and A
4. A or B and not (B and A)

Задание 2.Для выражения ¬А ⇒ В ≡ А ∧ В выберите верную запись на языке Python (с сохранением порядка действий):

1. not (А <= В == А and В)
2. not А <= В == (А and В)
3. ((not A) <=  B) == (A and B)
4. (not А) <= (В == (А and В))

Задание 3.Чему будет равен последний столбец таблицы истинности для уравнения: A ∧ B ⇒ C ∧ D ∨ D ∧ A?

1. 11101101
2. 11101111
3. 00000011
4. 11000111

Задание 4.Выберите уравнение, которое во всех случаях принимает значение истины:

1. ¬(A ∧ B) ∧ ¬(C ∧ ¬A)
2. ¬(A ∧ B) ∨ ¬(C ∧ ¬A)
3. A ∧ B ∧ ¬(C ∧ ¬A)
4. ¬(A ∧ B) ∨ ¬(C ∧ A)

Ответ: 1. — 4; 2. — 3; 3. — 1; 4. — 2.

Сравнительные операторы

В программировании сравнительные операторы используются для сравнения значений и оценки значения отдельного булева значения true или false.

В таблице ниже показаны булевы операторы сравнения.

Оператор	Значение
==	равно
! =	не равно
<	меньше
>	больше
<=	меньше или равно
>=	больше или равно

Чтобы понять принцип работы этих операторов, присвоим два целочисленных значения двум переменным в программе Go:

Поскольку в этом примере имеет значение , эта переменная меньше со значением .

Используем эти две переменные и их значения для проверки операторов из предыдущей таблицы. В этой программе вы предписываете Go вывести результат true или false для каждого оператора сравнения. Чтобы лучше понять результат, укажите Go распечатать строку, чтобы показывать, что именно оценивается:

Следуя математической логике, Go оценивает выражения следующим образом:

• 5 () равно 8 ()? false
• 5 не равно 8? true
• 5 меньше 8? true
• 5 больше 8? false
• 5 меньше или равно 8? true
• 5 не меньше или равно 8? false

Хотя здесь использовались целые числа, вы можете заменить их значениями с плавающей точкой.

Также с булевыми операторами можно использовать строки. Они учитывают регистр, если вы не используете дополнительный метод строки.

Вы можете посмотреть практический пример сравнения строк:

Строка не равна строке , поскольку они не точно совпадают; одно значение начинается с заглавной , а другое — с в нижнем регистре. Однако если вы добавите другую переменную, которой присвоено значение , они будут равняться:

Также вы можете использовать для сравнения двух строк и другие операторы сравнения, в том числе и . Go проводит лексикографическое сравнение строк, используя значения ASCII для символов.

Также вы можете оценить булевы значения с помощью операторов сравнения:

Предыдущий блок кода оценил, что не равняется .

Обратите внимание на различия между операторами и. Первый оператор является оператором присвоения, который задает одно значение равным другому. Второй оператор является оператором сравнения и оценивает, что два значения будут равны

Второй оператор является оператором сравнения и оценивает, что два значения будут равны

Первый оператор является оператором присвоения, который задает одно значение равным другому. Второй оператор является оператором сравнения и оценивает, что два значения будут равны.

Операции булевой алгебры

Мы уже помним, что операции в алгебре суждений – логические. Подобно тому, как алгебра чисел использует арифметические операции для сложения, вычитания или сравнения чисел, элементы математической логики позволяют составить сложные высказывания, дать отрицание или вычислить конечный результат.

Логические операции для формализации и простоты записываются формулами, привычными для нас в арифметике. Свойства булевой алгебры дают возможность записывать уравнения и вычислять неизвестные. Логические операции обычно записывают с помощью таблицы истинности. Её столбцы определяют элементы вычислений и операцию, которая над ними производится, а строки показывают результат вычислений.

↑тНПЛСКХПНБЙЮ НЯМНБМШУ РЕНПЕЛ щ. оНЯРЮ

гЮЛЙМСРШЕ ЙКЮЯЯШ АСКЕБШУ ТСМЙЖХИ АШКХ НОХЯЮМШ ЮЛЕПХЙЮМЯЙХЛ ЛЮРЕЛЮРХЙНЛ щ. к.  оНЯРНЛ Б 1920 ЦНДС. нМ ХГСВХК ПЪД БЮФМШУ ЯБНИЯРБ ЩРХУ ЙКЮЯЯНБ. нЯМНБМШЕ ПЕГСКЭРЮРШ оНЯРЮ ТНПЛСКХПСЧРЯЪ ЯКЕДСЧЫХЛ НАПЮГНЛ.

оСЯРЭ F — ОПНХГБНКЭМШИ ГЮЛЙМСРШИ ЙКЮЯЯ АСКЕБШУ ТСМЙЖХИ, Ю A — МЕЙНРНПЮЪ ЯХЯРЕЛЮ ТСМЙЖХИ, ЯНДЕПФЮЫХУЯЪ Б F. цНБНПЪР, ВРН ЯХЯРЕЛЮ A ОНПНФДЮЕР ГЮЛЙМСРШИ ЙКЮЯЯ F, ЕЯКХ = F. б ЩРНЛ ЯКСВЮЕ ЦНБНПЪР РЮЙФЕ, ВРН ЯХЯРЕЛЮ A ЪБКЪЕРЯЪ ОНКМНИ Б F. аЮГХЯНЛ ЙКЮЯЯЮ F МЮГШБЮЕРЯЪ РЮЙЮЪ ОНПНФДЮЧЫЮЪ F ЯХЯРЕЛЮ A, КЧАЮЪ ЯНАЯРБЕММЮЪ ОНДЯХЯРЕЛЮ ЙНРНПНИ МЕ ОНПНФДЮЕР F. яОПЮБЕДКХБШ ЯКЕДСЧЫХЕ ДБЮ ОПХМЮДКЕФЮЫХУ щ. оНЯРС СРБЕПФДЕМХЪ: ЛМНФЕЯРБН БЯЕУ ГЮЛЙМСРШУ ЙКЮЯЯНБ ТСМЙЖХИ ЮКЦЕАПШ КНЦХЙХ ХЛЕЕР ЯВ╦РМСЧ ЛНЫМНЯРЭ; ЙЮФДШИ ГЮЛЙМСРШИ ЙКЮЯЯ АСКЕБШУ ТСМЙЖХИ ХЛЕЕР ЙНМЕВМШИ АЮГХЯ.

оНЯР НОХЯЮК РЮЙФЕ ОНКМСЧ ДХЮЦПЮЛЛС БЙКЧВЕМХИ ЛМНФЕЯРБЮ БЯЕУ ГЮЛЙМСРШУ ЙКЮЯЯНБ АСКЕБШУ ТСМЙЖХИ.

Законы алгебры логики

Исключение констант	\( 1 + A = 1 \)\( 0 ⋅ A = 0 \)\( 0 + A = A \)\( 1 ⋅ A = A \)
Идемпотентность	\( A + A = A \)\( A ⋅ A = A \)
Закон исключения третьего	\( A + \overline{A} = 1 \)
Закон непротиворечивости	\( A ⋅ \overline{A} = 0 \)
Закон отрицания	\( \overline{\overline{A}} = A \)
Закон коммутативности	\( A + B = B + A \)\( A ⋅ B = B ⋅ A \)
Закон ассоциативности	\( A + B + C = A + (B + C)\)\( A ⋅ B ⋅ C = A ⋅ (B ⋅ C)\)
Закон дистрибутивности	\( A ⋅ (B + C) = A ⋅ B + A ⋅ C \)\( A + (B ⋅ C) = (A + B) ⋅ (A + C) \)
Правило де Моргана	\( \overline{(A + B)} = \overline{A} ⋅ \overline{B}\)\( \overline{(A ⋅ B)} = \overline{A} + \overline{B}\)
Закон поглощения	\( A + A ⋅ B = A\)\( A ⋅ (A + B) = A\)
Закон склеивания	\( A ⋅ B + \overline{A} ⋅ B = B \)\( (A + B) ⋅ (\overline{A} + B) = B \)

Законы алгебры можно доказать составив таблицу истинности.

Некоторые свойства[]

Из аксиом видно, что наименьшим элементом является 0, наибольшим является 1, а дополнение ¬a любого элемента a однозначно определено. Для всех a и b из A верны также следующие равенства:

a∨a=a{\displaystyle a\lor a=a}	a∧a=a{\displaystyle a\land a=a}
a∨=a{\displaystyle a\lor 0=a}	a∧1=a{\displaystyle a\land 1=a}
a∨1=1{\displaystyle a\lor 1=1}	a∧={\displaystyle a\land 0=0}
¬=1{\displaystyle \lnot 0=1}	¬1={\displaystyle \lnot 1=0}	дополнение 0 есть 1 и наоборот
¬(a∨b)=¬a∧¬b{\displaystyle \lnot (a\lor b)=\lnot a\land \lnot b}	¬(a∧b)=¬a∨¬b{\displaystyle \lnot (a\land b)=\lnot a\lor \lnot b}	законы де Моргана
¬¬a=a{\displaystyle \lnot \lnot a=a}		инволютивность отрицания

Дистрибутивные операции.

Дистрибутивной называют пару операций, для которых
работает схема раскрытия скобок, характерная для
сложения и умножения в арифметике:

x * (y + z) = (x * y) + (x * z) и
(x + y) * z = (x * z) + (y * z),
где * и + — некоторые
логические операции.

Первую схему будем называть левой дистрибутивностью, вторую
схему — правой дистрибутивностью, а если срабатывают обе
схемы, то будем говорить о полной дистрибутивности или просто
дистрибутивности.

Здесь приведена программа на языке C, позволяющая проверить
дистрибутивность для всех возможных комбинаций бинарных
логических операций путем перебора вариантов. Она автоматически
пропускает тривиальные операции и составляет правила
дистрибутивности.

Результаты программы выглядят так.

Из полученных правил наибольший практический интерес
представляют:

x & (y z) = (x & y) (x & z)(x y) & z = (x & z) (y & z)x (y & z) = (x y) & (x z)(x & y) z = (x z) & (y z)x & (y z) = (x & y) (x & z)(x y) & z = (x & z) (y & z)

Как видите, дистрибутивность между логическим умножением
и сложением в алгебре логики такая же как в обычной
алгебре (где она называется «распределительным законом»).
Обратите внимание, что и для операций «» и «&» можно
раскрывать скобки таким же способом. Причем обе операции
оказываются равноправны: можно раскрывать скобки когда
в них стоит «&», а вне скобок — «», а можно и в обратной
ситуации — когда внутри скобок стоит «»

Дистрибутивные операции.

Дистрибутивной называют пару операций, для которых
работает схема раскрытия скобок, характерная для
сложения и умножения в арифметике:

x * (y + z) = (x * y) + (x * z) и
(x + y) * z = (x * z) + (y * z),
где * и + — некоторые
логические операции.

Первую схему будем называть левой дистрибутивностью, вторую
схему — правой дистрибутивностью, а если срабатывают обе
схемы, то будем говорить о полной дистрибутивности или просто
дистрибутивности.

Здесь приведена программа на языке C, позволяющая проверить
дистрибутивность для всех возможных комбинаций бинарных
логических операций путем перебора вариантов. Она автоматически
пропускает тривиальные операции и составляет правила
дистрибутивности.

Результаты программы выглядят так.

Из полученных правил наибольший практический интерес
представляют:

x & (y z) = (x & y) (x & z)(x y) & z = (x & z) (y & z)x (y & z) = (x y) & (x z)(x & y) z = (x z) & (y z)x & (y z) = (x & y) (x & z)(x y) & z = (x & z) (y & z)

Как видите, дистрибутивность между логическим умножением
и сложением в алгебре логики такая же как в обычной
алгебре (где она называется «распределительным законом»).
Обратите внимание, что и для операций «» и «&» можно
раскрывать скобки таким же способом. Причем обе операции
оказываются равноправны: можно раскрывать скобки когда
в них стоит «&», а вне скобок — «», а можно и в обратной
ситуации — когда внутри скобок стоит «»

Прежде всего, начнем с разбора названия самого предмета, а именно выясним, каково значение алгебры, логики, а затем алгебры логики.

Алгебра – это раздел математики, предназначенный для описания действий над переменными величинами, которые принято обозначать строчными буквами латинского алфавита – а, b, x, y и т.д. Действия над переменными величинами записываются в виде математических выражений.

Термин «логика» происходит от древнегреческого “logos”, означающего «слово, мысль, понятие, рассуждение, закон».

Алгеброй логики называется аппарат, который позволяет выполнять действия над высказываниями.

Алгебру логику называют также алгеброй Буля, или булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего в XIX веке ее основные положения. В булевой алгебре высказывания принято обозначать прописными латинскими буквами: A, B, X, Y. В алгебре Буля введены три основные логические операции с высказываниями? Сложение, умножение, отрицание. Определены аксиомы (законы) алгебры логики для выполнения этих операций. Действия, которые производятся над высказываниями, записываются в виде логических выражений.

Логические выражения могут быть простыми и сложными.

Простое логическое выражение состоит из одного высказывания и не содержит логические операции. В простом логическом выражении возможно только два результата — либо «истина», либо «ложь».

Сложное логическое выражение содержит высказывания, объединенные логическими операциями. По аналогии с понятием функции в алгебре сложное логическое выражение содержит аргументы, которыми являются высказывания.

В качестве основных логических операций в сложных логических выражениях используются следующие:

• НЕ (логическое отрицание, инверсия);

• ИЛИ (логическое сложение, дизъюнкция);

• И (логическое умножение, конъюнкция).

Логическое отрицание является одноместной операцией, так как в ней участвует одно высказывание. Логическое сложение и умножение — двуместные операции, в них участвует два выска¬зывания. Существуют и другие операции, например операции следования и эквивалентности, правило работы которых можно вывести на основании основных операций.

Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении, например:

• таблица истинности одноместной логической операции состоит из двух строк: два различных значения аргумента — «истина» (1) и «ложь» (0) и два соответствующих им значения функции;
• в таблице истинности двуместной логической операции — четыре строки: 4 различных сочетания значений аргументов — 00, 01, 10 и 11 и 4 соответствующих им значения функции;
• если число высказываний в логическом выражении N, то таблица истинности будет содержать 2 N строк, так как существует 2 N различных комбинаций возможных значений аргументов.

Приложения

Его основным сценарием применения является цифровая ветвь, где он служит для структурирования схем, составляющих задействованные логические операции. Искусство упрощения схем для оптимизации процессов — результат правильного применения и практики булевой алгебры.

От разработки электрических панелей, передачи данных до программирования на разных языках, мы часто можем найти булеву алгебру во всех видах цифровых приложений.

Логические переменные очень часто встречаются в структуре программирования. В зависимости от используемого языка программирования в коде будут структурные операции, использующие эти переменные. Условные выражения и аргументы каждого языка допускают логические переменные для определения процессов.

Связь с естественным языком

Часто указывают на сходство между конъюнкцией и союзом «и» в естественном языке. Составное утверждение «A и B» считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как {\displaystyle 0}. При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз «и» может нести дополнительный оттенок «и тогда», «и поэтому», «и потом». Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке «Мэри вышла замуж и родила ребёнка» — не то же самое, что «Мэри родила ребёнка и вышла замуж».