Общее описание
Физически электронное устройство — конденсатор — представляет собой две обкладки, выполненные из проводящего материала, между которыми находится диэлектрический слой. С поверхности пластин выводятся два электрода, предназначенные для подключения в электрическую цепь. Конструктивно прибор может быть различного размера и формы, но его структура остаётся неизменной, то есть всегда происходит чередование проводящего и диэлектрического слоев.
Слово «конденсатор» произошло от латинского «condensatio» — «накопление». Научное определение гласит, что накопительный электрический прибор — это двухполюсник, характеризующийся постоянным и переменным значениями ёмкости и большим сопротивлением. Предназначен он для накопления энергии и заряда. За единицу измерения ёмкости принят фарад (F).
Принцип действия конденсатора заключается в следующем: при включении прибора в электрическую цепь напряжение в ней будет иметь нулевую величину. В этот момент устройство начинает получать и накапливать заряд. Электрический ток, подающийся в схему, будет максимально возможным. Через некоторое время на одном из электродов прибора начнут накапливаться заряды положительного знака, а на другом — отрицательного.
Длительность этого процесса зависит от ёмкости прибора и активного сопротивления. Расположенный между выводами диэлектрик мешает перемещению частиц между обкладками. Но это будет происходить лишь до того момента, пока разность потенциалов источника питания и напряжение на выводах конденсатора не сравняются. В этот момент ёмкость станет максимально возможной, а электроток — минимальным.
Если на элемент перестают подавать напряжение, то при подключении нагрузки конденсатор начинает отдавать свой накопленный заряд ей. Его ёмкость уменьшается, а в цепи снижаются уровни напряжения и тока. Иными словами, накопительный прибор сам превращается в источник питания. Поэтому если конденсатор подключить к переменному току, то он начнёт периодически перезаряжаться, то есть создавать определённое сопротивление в цепи.
Общее описание
Физически электронное устройство — конденсатор — представляет собой две обкладки, выполненные из проводящего материала, между которыми находится диэлектрический слой. С поверхности пластин выводятся два электрода, предназначенные для подключения в электрическую цепь. Конструктивно прибор может быть различного размера и формы, но его структура остаётся неизменной, то есть всегда происходит чередование проводящего и диэлектрического слоев.
Слово «конденсатор» произошло от латинского «condensatio» — «накопление». Научное определение гласит, что накопительный электрический прибор — это двухполюсник, характеризующийся постоянным и переменным значениями ёмкости и большим сопротивлением. Предназначен он для накопления энергии и заряда. За единицу измерения ёмкости принят фарад (F).
Принцип действия конденсатора заключается в следующем: при включении прибора в электрическую цепь напряжение в ней будет иметь нулевую величину. В этот момент устройство начинает получать и накапливать заряд. Электрический ток, подающийся в схему, будет максимально возможным. Через некоторое время на одном из электродов прибора начнут накапливаться заряды положительного знака, а на другом — отрицательного.
Длительность этого процесса зависит от ёмкости прибора и активного сопротивления. Расположенный между выводами диэлектрик мешает перемещению частиц между обкладками. Но это будет происходить лишь до того момента, пока разность потенциалов источника питания и напряжение на выводах конденсатора не сравняются. В этот момент ёмкость станет максимально возможной, а электроток — минимальным.
Если на элемент перестают подавать напряжение, то при подключении нагрузки конденсатор начинает отдавать свой накопленный заряд ей. Его ёмкость уменьшается, а в цепи снижаются уровни напряжения и тока. Иными словами, накопительный прибор сам превращается в источник питания. Поэтому если конденсатор подключить к переменному току, то он начнёт периодически перезаряжаться, то есть создавать определённое сопротивление в цепи.
Принцип работы конденсатора
Подключение прибора к постоянному источнику приводит к тому, что в начальный момент происходит аккумуляция в обкладках из-за электростатической индукции, а сопротивление в этот момент приравнивается нулю. Электрическая индукция провоцирует поле к притяжению разноимённых зарядов на разные обкладки, расположенные друг напротив друга.
Вам это будет интересно Все о бесперебойном питании
Такое свойство получило название ёмкость, которая характерна для всех типов материалов, в том числе и диэлектриков, однако в случае с проводниками она существенно больше. Именно поэтому обкладки изготавливаются из проводника. Увеличение ёмкости способствует накоплению большего количества зарядок на обкладках.
Важно! Когда аккумулируются заряды, происходят ослабление поля и наращивание двухполюсника. Принцип работы
Принцип работы
Происходит это из-за уменьшения места в обкладках, воздействия одноимённых зарядов друг на друга. Одновременно с этим напряжение приравнивается к источнику тока. Прекращение электричества в цепи происходит после того, когда обкладки полностью заполнятся электричеством. Из-за этого пропадает индукция и остаётся только поле, удерживающее и не пропускающее заряды.
Диэлектрик между обкладками
Электротоку будет некуда деться, а на двухполюснике напряжение приравнивается к ЭДС. Когда ЭДС повышается, поле сильнее воздействует на диэлектрик из-за отсутствия места в обкладках. Если внутреннее конденсаторное напряжение будет выше предельных значений, тогда пробьёт диэлектрик.
Конденсатор преобразуется в проводник, и происходит освобождение зарядов, из-за чего электроток начинает идти. Чтобы применять двухполюсник при высоком напряжении повышают размер диэлектрика и наращивают расстояние, имеющееся между обкладками на фоне снижения ёмкости. Диэлектрик располагается между обкладками и не даёт проходить постоянному, выполняя в отношении него барьерную функцию.
Электрическая индукция
Обратите внимание! Именно постоянное напряжение способно формировать электростатическую индукцию, но только в случае замыкания в момент зарядки конденсатора. Благодаря этому механизму сохраняется энергия до момента подсоединения к нему потребителю
Конденсатор в цепи постоянного тока
Чтобы понять, как работает накопитель в цепи постоянного тока, надо добавить в схему лампочку, которая станет загораться только при зарядке, в процессе которой от электротока остаётся напряжение, как бы догоняющее его из-за плавного нарастания. Заряды электричества затрачивают какое-то время для перемещения к обкладкам, именно это и есть время зарядки, продолжительность которого определяется частотой и ёмкостью напряжения. Когда зарядка завершается, лампочка тухнет, и постоянный электроток перестаёт проходить через пассивный электронный компонент.
Конденсатор в цепи переменного тока
Если у источника изменить полярность, то это приведёт к разрядке конденсатора в цепи переменного тока и его повторной зарядке. Формируется постоянная электростатическая индукция при переменном. Всегда при изменении электричеством своего направления запускается механизм зарядки и разрядки, из-за чего он и пропускает переменный. Увеличение частоты приводит к снижению ёмкостного сопротивления двухполюсника.
Вам это будет интересно Монтаж и подключение теплого пола
Конденсатор в постоянной цепи
Емкостное сопротивление конденсатора
Конденсаторы относятся к наиболее распространенным элементам, используемым в различных электронных схемах. Они разделяются на типы, обладающие характерными особенностями, параметрами и индивидуальными свойствами. Простейший конденсатор состоит из двух металлических пластин – электродов, разделенных слоем диэлектрика. На каждом из них имеется собственный вывод, через который осуществляется подключение к электрической цепи.
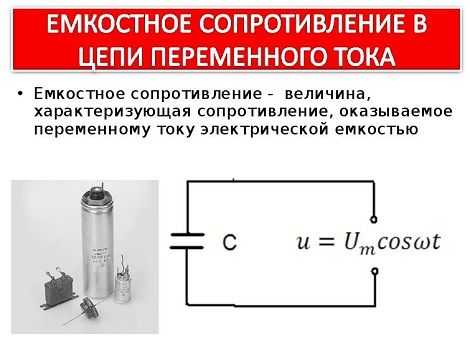
Существуют качества, присущие только конденсаторам. Например, они совершенно не пропускают через себя постоянный ток, хотя и заряжаются от него. После полной зарядки емкости, течение тока полностью прекращается, а внутреннее сопротивление устройства принимает бесконечно высокое значение.
Совершенно по-другому на конденсатор воздействует переменный ток, вполне свободно протекающий через емкость. Подобное состояние объясняется постоянными процессами зарядки-разрядки элемента. В этом случае действует не только активное сопротивление проводников, но и емкостное сопротивление самого конденсатора, возникающее как раз в результате его постоянной зарядки и разрядки.
Электрические параметры и свойства конденсаторов могут отличаться, в зависимости от различных факторов. В первую очередь они зависят от размеров и формы изделия, а также от типа диэлектрика. В разных типах устройств диэлектриком может служить бумага, воздух, пластик, стекло, слюда, керамика и другие материалы. В электролитических конденсаторах используются алюминий-электролит и тантал-электролит, что обеспечивает им повышенную емкость.
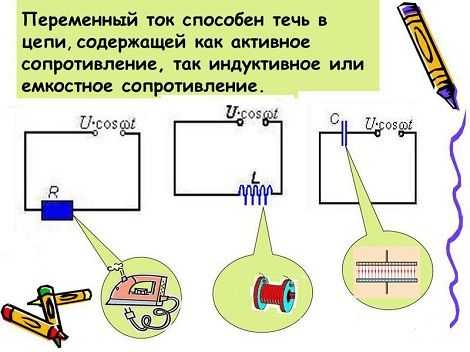
Названия других элементов определяются материалами обычных диэлектриков. Поэтому они относятся к категории бумажных, керамических, стеклянных и т.д. Каждый из них, в соответствии с характеристиками и особенностями, применяется в конкретных электронных схемах, с разными параметрами электротока.
В связи с этим, применение керамических конденсаторов необходимо в тех цепях, где требуется фильтрация высокочастотных помех. Электролитические устройства, наоборот, фильтруют помехи при низких частотах. Если же соединить параллельно оба типа конденсаторов, получится универсальный фильтр, широко применяемый во всех схемах. Несмотря на то, что их емкость является фиксированной величиной, существуют устройства с переменной емкостью, которая достигается путем регулировок за счет изменение взаимного перекрытия пластин. Типичным примером служат конденсаторы для подстройки, используемые при регулировке радиоэлектронной аппаратуры.
Применение на практике
Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:
- Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора. Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
- Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.
В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда. В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.
Благодаря своим свойствам конденсаторы используются в тех случаях, когда необходимо передать и постоянный, и переменный ток по одним и тем же проводам. Источник постоянного напряжения подключается к общему проводу и второму выводу ёмкости, через которую присоединяется источник переменного напряжения. На другой стороне происходит разделение: потребитель переменного подключается через конденсатор той же ёмкости, а потребитель постоянного — напрямую, до выводов детали.
Задачи на переменный электрический ток
Прежде, чем мы перейдем непосредственно к примерам решения задач на переменный ток, скажем кое-что для тех, кто вообще не знает, с какой стороны подступиться к задачам по физике. У нас есть универсальный ответ – памятка по решению. А еще, вам могут пригодиться формулы.
Хотите разобраться в теории? Читайте в нашем блоге, что такое фаза и ноль в электричестве.
Задача№1. Переменный ток
Условие
Вольтметр, включённый в цепь переменного тока,показывает напряжение 220 В, а амперметр – ток 10 А.Чему равны амплитудные значения измеряемых величин?
Решение
Амперметр показывает мгновенные, действующие значения величин. Действующие значения силы тока и напряжения меньше амплитудных в 2 раз. Исходя из этого, рассчитаем:
IA=Iд·2=10·2=14,1 АUA=Uд·2=220·2=311 В
Ответ: 14,1 А; 311 В.
Задача№2. Переменный ток
Условие
Рамка вращается в однородном магнитном поле. ЭДС индукции, возникающая в рамке, изменяется по закону e=80sin25πt. Определите время одного оборота рамки.
Решение
Из условия можно найти угловую частоту вращения рамки:
e=εmsinωte=80sin25πtω=25π радс
Время одного оборота рамки – это период колебаний, связанный с угловой частотой:
T=2πω=2π25π=,08 с
Ответ: 0,08 с.
Больше задач на тему ЭДС в нашем блоге.
Задача№3. Переменный ток
Условие
Сила тока в колебательном контуре изменяется по закону I =0,4sin(400πt) (А). Определите емкосьть конденсатора в контуре, если индуктивность катушки равна 125 мГн.
Решение
Запишем закон изменения силы тока в контуре:
I=IAsinωt
Учитывая исходное уравнение, можно найти угловую частоту и период колебаний:
ω=400π радс
T=2πω=2π400π=5·10-3c
Емкость конденсатора найдем из формулы Томпсона:
T=2πLCT2=4π2LCC=T24π2L=25·10-64·9,85·125·10-3=5·10-6 Ф
Ответ: 5 мкФ.
Задача№4. Переменный ток
Условие
Чему равна амплитуда силы тока в цепи переменного тока частотой 50 Гц, содержащей последовательно соединенные активное сопротивление 1 кОм и конденсатор емкости С = 1 мкФ, если действующее значение напряжения сети, к которой подключен участок цепи, равно 220 В?
Решение
Запишем закон Ома для цепи переменного тока:
I=UZ
Z – полное сопротивление цепи, которое складывается из активного и реактивного сопротивлений.
Z=R2+Xc2Xc=12πϑC
Найдем полное сопротивление, подставив в формулу данные из условия:
X=12·3.14·50·1·10-6=3,18 кОмZ=12·106+3,22·106=3,3 кОм
Далее по действующему значению напряжения найдем амплитудное:
UA=Uд·2=220·2=311 В
Теперь подставим апмлитудное значение напряжения в выражение для закона Ома и вычислим силу тока:
IA=UAZ=3113,3·103=,09 А
Ответ: 0,09 А.
Задача№5. Переменный ток
Условие
Катушка с ничтожно малым активным сопротивлением включена в цепь переменного тока с частотой 50 Гц. При напряжении 125 В сила тока равна 3 А. Какова индуктивность катушки?
Решение
В данной задаче, исходя из условия, можно пренебречь активным сопротивлением катушки. Ее индуктивное сопротивоение равно:
xL=ωL
По закону Ома:
U=IxL=IωL
Отсюда находим индуктивность:
L=UIω=1253·314=,13 Гн
Ответ: 0,13 Гн.
Все еще мало задач? Держите несколько примеров на мощность тока.
Метод векторных диаграмм
Мы уже пользуемся векторными диаграммами, по которым наблюдаем соотношения токов и напряжения в цепях переменного тока. Векторная диаграмма это стоячее изображение вращающихся векторов.
В предыдущих рассуждениях, было сказано, что линейно развернутая диаграмма переменного процесса, (в простом случае синусоидального), точно показывает изменение мгновенного значения переменной величины, то есть происходит все именно так как показывает синусоида и каждая ее точка и есть переменная величина в данный момент. Но оказывается нам интересно не это, нам нужно знать какое значение тока и напряжения и мощности действует в цепи в течение времени, то есть действует длительное время, пока цепь работает.
Анализ синусоид нескольких величин, одновременно действующих в разных фазах, позволяет рассчитать все свойства и режимы работы цепи переменного тока, но гораздо проще это сделать, если отвлечься от синусоид и просто построить соотношение векторов, которые, собственно, и образуют эти синусоиды. Вся информация синусоид заложена в их радиус – векторах. Мы останавливаем эти векторы на рисунке, понимая, что они вращающиеся, но факт их вращения учитываем угловой частотой в расчетных формулах векторной диаграммы.
Итак, векторная диаграмма заменяет линейно развернутую синусоидальную диаграмму, потому, что любая информация, заложенная в синусоиду, есть и в соответствующем ей радиус-векторе.
Если нам приходится рассматривать несколько действующих одновременно синусоидальных процессов, то они изображаются векторной диаграммой, где длина каждого вектора, соответствует действующему значению синусоидальной величины, направление вектора соответствует начальной фазе, синусоидальной величины.
Результирующие значения одновременно действующих напряжений рассчитывается как векторная сумма, где угол между векторами определяется сдвигом фаз между ними.
Расчет цепей переменного тока сводится к расчету треугольников, которые состоят из соответствующих векторов.
Например, можно определить суммарное напряжение, частичные напряжения, и сдвиг фаз между ними.
На основании векторных диаграмм можно построить подобные векторным диаграммам треугольники сопротивлений и треугольники мощностей, решением которых можно определить соотношения сопротивлений, и мощности которые действуют в цепях переменного тока.
Векторная диаграмма напряжений представляет собой векторный треугольник напряжений
Последовательное соединение L R.
Любая катушка наматывается проволокой, а проволока обладает сопротивлением, которое приходится учитывать.
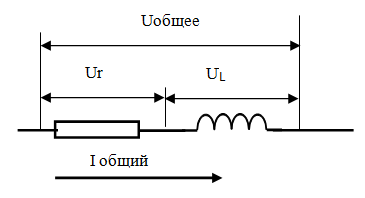
Получается, что реальная цепь, содержащая только L, просто невозможна. В некоторых случаях значением R пренебрегают, и получается, что вроде бы цепь с только L, на самом деле она конечно L R.
Реально, кроме проволоки, в цепи всегда есть и какие – то другие элементы R, поэтому интерес представляют именно цепи L R,
Ток, при последовательном соединении, один и тот же через все сопротивления, а напряжения разные, но общее напряжение не равно просто сумме напряжений на каждом сопротивлении, оно равно векторной сумме, то есть вектор общего напряжения равен сумме векторов напряжений на каждом участке. Для расчетов напряжений надо построить векторную диаграмму.
Векторная диаграмма строится так.
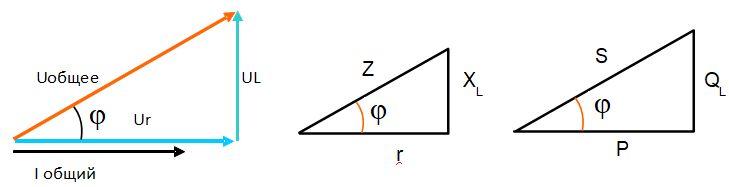
Емкостное сопротивление
Опыт показывает, что если последовательно с лампочкой соединить конденсатор и подключить их к генератору постоянного напряжения, то лампочка не горит. Это понятно, так как обкладки конденсатора разделены диэлектриком, и цепь оказывается разомкнутой. При подключении конденсатора к источнику постоянного тока возникает кратковременный импульс тока, который зарядит конденсатор до напряжения источника, а затем ток прекратится. Но если эту цепь подключить к источнику переменного напряжения, то лампочка горит. Переменный ток представляет собой вынужденные электромагнитные колебания, происходящие под действием переменного электромагнитного поля генератора. При включении конденсатора в цепь переменного тока процесс его зарядки длится четверть периода. После достижения амплитудного значения напряжение между обкладками конденсатора уменьшается, и конденсатор в течение четверти периода разряжается. В следующую четверть периода конденсатор снова заряжается, но знак заряда на его обкладках изменяется на противоположный и т.д. Через диэлектрик, разделяющий обкладки конденсатора, как и в цепи постоянного тока, электрические заряды не проходят. Но по проводам, соединяющим обкладки конденсатора с источником напряжения, течет переменный ток разрядки и зарядки конденсатора. Поэтому лампочка, включенная последовательно с конденсатором, будет гореть непрерывно. Если теперь конденсатор отсоединить, то лампочка горит ярче. Следовательно, конденсатор оказывает переменному току сопротивление, которое называется емкостным сопротивлением.
Рассмотрим цепь (рис. 1), состоящую из конденсатора и подводящих проводов, сопротивление которых пренебрежительно мало, и генератора переменного напряжения.
Рис. 1
Пусть напряжение на конденсаторе изменяется по закону \(~U = U_0\sin wt.\) Как известно, заряд на обкладках конденсатора можно определить по формуле \(~q = CU = CU_0\sin wt.\) Сила тока \(~I = q’.\) Следовательно,
\(~I = -wCU_0\cos wt = wCU_0\sin(wt+\frac {\pi}2).\)
Отсюда \(~I=I_0\sin (wt +\frac {\pi}2),\)
где \(~I_0=wCU_o\) — амплитудное значение силы тока:
\(~I_0=\frac {U_0}{\frac 1{wC}}; I_0 =\frac {U_0}{X_C},\)
где \(~X_C = \frac 1{wC}.\)
Выразив амплитудные значения через действующие \(~I_0 = \sqrt2 I \) и \(~U_0 = \sqrt2 U,\) получим \(~I= \frac U{X_C}, \) т.е. действующее значение силы тока связано с деиству-Хс ющим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение на участке цепи постоянного тока. Это позволяет рассматривать величину Хс как сопротивление конденсатора переменному току:
\(~X_C = \frac 1{wC}\) — емкостное сопротивление.
В СИ единицей емкостного сопротивления является ом (Ом).
Как видно из полученной выше формулы, если в цепи включено только емкостное сопротивление, колебания силы тока в этой цепи опережают по фазе колебания напряжения на конденсаторе на \(~\frac {\pi}2,\) что изображено на графике и на векторной диаграмме (рис. 2).
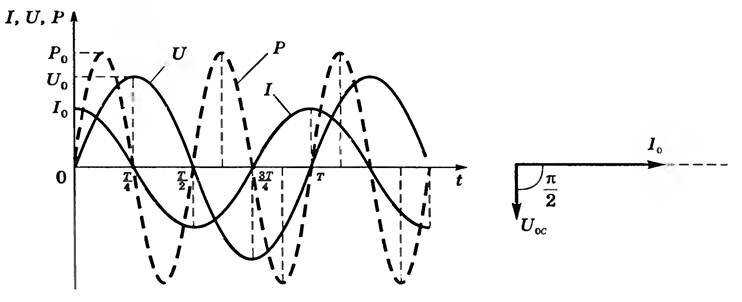
Рис. 2
Мгновенная мощность
\(~P=IU = I_0\sin (wt +\frac {\pi}2)U_0\sin wt = I_0U_0\sin wt \cos wt =\frac {I_0U_0}2 \sin 2wt,\)
т.е. мощность периодически изменяется с двойной частотой, а среднее значение мощности — за период \(\mathcal h P \mathcal i =0,\) так как \(~\mathcal h \sin 2wt \mathcal i = 0.\) Первую и третью четверти периода, когда конденсатор заряжается, он получает энергию от генератора, а вторую и четвертую четверти периода, когда конденсатор разряжается, он отдает энергию генератору.
Таким образом, так же, как активное сопротивление, емкостное сопротивление ограничивает силу тока в цепи, но в отличие от активного сопротивления на емкостном сопротивлении электрическая энергия не превращается необратимо в другие виды энергии.
§ 66. Цепь переменного тока, содержащая емкость
Если в цепь постоянного тока включить конденсатор (идеальный — без потерь), то в течение очень короткого времени после включения по цепи потечет зарядный ток. После того как конденсатор зарядится до напряжения, равного напряжению источника, кратковременный ток в цепи прекратится. Следовательно, для постоянного тока конденсатор представляет собой разрыв цепи, или, иными словами, бесконечно большое сопротивление.
Если же конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном, то в другом направлении.
При этом в цепи будет проходить переменный ток. Рассмотрим это явление подробнее.
В момент включения напряжение на конденсаторе равно нулю. В течение первой четверти периода, когда напряжение сети будет возрастать (рис. 143), конденсатор будет заряжаться.
Рис. 143. Графики и векторная диаграмма для цепи переменного тока, содержащей емкость
По мере накопления зарядов на обкладках конденсатора напряжение конденсатора увеличивается. Когда напряжение сети к концу первой четверти периода достигнет максимального значения Um, напряжение конденсатора также станет равным Um, заряд конденсатора прекращается и ток в цепи становится равным нулю.
Ток в цепи конденсатора можно определить по формуле
i = Δq/Δt,
где Δq — количество электричества, протекающее по цепи за время Δt.
Из электростатики известно:
q = CuC = Cu,
где С — емкость конденсатора;
u — напряжение сети;
uС — напряжение конденсатора.
Окончательно для тока имеем
i = C ΔuC/Δt = C Δu/Δt.
Из последнего выражения видно, что, когда Δu/Δt максимально (положения а, в, д), i также максимально.
Когда Δu/Δt = 0 (положения б, г на рис. 143), то i также равно нулю.
Во вторую четверть периода напряжение сети будет уменьшаться, и конденсатор начнет разряжаться. Ток в цепи меняет свое направление на обратное.
В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд.
Из рис. 143 видно, что ток I в цепи с емкостью в своих изменениях опережает по фазе напряжение конденсатора на 1/4 периода, или 90°.
Сравнивая векторные диаграммы цепей с индуктивностью и емкостью, мы видим, что индуктивность и емкость на фазу тока влияют прямо противоположно.
Пользуясь высшей математикой, можно доказать, что ток в цепи с емкостью пропорционален напряжению UС, приложенному к конденсатору, угловой частоте со и величине емкости конденсатора С;
I = UСωС = 2πfСUС.
Обозначим
xC = 1/2πfC = 1/ωC.
Величина xС называется емкостным сопротивлением, или реактивным сопротивлением емкости, и измеряется в омах. Выражение закона Ома для цепи переменного тока, содержащей емкость, имеет вид
I = U/xC.
Та часть напряжения сети, которая приложена к конденсатору, называется емкостным падением напряжения (или реактивной слагающей напряжения) и обозначается UC:
UC = I ⋅ xC.
Емкостное сопротивление хС, так же как индуктивное сопротивление xL, зависит от частоты переменного тока.
Но если с увеличением частоты индуктивное сопротивление увеличивается, то емкостное сопротивление, наоборот, будет уменьшаться.
Пример 6. Определить сопротивление конденсатора емкостью 5 мкф при частоте 50 гц:
xС = 1/2πfС = 1/2⋅3,14⋅50⋅5⋅10-6 = 636 ом,
при частоте 400 гц:
xС = 1/2⋅3,14⋅400⋅5⋅10-6 = 79,5 ом.
На рис. 144 показана кривая мгновенной мощности в цепи с емкостью. Из чертежа видно, что в первую четверть периода цепь с емкостью забирает из сети энергию, которая запасается в электрическом поле конденсатора.
Рис. 144. Кривая мгновенной мощности в цепи с емкостью
Энергию, запасаемую конденсатором к моменту, когда напряжение на нем равно максимальному значению, можно определить по известной формуле CUм2/2.
В следующую четверть периода конденсатор разряжается на сеть, отдавая ей ранее запасенную в нем энергию.
За вторую половину периода явление колебаний энергии повторяется. Таким образом, в цепи с емкостью происходит лишь обмен энергией между сетью и конденсатором без ее потерь.
Поэтому средняя за период мощность, или активная мощность, цепи с емкостью равна нулю, как и в цепи с индуктивностью.
Из графика, изображенного на рис. 144, видно, что мгновенная мощность в цепи с емкостью два раза в течение каждого периода (когда ωt = 45°, 135° и т. д.) достигает максимального значения, равного Uм/√2 ⋅ Iм/√2 = UI.
Этой величиной принято характеризовать количественно процесс обмена энергии между источником и электрическим полем конденсатора. Ее также называют реактивной мощностью и обозначают буквой Q.
Учитывая, что в рассматриваемой цепи U = IxC, получим следующее выражение для реактивной мощности:
Q = I2xC.
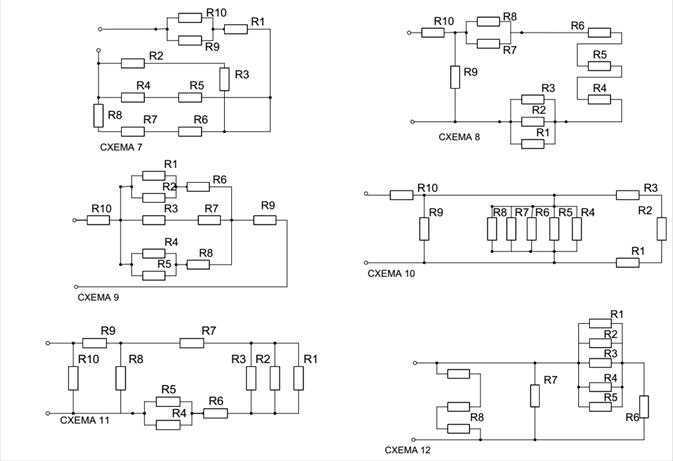
ЗАДАЧА №1. Расчёт простых цепей постоянного тока со смешанным соединением
Задана электрическая цепь постоянного тока смешанного соединения,состоящая из 10 резисторов. Значения сопротивления резисторов и номер схемы для соответствующего варианта указаны в таблице №1.
Определить: эквивалентное сопротивление участка цепи Rэкв ; мощность P, напряжение U, силу тока I на входе цепи; токи Ii и напряжения Ui на всех элементах цепи. В ходе решения выполнить несколько проверок полученных результатов по законам Кирхгофа.
Таблица №1
| №
варианта |
№
схемы |
P | U | I | R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | R10 |
| Вт | В | А | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом | ||
| 1 | 1 | ? | 150 | ? | 6 | 3 | 8 | 12 | 15 | 12 | 2 | 10 | 15 | 5 |
| 2 | 2 | ? | 300 | ? | 10 | 40 | 2 | 10 | 20 | 15 | 60 | 7 | 15 | 30 |
| 3 | 3 | ? | 240 | ? | 20 | 30 | 60 | 20 | 20 | 5 | 25 | 50 | 8 | 36 |
| 4 | 4 | ? | 360 | ? | 2 | 5 | 3 | 20 | 60 | 30 | 7 | 15 | 60 | 6 |
| 5 | 5 | ? | 200 | ? | 2 | 13 | 30 | 10 | 20 | 4 | 8 | 3 | 6,5 | 60 |
| 6 | 6 | ? | 300 | ? | 10 | 20 | 60 | 4 | 5 | 15 | 45 | 6 | 2 | 3 |
| 7 | 7 | ? | 500 | ? | 3 | 15 | 15 | 8 | 7 | 10 | 10 | 10 | 30 | 20 |
| 8 | 8 | ? | 300 | ? | 20 | 5 | 4 | 8 | 7 | 3 | 15 | 30 | 6 | 10 |
| 9 | 9 | ? | 600 | ? | 15 | 30 | 15 | 10 | 40 | 10 | 45 | 2 | 9 | 5 |
| 10 | 10 | ? | 300 | ? | 0,2 | 0,8 | 2 | 4 | 5 | 6 | 30 | 60 | 2 | 15 |
| 11 | 11 | ? | 360 | ? | 60 | 12 | 15 | 30 | 15 | 3 | 1 | 60 | 5 | 30 |
| 12 | 12 | ? | 150 | ? | 5 | 8 | 10 | 20 | 40 | 23 | 25 | 5 | 15 | 35 |
| 13 | 1 | ? | ? | 40 | 15 | 30 | 20 | 30 | 20 | 12 | 10 | 5 | 10 | 60 |
| 14 | 2 | ? | ? | 40 | 3 | 6 | 8 | 10 | 20 | 15 | 60 | 17 | 10 | 60 |
| 15 | 3 | ? | ? | 20 | 10 | 20 | 60 | 15 | 30 | 4 | 30 | 60 | 2 | 60 |
| 16 | 4 | ? | ? | 18 | 15 | 5 | 40 | 10 | 20 | 30 | 10 | 15 | 30 | 4 |
| 17 | 5 | ? | ? | 100 | 10 | 10 | 20 | 5 | 8 | 8 | 20 | 1 | 1 | 6 |
| 18 | 6 | ? | ? | 100 | 6 | 24 | 8 | 40 | 20 | 20 | 10 | 7,5 | 15 | 7,5 |
| 19 | 7 | ? | ? | 50 | 5 | 15 | 15 | 7 | 8 | 5 | 10 | 15 | 6 | 3 |
| 20 | 8 | ? | ? | 20 | 20 | 4 | 5 | 1 | 3 | 5 | 30 | 15 | 14 | 6,6 |
| 21 | 9 | ? | ? | 20 | 6 | 3 | 8 | 9 | 4,5 | 10 | 7 | 7 | 4 | 4 |
| 22 | 10 | ? | ? | 30 | 1 | 2 | 3 | 4 | 5 | 30 | 60 | 3 | 2 | 4/3 |
| 23 | 11 | ? | ? | 20 | 6 | 8 | 24 | 6 | 3 | 4 | 5 | 30 | 10 | 60 |
| 24 | 12 | ? | ? | 80 | 1 | 2 | 3 | 12 | 12 | 0,5 | 5 | 6 | 7 | 2 |
| 25 | 1 | ? | ? | 20 | 10 | 15 | 14 | 12 | 15 | 20 | 4 | 7 | 15 | 30 |
| 26 | 2 | 1620 | ? | ? | 6 | 3 | 3 | 2 | 5 | 30 | 15 | 14 | 20 | 12 |
| 27 | 3 | 2000 | ? | ? | 60 | 10 | 20 | 40 | 10 | 1 | 20 | 12 | 5 | 10 |
| 28 | 4 | ? | ? | 30 | 5 | 10 | 15 | 15 | 30 | 15 | 10 | 20 | 12 | 3 |
| 29 | 5 | 3200 | ? | ? | 20 | 15 | 10 | 12 | 15 | 20 | 30 | 2 | 5 | 40 |
| 30 | 6 | ? | 280 | ? | 20 | 4 | 5 | 20 | 40 | 20 | 10 | 12 | 4 | 6 |
| 31 | 7 | 50000 | ? | ? | 22 | 2 | 8 | 5 | 15 | 10 | 20 | 30 | 10 | 40 |
| 32 | 8 | 1440 | ? | ? | 20 | 60 | 10 | 0,4 | 0,6 | 1 | 15 | 30 | 9 | 4 |
| 33 | 9 | ? | ? | 40 | 15 | 30 | 15 | 10 | 40 | 10 | 45 | 2 | 9 | 5 |
| 34 | 10 | 2250 | ? | ? | 2 | 3 | 10 | 10 | 12 | 15 | 20 | 30 | 10 | 8 |
| 35 | 11 | ? | ? | 16 | 60 | 12 | 15 | 30 | 15 | 3 | 1 | 60 | 5 | 30 |
| 36 | 12 | 1280 | ? | ? | 5 | 8 | 10 | 20 | 40 | 10 | 15 | 8 | 10 | 12 |
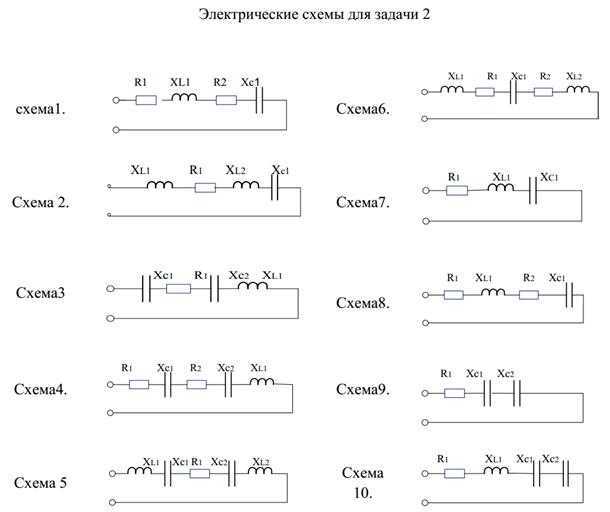
ЗАДАЧА №2. Однофазные цепи переменного тока.
Неразветвлённая цепь переменного тока, показанная на соответствующем рисунке, содержит активные и реактивные сопротивления, величны которых заданы в таблице №2. Кроме того извесен один из дополнительных параметров. Определить следующие величины, если они не заданы в таблице параметов.
1. полное сопротивление цепи Z;
2. напряжение, приложенное к цепи U;
3. силу тока в цепи I;
4. сдвиг фаз φ;
5. активную P, реактивную Q и полную S мощности, потребляемые цепью;
6. начертить в масштабе векторную диаграмму и пояснить ее построение.
Таблица №2
| №
варианта |
№
схемы |
R1 | R2 | Дополнительный параметр | ||||
| Ом | Ом | Ом | Ом | Ом | Ом | |||
| 1 | 1 | 8 | 4 | 18 | — | 2 | — | I = 10 A |
| 2 | 2 | 16 | — | 5 | 6 | 8 | — | Q= 135 ВАР |
| 3 | 3 | 4 | — | 9 | — | 3 | 3 | U = 20 B |
| 4 | 4 | 10 | 14 | 18 | — | 20 | 30 | UR2 = 28 B |
| 5 | 5 | 32 | — | 20 | 20 | 6 | 10 | I = 4 A |
| 6 | 6 | 4 | — | 5 | 6 | 3 | — | I = 5 A |
| 7 | 7 | 8 | — | 12 | — | — | 6 | P = 72 Вт |
| 8 | 8 | 2 | 6 | — | 10 | 4 | — | U = 20 B |
| 9 | 9 | 3 | — | — | — | 1 | 4 | Q= 125 ВАР |
| 10 | 10 | 8 | — | — | — | 4 | 2 | U = 80 B |
| 11 | 1 | 1 | 2 | 8 | — | 4 | — | S = 1000 ВА |
| 12 | 2 | 3 | — | 10 | 12 | 26 | — | P1 = 48 Вт |
| 13 | 10 | 12 | — | 22 | — | 2 | 4 | P = 72 Вт |
| 14 | 3 | 40 | — | 50 | — | 12 | 8 | QL1 = 48 ВАР |
| 15 | 4 | 40 | 20 | 20 | — | 80 | 20 | QC1 = — 320 ВАР |
| 16 | 5 | 32 | — | 25 | 15 | 8 | 8 | UL1 = 125 B |
| 17 | 6 | 8 | — | 10 | 15 | 9 | — | QC1 = — 320 ВАР |
| 18 | 7 | 4 | — | 5 | — | — | 9 | P = 256 Вт |
| 19 | 8 | 10 | 6 | — | 20 | 8 | — | I = 4 A |
| 20 | 9 | 8 | — | — | — | 4 | 2 | S = 50 ВА |
| 21 | 10 | 4 | — | 10 | — | 3 | 4 | P = 64 Вт |
| 22 | 1 | 8 | 4 | 6 | — | 22 | — | P1 = 32 Вт |
| 23 | 2 | 4 | — | 3 | 6 | 12 | — | S = 500 ВА |
| 24 | 3 | 12 | — | 16 | — | 10 | 6 | UL2 = 160 В |
| 25 | 4 | 6 | 2 | 10 | — | 1 | 3 | P = 200 Вт |
| 26 | 5 | 80 | — | 10 | 10 | 40 | 40 | QL2 = 40 ВАР |
| 27 | 6 | 4 | — | 10 | 15 | 9 | — | Q= 1600 ВАР |
| 28 | 7 | 4 | — | 5 | — | — | 8 | Q= -192 ВАР |
| 29 | 8 | 6 | 2 | — | 4 | 10 | — | Q= -24 ВАР |
| 30 | 9 | 16 | — | — | — | 8 | 4 | P = 64 Вт |
| 31 | 10 | 12 | — | 4 | — | 12 | 8 | U = 100 B |
| 32 | 1 | 2 | 2 | 4 | — | 8 | — | Q1 = -96 ВАР |
| 33 | 2 | 8 | — | 2 | 2 | 10 | — | QC1 = — 20 ВАР |
| 34 | 3 | 24 | — | 28 | — | 35 | 25 | S = 1000 ВА |
| 35 | 4 | 30 | 34 | 32 | — | 50 | 30 | UC1 = 500 В |
| 36 | 5 | 40 | — | 10 | 10 | 20 | 20 | QL2 = 20 ВАР |
ЗАДАЧА №3. Трехфазные цепи переменного тока.
Три группы сопротивлений соединили «звездой» с нулевым проводом и включили в трехфазную сеть переменного тока с линейным напряжением Uл ном. Активные сопротивления в фазах А, В и С соответственно равны RA, RB, RC; реактивные – XA, XB, Xc. Характер реактивных сопротивлений указан на схеме цепи (индуктивное или ёмкостное). Линейные токи в нормальном режиме равны IA, IB, IC. Фазы нагрузки потребляют активные мощности PA, PB, PC и реактивные мощности QA, QB, QC. Начертить схему цепи для каждого варианта. Определить величины, отмеченные в таблице №3 прочерками. Начертить в масштабе векторную диаграмму цепи. Из векторной диаграммы определить ток в нулевом проводе.
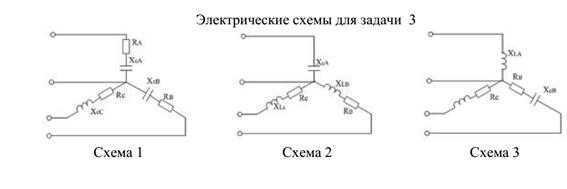
Таблица №3
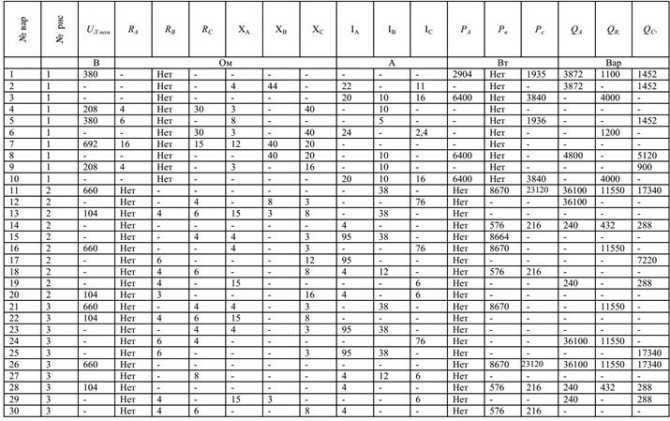
Пример расчёта
Ёмкостное и индуктивное сопротивления относятся к реактивным, то есть таким, которые не потребляют мощности. Поэтому закон Ома для участка схемы с ёмкостью имеет вид I = U/Xc, где ток и напряжение обозначают действующие значения. Именно из-за этого конденсаторы используются в цепях для разделения не только постоянных и переменных токов, но и низкой и высокой частот. При этом чем ёмкость будет ниже, тем более высокой частоты сможет пройти ток. Если же последовательно с конденсатором включено активное сопротивление, то общий импеданс цепи находится как Z = (R 2 +Xc 2 ) ½.
Практическое применение формул можно рассмотреть при решении задачи. Пусть имеется RC цепочка, состоящая из ёмкости C = 1 мкФ и сопротивления R = 5 кОм. Необходимо найти импеданс этого участка и ток цепи, если частота сигнала равна f = 50 Гц, а амплитуда U = 50 В.
В первую очередь понадобится определить сопротивление конденсатора в цепи переменного тока для заданной частоты. Подставив данные в формулу, получим, что для частоты 50 Гц сопротивление будет
Xc = 1/ (2*p*F*C) = 1/ (2*3,14*50*1* 10 −6 ) = 3,2 кОм.
По закону Ома можно найти ток: I = U /Xc = 50 /3200 = 15,7 мА.
Напряжение берётся изменяемым по закону синуса, поэтому: U (t) = U * sin (2*p*f*t) = 50*sin (314*t). Соответственно, ток будет I (t) = 15,7* 10 −3 + sin (314*t+p/2). Используя полученные результаты, можно построить график тока и напряжения при этой частоте. Общее сопротивление участка цепи находим как Z = (50002+32002)½ = 5 936 Ом =5,9 кОм.
Таким образом, подсчитать полное сопротивление на любом участке цепи несложно. При этом можно воспользоваться и так называемыми онлайн-калькуляторами, куда вводят начальные данные, такие как частота и ёмкость, а все расчёты выполняются автоматически. Это удобно, так как нет необходимости запоминать формулы и вероятность ошибки при этом стремится к нулю.































