Емкостное сопротивление конденсатора: влияние на переменный и постоянный ток, формулы для расчета

Лабораторные работы по разделу Электричество

1. Краткое теоретическое описание

В цепи переменного тока кроме резисторов могут использоваться катушки индуктивности и конденсаторы. Для постоянного тока катушка индуктивности имеет только активное сопротивление, которое обычно невелико (если катушка не содержит большое количество витков). Конденсатор же в цепи постоянного тока представляет «разрыв» (очень большое активное сопротивление). Для переменного тока эти элементы обладают специфическим реактивным сопротивлением, которое зависит как от номиналов деталей, так и от частоты переменного тока, протекающего через катушку и конденсатор.

1.1. Катушка в цепи переменного тока.

Рассмотрим, что происходит в цепи, содержащей резистор и катушку индуктивности. Колебания силы тока, протекающего через катушку:

Основы электротехники выполнение курсовой работы Преобразовать соединение звездой сопротивлений в эквивалентное соединение треугольником сопротивлений

вызывают падение напряжения на концах катушки в соответствии с законом самоиндукции и правилом Ленца:

т.е. колебания напряжения опережают по фазе колебания силы тока на p /2. Произведение w LIm

является амплитудой колебания напряжения:

Произведение циклической частоты на индуктивность называют индуктивным сопротивлением

катушки:

(1)

поэтому связь между амплитудами напряжения и тока на катушке совпадает по форме с законом Ома для участка цепи постоянного тока:

(2)

Как видно из выражения (1), индуктивное сопротивление не является постоянной величиной для данной катушки, а пропорционально частоте переменного тока через катушку. Поэтому амплитуда колебаний силы тока Im

в проводнике с индуктивностьюL при постоянной амплитудеUL напряжения убывает обратно пропорционально частоте переменного тока:

1.2. Конденсатор в цепи переменного тока.

При изменении напряжения на обкладках конденсатора по гармоническому закону:

заряд q

на его обкладках изменяется также по гармоническому закону:

Электрический ток в цепи возникает в результате изменения заряда конденсатора, поэтому колебания силы тока в цепи будут происходить по закону:

Видно, что колебания напряжения на конденсаторе отстают по фазе от колебаний силы тока на p /2. Произведение w CUm

является амплитудой колебаний силы тока:

Аналогично тому, как было сделано с индуктивностью, введем понятие емкостного сопротивления

конденсатора:

(3)

Для конденсатора получаем соотношение, аналогичное закону Ома:

(4)

Формулы (2) и (4) справедливы и для эффективных значений тока и напряжения.

Порядок выполнения работы
Соберите цепь показанную на рисунке 1.
Установите следующие значения параметров:

Генератор – напряжение (эффективное) 100 В, частота 100 Гц;

Конденсатор – рабочее напряжение 400 В, емкость 10 мкФ;

Резистор – рабочая мощность 500 Вт, сопротивление 100 Ом.

Изменяя емкость конденсатора от 5 до 50 мкФ (через 5 мкФ), запишите показания вольтметров (напряжение на конденсаторе и на резисторе).
Рассчитайте эффективное значение токов, текущих в цепи, в зависимости от значения емкости конденсатора (для этого надо напряжение на резисторе разделить на его сопротивление).
Определите значения емкостных сопротивлений конденсатора для соответствующих значений его емкости и сравните их с рассчитанными по формуле (3).
Установите емкость конденсатора 10 мкФ. Изменяя частоту генератора от 20 до 100 Гц через 10 Гц, повторите измерения и расчеты емкостного сопротивления в зависимости от частоты переменного тока.
Соберите цепь показанную на рисунке 2.

Рис.1. Рис.2.

Установите следующие значения параметров:

Генератор – напряжение (эффективное) 100 В, частота 100 Гц;

Катушка — индуктивность 50 мГн;

Резистор – рабочая мощность 500 Вт, сопротивление 100 Ом.

Изменяя индуктивность катушки от 50 до 500 мГн (через 50 мГн), запишите показания вольтметров (напряжение на катушке и на резисторе).
Рассчитайте эффективное значение токов, текущих в цепи, в зависимости от значения индуктивности катушки (для этого надо напряжение на резисторе разделить на его сопротивление).
Определите индуктивные сопротивления катушки для соответствующих значений ее индуктивности и сравните их с рассчитанными по формуле (1).
Установите индуктивность катушки 100 мГн. Изменяя частоту генератора от 20 до 100 Гц через 10 Гц, повторите измерения и расчеты индуктивного сопротивления в зависимости от частоты переменного тока..
Постройте графики зависимостей индуктивного и емкостного сопротивлений от частоты переменного тока.

Емкостной элемент в цепи постоянного тока

Протекание тока в электрической цепи, содержащей индуктивность, сопровождается возникновением магнитного поля в окружающей среде. Магнитному полю присуща энергия, равная работе, совершаемой электрическим током I в процессе создания поля и численно равная W = LI ² /2.

В электрической цепи, содержащей емкостной элемент, электрические заряды могут не только перемещаться по ее элементам, но также накапливаться в них, создавая запас энергии W = CU ² /2.

Наиболее часто емкостные и индуктивные элементы применяются в электрических схемах в качестве всевозможных частотных фильтров и колебательных контуров.

Источник

Закон Ома для постоянного тока — расчет, формулы

Закон Ома для постоянного тока определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи.

Закон Ома для полной цепи:

I = ε / (R + r), где:

• ε — ЭДС источника напряжения, В;
• I — сила тока в цепи, А;
• R — сопротивление всех внешних элементов цепи, Ом;
• r — внутреннее сопротивление источника напряжения, Ом.

Из закона Ома для полной цепи вытекают следующие следствия:

• При r < R сила тока в цепи обратно пропорциональна ее сопротивлению, а сам источник в ряде случаев может быть назван источником напряжения.
• При r > R сила тока не зависит от свойств внешней цепи (величины нагрузки), и источник может быть назван источником тока.

Часто выражение I = U / R тоже называют законом Ома. При этом формулировка следующая — сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, где:

• I — сила тока, измеряемая в Амперах (A).
• U — напряжение, измеряемое в Вольтах (V).
• R — сопротивление, измеряемое в Омах (Ом, Ω).

Помимо закона Ома, важнейшим является понятие электрической мощности. Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U):

P = I × U, где:

• P — электрическая мощность, измеряемая в Ваттах (W).
• I — сила тока, измеряемая в Амперах (A).
• U — напряжение, измеряемое в Вольтах (V).

Комбинируя две формулы можно получить зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:

Множительные приставки в системе СИ примирительные к закону Ома:

• Сила тока, Амперы (A): 1 килоампер (1 kА) = 1000 А; 1 миллиампер (1 mA) = 0,001 A; 1 микроампер (1 µA) = 0,000001 A.
• Напряжение, Вольты (V): 1 киловольт (1kV) = 1000 V; 1 милливольт (1 mV) = 0,001 V; 1 микровольт (1 µV) = 0,000001 V.
• Сопротивление, Омы (Ом): 1 мегаом (1 MОм) = 1000000 Ом; 1 килоом (1 kОм) = 1000 Ом.
• Мощность, Ватты (W): 1 мегаватт (1 MW) = 1000000 W; 1 киловатт (1 kW) = 1000 W; 1 милливатт (1 mW) = 0,001 W.

Импеданс элемента

Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе. Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние.

Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.

Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где

• Xl — индуктивность;
• Xс — ёмкость;
• R — активная составляющая.

Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.

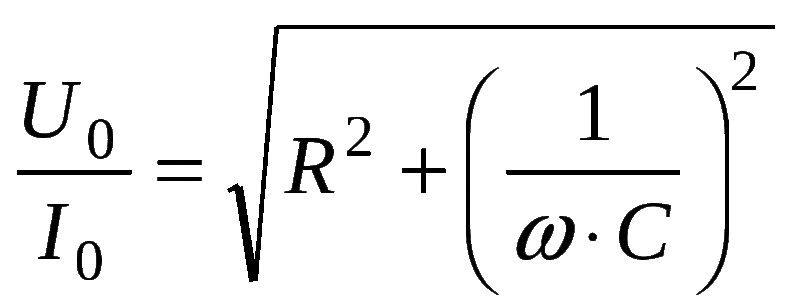
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:

• X > 0, в элементе проявляются индуктивные свойства;
• X = 0, в ёмкости присутствует только активная величина;
• X < 0, в элементе проявляется ёмкостное сопротивление.

Ёмкостное сопротивление

Для понимания процесса следует представить конденсатор в электрической цепи, по которой течёт переменный ток. Причём в этой цепи нет других элементов. Значение тока, проходящего через конденсатор, и напряжения, приложенного к его обкладкам, изменяется по времени. Зная любое из этих значений, можно найти другое.

Пускай ток изменяется по синусоидальной зависимости I (t) = Im * sin (w*t+ f 0). Тогда напряжение можно описать как U (t) = (Im/C*w) *sin (w*t+ f 0 -p/2). При учёте в формуле сдвига фаз на 90 градусов, возникающего между сигналами, вводится комплексная величина j, называемая мнимой единицей. Поэтому формула для нахождения тока будет выглядеть как I = U /(1/j*w*C). Но учитывая, что комплексное число только обозначает смещение напряжения относительно тока, а на их амплитудные значения не влияет, его можно убрать из формулы, тем самым значительно её упростив.

Так как по закону Ома сопротивление прямо пропорционально напряжению на участке цепи и обратно пропорционально току, то преобразуя формулы, можно будет получить следующее выражение:

Xc = 1/w*C = ½*p*f*C. Единица измерения — ом.

Становится понятно, что ёмкостное сопротивление зависит не только от ёмкости, но и от частоты. При этом чем больше эта частота, тем меньшее сопротивление конденсатор будет оказывать проходимому через него току. По отношению к ёмкости это утверждение будет обратным. Вот поэтому для постоянного тока, частота которого равна нулю, сопротивление накопителя будет бесконечно большим.

На практике всё немного по-другому. Чем ближе частота сигнала приближается к нулевому значению, тем больше становится сопротивление конденсатора, но при этом разрыв цепи наступить всё равно не может. Связанно это с током утечки. В случае когда частота стремится к бесконечности, сопротивление конденсатора должно становиться нулевым, но этого тоже не происходит — из-за присутствия паразитной индуктивности и всё того же тока утечки.

Индуктивная составляющая

При прохождении переменного сигнала через накопитель, его можно представить в виде последовательно включённой с источником питания катушки индуктивности. Эта катушка характеризуется большим сопротивлением в цепи переменного сигнала, чем постоянного. Значение силы тока в определённой точке времени находится как I = I 0 * sinw .

Приняв во внимание, что мгновенная величина напряжения U 0 обратна по знаку мгновенному значению ЭДС самоиндукции E 0, а также используя правило Ленца, можно получить выражение E = L * I, где L — индуктивность

Следовательно: U = L*w * I 0 *cosw*t = U 0 *sin (wt + p /2) , причём ток отстаёт от напряжения на p /2. Используя закон Ома и приняв, что сопротивление катушки равно w * L, получится формула для участка электрической цепи, имеющая только индуктивную составляющую: U 0 = I 0 / w * L.

Характеристики прибора

Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:

C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними.

Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:

• удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
• рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
• температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
• сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
• эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
• абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
• ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
• полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
• эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.

§ 66. Цепь переменного тока, содержащая емкость

Если в цепь постоянного тока включить конденсатор (идеальный — без потерь), то в течение очень короткого времени после включения по цепи потечет зарядный ток. После того как конденсатор зарядится до напряжения, равного напряжению источника, кратковременный ток в цепи прекратится. Следовательно, для постоянного тока конденсатор представляет собой разрыв цепи, или, иными словами, бесконечно большое сопротивление.

Если же конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном, то в другом направлении.

При этом в цепи будет проходить переменный ток. Рассмотрим это явление подробнее.

В момент включения напряжение на конденсаторе равно нулю. В течение первой четверти периода, когда напряжение сети будет возрастать (рис. 143), конденсатор будет заряжаться.

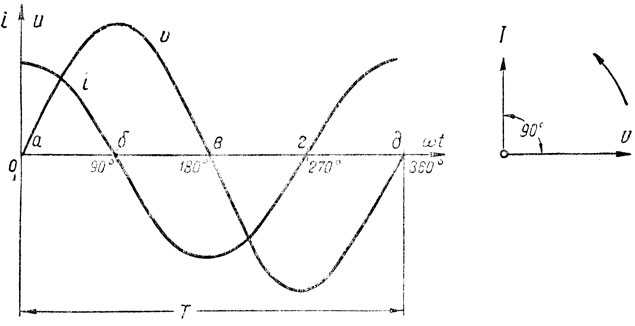Рис. 143. Графики и векторная диаграмма для цепи переменного тока, содержащей емкость

По мере накопления зарядов на обкладках конденсатора напряжение конденсатора увеличивается. Когда напряжение сети к концу первой четверти периода достигнет максимального значения U_m, напряжение конденсатора также станет равным U_m, заряд конденсатора прекращается и ток в цепи становится равным нулю.

Ток в цепи конденсатора можно определить по формуле

i = Δq/_Δt,

где Δq — количество электричества, протекающее по цепи за время Δt.

Из электростатики известно:

q = Cu_C = Cu,

где С — емкость конденсатора;

u — напряжение сети;

u_С — напряжение конденсатора.

Окончательно для тока имеем

i = C Δu_C/_Δt = C Δu/_Δt.

Из последнего выражения видно, что, когда Δu/_Δt максимально (положения а, в, д), i также максимально.

Когда Δu/_Δt = 0 (положения б, г на рис. 143), то i также равно нулю.

Во вторую четверть периода напряжение сети будет уменьшаться, и конденсатор начнет разряжаться. Ток в цепи меняет свое направление на обратное.

В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд.

Из рис. 143 видно, что ток I в цепи с емкостью в своих изменениях опережает по фазе напряжение конденсатора на 1/4 периода, или 90°.

Сравнивая векторные диаграммы цепей с индуктивностью и емкостью, мы видим, что индуктивность и емкость на фазу тока влияют прямо противоположно.

Пользуясь высшей математикой, можно доказать, что ток в цепи с емкостью пропорционален напряжению U_С, приложенному к конденсатору, угловой частоте со и величине емкости конденсатора С;

I = U_СωС = 2πfСU_С.

Обозначим

x_C = 1/_2πfC = 1/_ωC.

Величина x_С называется емкостным сопротивлением, или реактивным сопротивлением емкости, и измеряется в омах. Выражение закона Ома для цепи переменного тока, содержащей емкость, имеет вид

I = U/_xC.

Та часть напряжения сети, которая приложена к конденсатору, называется емкостным падением напряжения (или реактивной слагающей напряжения) и обозначается U_C:

U_C = I ⋅ x_C.

Емкостное сопротивление х_С, так же как индуктивное сопротивление x_L, зависит от частоты переменного тока.

Но если с увеличением частоты индуктивное сопротивление увеличивается, то емкостное сопротивление, наоборот, будет уменьшаться.

Пример 6. Определить сопротивление конденсатора емкостью 5 мкф при частоте 50 гц:

x_С = 1/_2πfС = 1/_{2⋅3,14⋅50⋅5⋅10-6} = 636 ом,

при частоте 400 гц:

x_С = 1/_{2⋅3,14⋅400⋅5⋅10-6} = 79,5 ом.

На рис. 144 показана кривая мгновенной мощности в цепи с емкостью. Из чертежа видно, что в первую четверть периода цепь с емкостью забирает из сети энергию, которая запасается в электрическом поле конденсатора.

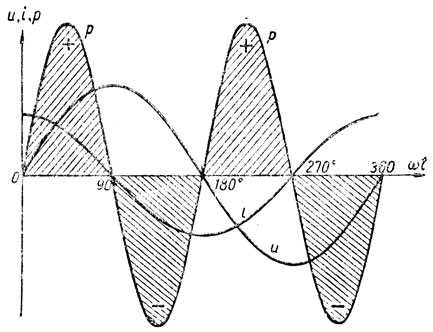Рис. 144. Кривая мгновенной мощности в цепи с емкостью

Энергию, запасаемую конденсатором к моменту, когда напряжение на нем равно максимальному значению, можно определить по известной формуле CU_м2/₂.

В следующую четверть периода конденсатор разряжается на сеть, отдавая ей ранее запасенную в нем энергию.

За вторую половину периода явление колебаний энергии повторяется. Таким образом, в цепи с емкостью происходит лишь обмен энергией между сетью и конденсатором без ее потерь.

Поэтому средняя за период мощность, или активная мощность, цепи с емкостью равна нулю, как и в цепи с индуктивностью.

Из графика, изображенного на рис. 144, видно, что мгновенная мощность в цепи с емкостью два раза в течение каждого периода (когда ωt = 45°, 135° и т. д.) достигает максимального значения, равного U_м/_√2 ⋅ I_м/_√2 = UI.

Этой величиной принято характеризовать количественно процесс обмена энергии между источником и электрическим полем конденсатора. Ее также называют реактивной мощностью и обозначают буквой Q.

Учитывая, что в рассматриваемой цепи U = Ix_C, получим следующее выражение для реактивной мощности:

Q = I2x_C.

Свойства емкостей

Общее сопротивление

При параллельном включении нескольких конденсаторов их ёмкости складываются между собой. При этом общее ёмкостное сопротивление (согласно рассмотренным выше формулам) уменьшается. Если же все конденсаторные элементы соединены в последовательную цепочку, их суммарная ёмкость вычисляется как обратные значения каждой из составляющей.

Ёмкостное сопротивление последовательно включенных элементов в этом случае, наоборот, увеличивается. В заключение отметим, что такой характер изменения ёмкости и импеданса объясняется свойствами конденсатора, способного накапливать заряд на своих обкладках.

Что такое конденсатор

Конденсаторы — это пассивные элементы, используемые при формировании разнообразных электротехнических схем, блокирующих и защитных устройств. Будучи включённым в переменную цепь накопитель аккумулирует и возвращает энергию. Если подключается переменный, то энергия возвращается в систему, при этом поддерживается периодичность, которая соответствует рабочей частоте.

Что собой представляют конденсаторы

К сведению! Когда через конденсатор протекает переменный ток, то он непрерывно оказывает ему сопротивление, величина которого обратно пропорционально зависит от частоты.

Уменьшение частоты приводит к повышению сопротивления. Когда источник, генерирующий такой ток, подключается к накопителю, то максимальное напряжение определяется силой.

Чтобы на примере убедиться в возможности проведения переменного тока, формируют простую электрическую цепь, включающую следующие компоненты:

• переменные источники;
• конденсатор;
• потребитель — обычно это лампочка.

Цепь с конденсатором Будучи включённым в переменную конденсатор время от времени перезаряжается, приобретая и отдавая заряды. Следовательно, происходит обмен электричеством между источником и двухполюсником, что приводит к формированию реактивной энергии.

Обратите внимание! Прибор не допускает пропускание по постоянной сети, поскольку в этом случае имеющееся сопротивление будет равно бесконечности. Если проходит переменный, то у сопротивления будет конечное значение

Сопротивление конденсатора.

Замкнем цепь. Конденсатор начал заряжаться и сразу стал источником тока, напряжения, Э. Д. С.. На рисунке видно что Э. Д. С. конденсатора направлена против заряжающего его источника тока.

Противодействие электродвижущей силы заряжаемого конденсатора заряду этого конденсатора называется емкостным сопротивлением.

Вся энергия затрачиваемая источником тока на преодоление емкостного
сопротивления превращается в энергию электрического поля конденсатора.
Когда конденсатор будет разряжаться вся энергия электрического поля
вернется обратно в цепь в виде энергии электрического тока. Таким
образом емкостное сопротивление является реактивным, т.е. не вызывающим безвозвратных потерь энергии.

Почему постоянный ток не проходит через конденсатор, а переменный ток проходит?

Включим цепь постоянного тока. Лампа вспыхнет и погаснет, почему? Потому что в цепи прошел ток заряда конденсатора. Как только конденсатор зарядится до напряжения батареи ток в цепи прекратится.

А теперь замкнем цепь переменного тока. В I четверти периода напряжение на генераторе возрастает от 0 до максимума. В цепи идет ток заряда конденсатора. Во II четверти периода напряжение на генераторе убывает до нуля. Конденсатор разряжается через генератор. После этого конденсатор вновь заряжается и разряжается. Таким образом в цепи идут токи заряда и разряда конденсатора. Лампочка будет гореть постоянно.

В цепи с конденсатором ток проходит во всей замкнутой цепи, в том числе и в диэлектрике конденсатора. В заряжающемся конденсаторе образуется электрическое поле которое поляризует диэлектрик. Поляризация это вращение электронов в атомах на вытянутых орбитах.

Одновременная поляризация огромного количества атомов образует ток, называемый током смещения.

Таким образом в проводах идет ток и в диэлектрике причем одинаковой величины.

конденсатора определяется по формуле

На активном сопротивлении напряжение U акт и ток I совпадают по фазе. На емкостном сопротивлении напряжение U c отстает от тока I на 90 0 . Результирующее напряжение приложенное генератором к конденсатору определяется по правилу параллелограмма. Это результирующее напряжение отстает от тока I на какой то угол φ всегда меньший 90 0 .

Общая концепция

Конденсатор состоит из двух проводящих обкладок и диэлектрика между ними. И все, больше ничего. С виду простая радиодеталь, но работает на высоких и низких частотах по-разному.
Обозначается на схеме двумя параллельными линиями.

Принцип работы

Эта радиодеталь хорошо демонстрирует явление электростатической индукции. Разберем на примере.

Если подключить к конденсатору постоянный источник тока, то в начальный момент времени ток начнет скапливаться на обкладках конденсатора. Это происходит за счет электростатической индукции. Сопротивление практически равно нулю.

Электрическое поле за счет электростатической индукции притягивает разноименные заряды на две противоположные обкладки. Это свойство материи называется емкостью. Емкость есть у всех материалов. И даже у диэлектриков, но у проводников она значительно больше. Поэтому обкладки конденсатора выполнены из проводника.

Основное свойство конденсатора — это емкость. Она зависит от площади пластин, расстояния между ними и материала диэлектрика, которым заполняют пространство между обкладками.

По мере накопления зарядов, поле начинает ослабевать, а сопротивление нарастает. Почему так происходит? Места на обкладках все меньше, одноименные заряды на них действуют друг на друга, а напряжение на конденсаторе становится равным источнику тока. Такое сопротивление называется реактивным, или емкостным. Оно зависит от частоты тока, емкости радиодеталей и проводов.

Когда на обкладках не останется места для электрического тока, то и ток в цепи прекратится. Электростатическая индукция пропадает. Теперь остается электрическое поле, которое держит заряды на своих обкладках и не отпускает их. А электрическому току некуда деваться. Напряжение на конденсаторе станет равным ЭДС (напряжению) источнику тока.

А что будет, если повысить ЭДС (напряжение) источника тока? Электрическое поле начнет все сильнее давить на диэлектрик, поскольку места на обкладках уже нет. Но если напряжение на конденсаторе превысит допустимые знания, то диэлектрик пробьет. И конденсатор станет проводником, заряды освободятся, и ток пойдет по цепи. Как тогда использовать конденсатор для высоких напряжений? Можно увеличить размер диэлектрика и расстояние между обкладками, но при этом уменьшается емкость детали.

Между обкладками находится диэлектрик, который препятствует прохождению постоянного тока. Это именно барьер для постоянного тока. Потому, что постоянный ток создает и постоянное напряжение. А постоянное напряжение может создавать электростатическую индукцию только при замыкании цепи, то есть, когда конденсатор заряжается.

Так конденсатор может сохранять энергию до тех пор, пока к нему не подключится потребитель.

Конденсатор и цепь постоянного тока

Добавим в схему лампочку. Она загорится только во время зарядки.
Еще одна важная особенность — когда происходит процесс зарядки током, то напряжение отстает от тока. Напряжение как бы догоняет ток, поскольку сопротивление нарастает плавно, по мере зарядки. Электрические зарядам нужно время, чтобы переместиться к обкладкам конденсатора. Так называется время зарядки. Оно зависит от емкости, частоты и напряжения.

По мере зарядки, лампочка начинает тусклее светиться.

Лампочка затухает при полной зарядке.

Постоянный электрический ток не проходит через конденсатор только после его зарядки.

Цепь с переменным током

А что если поменять полярность на источнике тока? Тогда конденсатор начнет разряжаться, и снова заряжаться, поскольку меняется полярность источника.

Электростатическая индукция возникает постоянно, если электрический ток переменный. Каждый раз, когда ток начинает менять свое направление, начинается процесс зарядки и разрядки.

Поэтому, конденсатор пропускает переменный электрический ток.

Чем выше частота — тем меньше реактивное (емкостное) сопротивление конденсатора.

Схема последовательного соединения

Когда применяется схема последовательного соединения конденсаторов, заряд каждой детали эквивалентен. С источником соединены только внешние пластины, другие – заряжаются перераспределением электрозарядов между ними. Все конденсаторы сохраняют аналогичное количество заряда на своих обкладках. Это объясняется тем, что на каждый последующий элемент поступает заряд от соседнего. Вследствие этого справедливо уравнение:

q = q1 = q2 = q3 = …

Известно, что при последовательном соединении резисторных элементов их сопротивления суммируются, но емкость конденсатора, включенного в такую электроцепь, рассчитывается по-другому.

Падение напряжения на отдельном конденсаторном элементе зависит от его емкости. Если в последовательной электроцепи имеется три конденсаторных элемента, составляется выражение для напряжения U на основании закона Кирхгофа:

U = U1 + U2 + U3,

при этом U= q/C, U1 = q/C1, U2 = q/C2, U3 = q/C3.

Подставляя значения для напряжений в обе части уравнения, получается:

q/C = q/C1 + q/C2 + q/C3.

Так как электрозаряд q – величина одинаковая, на нее можно поделить все части полученного выражения.

Результирующая формула для емкостей конденсаторов:

1/С = 1/С1 + 1/С2 + 1/С3.

Важно! Если конденсаторы подключаются в последовательную электроцепь, показатель, обратный результирующей емкости, равен совокупности обратных значений единичных емкостей. Особенности последовательного соединения

Особенности последовательного соединения

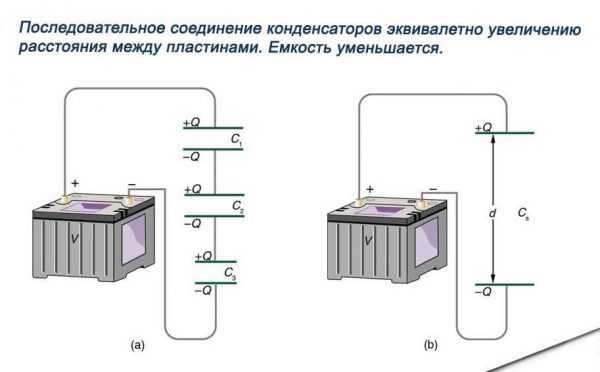
Особенности последовательного соединения

Пример. Три конденсаторных элемента подключены в последовательную цепь и обладают емкостями: С1 = 0,05 мкф, С2 = 0,2 мкФ, С3 = 0,4 мкФ. Рассчитать общую емкостную величину:

1. 1/С = 1/0,05 + 1/0,2 + 1/0,4 = 27,5;
2. С = 1/27,5 = 0,036 мкФ.

Важно! Когда конденсаторные элементы включены в последовательную электроцепь, общее емкостное значение не превышает наименьшей емкости отдельного элемента. Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:

Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:

Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:

С = (С1 х С2)/(С1 + С2).

В случае создания цепи из двух конденсаторов с идентичным емкостным значением:

С = (С х С)/(2 х С) = С/2.

Последовательно включенные конденсаторы имеют реактивное сопротивление, зависящее от частоты протекающего тока. На каждом конденсаторе напряжение падает из-за наличия этого сопротивления, поэтому на основе такой схемы создается емкостной делитель напряжения.

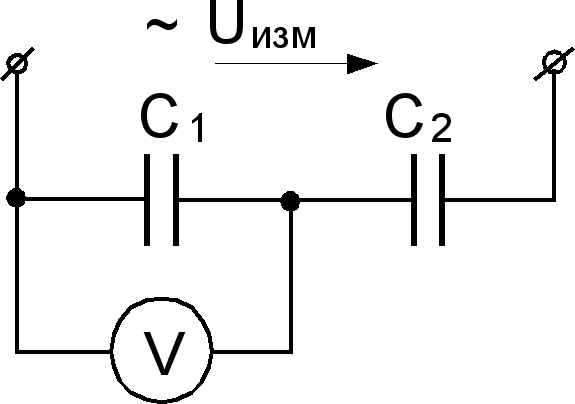
Емкостной делитель напряжения

Формула для емкостного делителя напряжения:

U1 = U x C/C1, U2 = U x C/C2, где:

• U – напряжение питания схемы;
• U1, U2 – падение напряжения на каждом элементе;
• С – итоговая емкость схемы;
• С1, С2 – емкостные показатели единичных элементов.

Вычисление падений напряжения на конденсаторах

К примеру, имеются сеть переменного тока 12 В и две альтернативных электроцепи подсоединения последовательных конденсаторных элементов:

• первая – для подключения одного конденсатора С1 = 0,1 мкФ, другого С2 = 0,5 мкФ;
• вторая – С1 = С2 = 400 нФ.

Первый вариант

1. Итоговая емкость электросхемы С = (С1 х С2)/(С1 + С2) = 0,1 х 0,5/(0,1 + 0,5) = 0,083 мкФ;
2. Падение напряжения на одном конденсаторе: U1 = U x C/C1 = 12 x 0,083/0,1 = 9,9 В
3. На втором конденсаторе: U2 = U x C/C2 = 12 х 0,083/0,5 = 1,992 В.

Второй вариант

1. Результирующая емкость С = 400 х 400/(400 + 400) = 200 нФ;
2. Падение напряжения U1 = U2 = 12 x 200/400 = 6 В.

Согласно расчетам, можно сделать выводы, что если подключаются конденсаторы равных емкостей, вольтаж делится поровну на обоих элементах, а когда емкостные значения различаются, то на конденсаторе с меньшей емкостной величиной напряжение увеличивается, и наоборот.

Ёмкостное сопротивление

Единицы измерения

Конденсатор, как обладатель электрической ёмкости, напоминает по своим показателям автомобильный аккумулятор. Но, в отличие от АКБ, ёмкостной заряд на нём держится совсем недолго, что объясняется наличием утечек в диэлектрике и частичной разрядкой через окружающую среду.

При этом ёмкость (как и у аккумулятора) определяет накопительные свойства конденсатора или его способность удерживать энергию между обкладками.

Обратите внимание! В системе СИ этот показатель измеряется в Фарадах, которые представляют собой очень крупную единицу измерения. На практике чаще всего пользуются более мелкими единицами измерения емкости, а именно:. На практике чаще всего пользуются более мелкими единицами измерения емкости, а именно:

На практике чаще всего пользуются более мелкими единицами измерения емкости, а именно:

• Пикофарады, соответствующие 10-12 Фарады (Ф);
• Нанофарады, равные 10-9Ф;
• Микрофарады (мкФ), составляющие 10-6 от Фарады.

Все эти единицы для кратности обозначаются как «пФ», «нФ» и «мФ» соответственно.

Пример расчета емкостного сопротивления

Иногда конденсаторы устанавливаются в цепочках гашения напряжения с целью получения меньших его значений (вместо понижающих трансформаторов).

Важно! Этот способ получения нужных напряжений считается не только очень простым, но и самым опасным, поскольку индуктивной развязки от высокого потенциала здесь не существует. Но если аккуратно обращаться с таким преобразователем, вполне можно будет собрать его своими руками. При расчёте требуемой ёмкости обычно исходят из следующих соображений:

При расчёте требуемой ёмкости обычно исходят из следующих соображений:

Но если аккуратно обращаться с таким преобразователем, вполне можно будет собрать его своими руками. При расчёте требуемой ёмкости обычно исходят из следующих соображений:

• Включаемый последовательно с нагрузкой конденсатор характеризуется импедансом, аналогом сопротивления для ёмкости;
• Этот показатель соответствует отдельному плечу в делителе напряжения, вторым элементом которого является сопротивление нагрузки;
• Соотношение сопротивлений обоих плеч выбирается с таким расчётом, чтобы на нагрузке осталось требуемое напряжение (12 Вольт, например), а весь остаток от 220 Вольт рассеивался бы на самом конденсаторе.

Дополнительная информация. Для улучшения переходных характеристик делительной цепочки иногда параллельно конденсатору включается ещё один из резисторов, называемый разрядным.

Схема для расчёта ёмкостного сопротивления

В нашем случае выбираются следующие данные:

• Uвх=220 Вольт;
• Uвых=12 Вольт;
• Iнагр=0,1Ампер (ток в нагрузке выбирается согласно её паспорта).

Исходя из них, можно определить значение сопротивления нагрузки:

Rн=220/0,1=2200 Ом или 2,2 Ком.

Для вычисления величины ёмкости, на которой должны «упасть» оставшиеся 208 Вольт, используются следующие показатели:

• Uс=208 Вольт;
• Iс=0,1Ампер;
• Fсети=50 Гц.

После этого можно вычислить омическое сопротивление конденсатора, достаточное для того, чтобы на нём было 208 Вольт:

Xc=Uс/Iс=208/0,1=2080.

Ёмкость конденсатора получается из рассмотренной ранее зависимости:

Xс=1/ ω C.

Исходя из этого, получим:

С = 1/Хс2 π Fсети = 1/2080х6, 28х50 = 0,0000015311 Фарады или 1,5 мкФ.

Сопротивление Rраз выбирается равным примерно 10 Ком или более.