Что такое разность потенциалов

Содержание:

Разница потенциалов в зависимости от напряжения

Разница потенциалов и напряжение — это два термина, которые используются в технике для описания разности потенциалов в двух точках. Напряжение относится к электричеству, где разность потенциалов может быть связана с электрическим, магнитным и гравитационным полями. Однако если рассматривать только электрическое поле, разность потенциалов такая же, как и напряжение.

Разность потенциалов

Потенциал — это понятие, используемое в электрическом, магнитном и гравитационном полях. Потенциал — это функция местоположения, а разность потенциалов между точкой A и точкой B рассчитывается путем вычитания потенциала A из потенциала B. Другими словами, гравитационная разность потенциалов между точками A и B — это объем работы, который должен быть выполняется для перемещения единицы массы (1 кг) из точки B в точку A. В электрическом поле это количество работы, которое необходимо совершить для перемещения единичного заряда (+1 кулон) из точки B в A. Разность гравитационных потенциалов равна измеряется в Дж / кг, где разность электрических потенциалов измеряется в В (вольтах).

Однако в общепринятом смысле термин «разность потенциалов» в основном используется для описания разности электрических потенциалов

Следовательно, мы должны использовать этот термин осторожно, чтобы избежать неверных толкований

напряжение

Разность электрических потенциалов между точками A и B также известна как напряжение между точками A и B. Напряжение измеряется в вольтах (В). Вольтметр — это оборудование, используемое для измерения напряжения. Батарея обеспечивает напряжение между двумя своими концами (электродами), и ее положительная сторона имеет более высокий потенциал, а отрицательный электрод — более низкий потенциал.

В цепи ток течет от более высокого потенциала к более низкому потенциалу. Когда он проходит через резистор, можно наблюдать напряжение между двумя концами. Это называется «падением напряжения». Хотя напряжение всегда находится между двумя точками, иногда люди просят напряжение точки. Речь идет о напряжении между этой конкретной точкой и контрольной точкой. Эта контрольная точка обычно «заземлена», и ее электрический потенциал считается равным 0 В.

В чем разница между разностью потенциалов и напряжением? 1. Разницу потенциалов можно найти в любом поле (гравитационном, электрическом, магнитном и т. Д.), А напряжение используется только для электрических полей. 2. Разность потенциалов по отношению к электрическому полю называется напряжением. 3. Напряжение измеряется в вольтах (В), а единица измерения разности потенциалов изменяется в зависимости от типа энергетического поля (В для электрического, Дж / кг для гравитационного и т. Д.).

Поток вектора магнитной индукции

Электростатическое поле характеризуется напряженностью, которая вместе с вектором электромагнитной индукции составляет электромагнитное поле.

Если заряженная частица движется в электромагнитном поле, то полную силу, которая воздействует на частицу, определяют по закону Лоренца:

где:

• q – величина заряда;
• v – скорость движения;
• E – величина электрического поля;
• В – вектор магнитной индукции.

Обратите внимание! В указанной формуле приведены векторные величины. Крестом обозначено векторное произведение. Силу F воздействия на частицу принято называть силой Лоренца

Силу F воздействия на частицу принято называть силой Лоренца.

Данная формула является наиболее общей и может использоваться для вычисления при условии точечного заряда (в том числе единичного).

Разность потенциалов. Напряжение

Работа сил электростатического поля по перемещению заряда q из точки 1 в точку 2 поля

\(~A_{12} = W_{p1} — W_{p2} .\)

Выразим потенциальную энергию через потенциалы поля в соответствующих точках:

\(~W_{p1} = q_0 \varphi_1 , W_{p2} = q_0 \varphi_2 .\)

Тогда

\(~A_{12} = q_0 (\varphi_1 — \varphi_2) .\)

Таким образом, работа определяется произведением заряда на разность потенциалов начальной и конечной точек.

Из этой формулы разность потенциалов

\(~\varphi_1 — \varphi_2 = \frac{A_{12}}{q_0} .\)

Разность потенциалов — это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду.

В СИ единицей разности потенциалов является вольт (В).

1 В — разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа в 1 Дж.

Разность потенциалов в отличие от потенциала не зависит от выбора нулевой точки. Разность потенциалов φ₁ — φ₂ часто называют электрическим напряжением между данными точками поля:

\(~U = \varphi_1 — \varphi_2 .\)

Напряжение между двумя точками поля определяется работой сил этого поля по перемещению заряда в 1 Кл из одной точки в другую. В электростатическом поле напряжение вдоль замкнутого контура всегда равно нулю.

Работу сил электрического поля иногда выражают не в джоулях, а в электронвольтах. 1 эВ равен работе, совершаемой силами поля при перемещении электрона (е = 1,6·10-19 Кл) между двумя точками, напряжение между которыми равно 1 В.

1 эВ = 1,6·10-19 Кл·1 В = 1,6·10-19 Дж.


1 МэВ = 106 эВ = 1,6·10-13 Дж.

Электрическое поле графически можно изобразить не только с помощью линий напряженности, но и с помощью эквипотенциальных поверхностей.

Эквипотенциальной называется воображаемая поверхность, в каждой точке которой потенциал одинаков. Разность потенциалов между двумя любыми точками эквипотенциальной поверхности равна нулю.

Следовательно, работа по перемещению заряда вдоль эквипотенциальной поверхности равна 0. Но работа рассчитывается по формуле \(~A = F \Delta r \cos \alpha = q_0E \Delta r \cos \alpha\). Здесь q ≠ 0, Е ≠ 0, Δr ≠ 0. Значит, \(~\cos \alpha = 0 \Rightarrow \alpha = 90^{\circ}\).

Следовательно, линии напряженности перпендикулярны эквипотенциальным поверхностям. Первая эквипотенциальная поверхность металлического проводника — это поверхность самого заряженного проводника, что легко проверить электрометром. Остальные эквипотенциальные поверхности проводятся так, чтобы разность потенциалов между двумя соседними поверхностями была постоянной.

Картины эквипотенциальных поверхностей некоторых заряженных тел приведены на рис. 3.

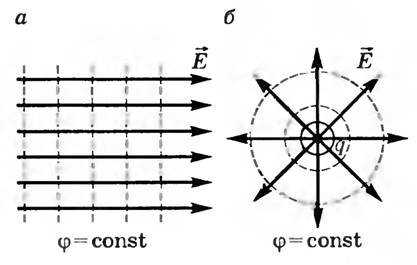
Рис. 3

Эквипотенциальными поверхностями однородного электростатического поля являются плоскости, перпендикулярные линиям напряженности (рис. 3, а).

Эквипотенциальные поверхности поля точечного заряда представляют собой сферы, в центре которых расположен заряд q (рис. 3, б).

Сила порождаемая электрическими зарядами

Напряженность электрического поля является векторной величиной, а значит имеет численную величину и направление. Величина напряженности электрического поля имеет свою размерность, которая зависит от способа ее вычисления.

Электрическая сила взаимодействия зарядов описывается как бесконтактное действие, а иначе говоря имеет место дальнодействие, то есть действие на расстоянии. Для того, чтобы описать такое дальнодействие удобно ввести понятие электрического поля и с его помощью объяснить действие на расстоянии.

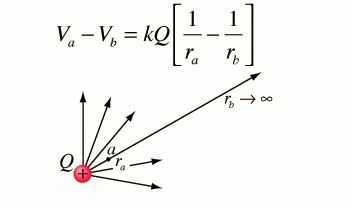
Давайте возьмем электрический заряд, который мы обозначим символом Q. Этот электрический заряд создает электрическое поле, то есть он является источником действия силы. Так как во вселенной всегда имеется хотя бы один положительный и хотя бы один отрицательный заряд, которые действую друг на друга на любом, даже бесконечно далеком расстоянии, то любой заряд является источником силы, а значит уместно описание создаваемого ими электрического поля. В нашем случае заряд Q является источником электрического поля и мы будем его рассматривать именно как источник поля.

Напряженность электрического поля источника заряда может быть измерена с помощью любого другого заряда, находящегося где-то в его окрестностях. Заряд, который используется для измерения напряженности электрического поля называют пробным зарядом, так как он используется для проверки напряженности поля. Пробный заряд имеет некоторое количество заряда и обозначается символом q.

При помещении пробного заряда в электрическое поле источника силы (заряд Q), пробный заряд будет испытывать действие электрической силы — или притяжения, или отталкивания. Силу можно обозначить как это обычно принять в физике символом F. Тогда величину электрического поля можно определить просто как отношение силы к величине пробного заряда.

Если напряженность электрического поля обозначается символом E, то уравнение может быть переписано в символической форме как

Стандартные метрические единицы измерения напряженности электрического поля возникают из его определения. Таким образом напряженность электрического поля определяется как сила равная 1 Ньютону (Н) деленному на 1 Кулон (Кл). Напряженность электрического поля измеряется в Ньютон/Кулон или иначе Н/Кл. В системе СИ также измеряется в Вольт/метр. Для понимания сути такого предмета как напряженность электрического поля гораздо важнее размерность в метрической системе в Н/Кл, потому как в такой размерность отражается происхождение такой характеристики как напряженность поля. Обозначение в Вольт/Метр делает понятие потенциала поля (Вольт) базовым, что в некоторых областях удобно, но не во всех.

В приведенном выше примере участвуют два заряда Q (источник) и q пробный. Оба этих заряда являются источником силы, но какой из них следует применять в вышеприведенной формуле? В формуле присутствует только один заряд и это пробный заряд q (не источник).

Напряженность электрического поля не зависит от количества пробного заряда q. На первый взгляд это может привести вас в замешательство, если, конечно, вы задумаетесь над этим. Беда в том, что не все имеют полезную привычку думать и пребывают в так называемом блаженном невежестве. Если вы не думаете, то и замешательства такого рода у вас и не возникнет. Так как же напряженность электрического поля не зависит от q, если q присутствует в уравнении? Отличный вопрос! Но если вы подумаете об этом немного, вы сможете ответить на этот вопрос. Увеличение количества пробного заряда q — скажем, в 2 раза — увеличится и знаменатель уравнения в 2 раза. Но в соответствии с Законом Кулона, увеличение заряда также увеличит пропорционально и порождаемую силу F. Увеличится заряд в 2 раза, тогда и сила F возрастет в то же количество раз. Так как знаменатель в уравнении увеличивается в два раза (или три, или четыре), то и числитель увеличится во столько же раз. Эти два изменения компенсируют друг друга, так что можно смело сказать, что напряженность электрического поля не зависит от количества пробного заряда.

Таким образом, независимо от того, какого количества пробный заряд q используется в уравнении, напряженность электрического поля E в любой заданной точке вокруг заряда Q (источника) будет одинаковой при измерении или вычислении.

Разность потенциалов

Если две точки обладают определённым потенциалом, и если они не равны, то говорят о том, что между двумя точками существует разность потенциалов. Разность потенциалов возникает между точками:

• потенциал которых определяется зарядами разных знаков;
• точкой с потенциалом от заряда любого знака и точкой с нулевым потенциалом;
• точками, имеющими потенциал равного знака, но отличающимися по модулю.

То есть, разность потенциалов не зависит от выбора системы координат. Можно провести аналогию с бассейнами с водой, расположенными на разной высоте относительно нулевой отметки (например, уровня моря).

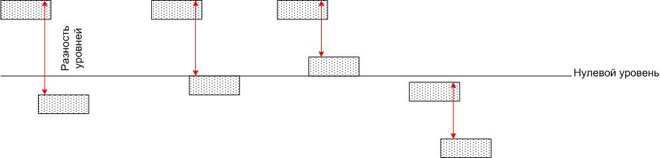
Вода каждого бассейна имеет определенную потенциальную энергию, но если соединить два любых бассейна трубкой, то в каждой из них возникнет поток воды, расход которой определяется не только размерами трубки, но и разностью потенциальных энергий в гравитационном поле Земли (то есть, разностью высот). Абсолютное значение потенциальных энергий значения в данном случае не имеет.

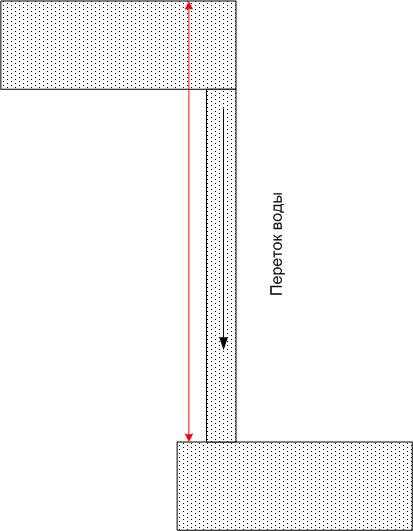
Точно так же, если соединить проводником две точки с разным потенциалом, по нему потечёт электрический ток, определяемый не только сопротивлением проводника, но и разностью потенциалов (но не их абсолютным значением). Продолжая аналогию с водой, можно сказать, что вода в верхнем бассейне скоро закончится, и если не найдется той силы, которая переместит воду обратно наверх (например, насоса), то и поток очень быстро прекратится.

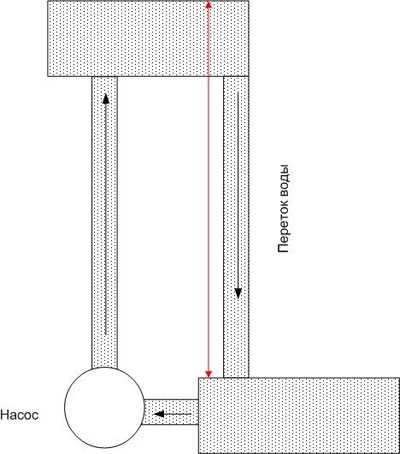
Так и в электрической цепи – чтобы поддерживать разность потенциалов на определенном уровне, потребуется сила, переносящая заряды (точнее, носители зарядов) к точке с наибольшим потенциалом. Такая сила называется электродвижущей силой и сокращенно обозначается ЭДС. ЭДС может носить различную природу – электрохимическую, электромагнитную и т.п.

На практике имеет значение в основном разность потенциалов между начальной и конечной точками траектории движения носителей зарядов. В этом случае эту разность называют напряжением, и оно в СИ также измеряется в вольтах. О напряжении в 1 Вольт можно говорить, если поле совершает работу в 1 Джоуль при перемещении заряда в 1 Кулон из одной точки в другую, то есть 1В=1Дж/1Кл, и Дж/Кл также может являться единицей измерения разности потенциалов.

Электризация тел

Электризация – процесс сообщения телу электрического заряда, т. е. нарушение его электрической нейтральности. Процесс электризации представляет собой перенесение с одного тела на другое электронов или ионов. В результате электризации тело получает возможность участвовать в электромагнитном взаимодействии.

Способы электризации:

• трением, – например, электризация эбонитовой палочки при трении о мех. При тесном соприкосновении двух тел часть электронов переходит с одного тела на другое; в результате этого на поверхности у одного из тел создается недостаток электронов и тело получает положительный заряд, а у другого – избыток, и тело заряжается отрицательно. Величины зарядов тел одинаковы;
• через влияние (электростатическая индукция) – тело остается электрически нейтральным, электрические заряды внутри него перераспределяются так, что разные части тела приобретают разные по знаку заряды;
• при соприкосновении заряженного и незаряженного тела – заряд при этом распределяется между этими телами пропорционально их размерам. Если размеры тел одинаковы, то заряд распределяется между ними поровну;
• при ударе;
• под действием излучения – под действием света с поверхности проводника могут вырываться электроны, при этом проводник приобретает положительный заряд.

Потенциал. Разность потенциалов. Напряжение.Эквипотенциальные поверхности

Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной.

За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора.

— следствие принци­па суперпозиции полей (потенциалы складываютсяалгебраически).

Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность.

В СИ потенциал измеряется в вольтах:

Разность потенциалов

Напряжение — разность значений потенциала в начальной и конечнойточках траектории.

Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля.

Разность потенциалов (напряжение) не зависит от выбора

Единица разности потенциалов

Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.

Связь между напряженностью и напряжением.

Из доказанного выше: →

напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d).

Из этого соотношения видно:

1. Вектор напряженности направлен в сторону уменьшения потенциала.
2. Электрическое поле существует, если существует разность потенциалов.
3. Единица напряженности: — Напряженность поля равна1 В/м, если между двумя точками поля, находящимися на расстоянии 1 м друг от друга существует разность потенциалов 1 В.

Эквипотенциальные поверхности.

ЭПП — поверхности равного потенциала.

— работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается;

— вектор напряженности перпендикулярен к ЭПП в каждой ее точке.

Измерение электрического напряжения (разности потенциалов)

Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр.

Потенциальная энергия взаимодействия зарядов.

Потенциал поля точечного заряда

Потенциал заряженного шара

а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (. ) и равны потенциалу на поверхности шара.

б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда.

Перераспределение зарядов при контакте заряженных проводников.

Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными.

Характеристики электрического поля

Электрическое поле описывается векторной величиной – напряженностью. Стрелка, направление которой совпадает с силой, действующей в точке на единичный положительный заряд, длина пропорциональна модулю силы. Физики находят удобным пользоваться потенциалом. Величина скалярная, проще представить на примере температуры: в каждой точке пространства некоторое значение. Под электрическим потенциалом понимают работу, совершаемую для перемещения единичного заряда из точки нулевого потенциала в данную точку.

Электрический потенциал

Поле, описываемое указанным выше способом, называется безвихревым. Иногда именуют потенциальным. Функция потенциала электрического поля непрерывная, изменяется плавно по протяженности пространства. В результате выделим точки равного потенциала, складывающие поверхности. Для единичного заряда сфера: дальше объект, слабее поле (закон Кулона). Поверхности называют эквипотенциальными.

Для понимания уравнений Максвелла заимейте представление о нескольких характеристиках векторного поля:

Градиентом электрического потенциала называется вектор, направление совпадает с наискорейшим ростом параметра поля. Значение тем больше, чем быстрее изменяется величина. Направлен градиент от меньшего значения потенциала к большему:

1. Градиент перпендикулярен эквипотенциальной поверхности.
2. Градиент тем больше, чем ближе расположение эквипотенциальных поверхностей, отличающихся друг от друга на заданную величину потенциала электрического поля.
3. Градиент потенциала, взятый с обратным знаком, является напряженностью электрического поля.

Электрический потенциал. Градиент “взбирается в гору”

• Дивергенция является скалярной величиной, вычисляемой для вектора напряженности электрического поля. Является аналогом градиента (для векторов), показывает скорость изменения величины. Необходимость во введении дополнительной характеристики: векторное поле лишено градиента. Следовательно, для описания требуется некий аналог – дивергенция. Параметр в математической записи схож с градиентом, обозначается греческой буквой набла, применяется для векторных величин.
• Ротор векторного поля именуется вихрем. Физически величина равна нулю при равномерном изменении параметра. Если ротор отличен от нуля, возникают замкнутые изгибы линий. У потенциальных полей точечных зарядов по определению вихрь отсутствует. Не обязательно линии напряжённости в этом случае прямолинейны. Просто изменяются плавно, не образуя вихрей. Поле с ненулевым ротором часто называют соленоидальным. Часто применяется синоним – вихревое.
• Полный поток вектора представлен интегралом по поверхности произведения напряженности электрического поля на элементарную площадь. Предел величины при стремлении емкости тела к нулю представляет собой дивергенцию поля. Понятие предела изучается старшими классами средней школы, ученик может составить некоторое представление на предмет обсуждения.

Уравнения Максвелла описывают изменяющееся во времени электрическое поле и показывают, что в таких случаях возникает волна. Принято считать, одна из формул указывает отсутствие в природе обособленных магнитных зарядов (полюсов). Иногда в литературе встретим особый оператор – лапласиан. Обозначается как квадрат набла, вычисляется для векторных величин, представляет дивергенцией градиента поля.

Подобные аксиомы легко положим в основу описания процессов, происходящих в реальных существующих устройствах. Антигравитационный, вечный двигатель были бы неплохим подспорьем экономике. Если реализовать на практике теорию Эйнштейна никому не удалось, наработки Николы Тесла исследуются энтузиастами. Отсутствуют ротор, дивергенция.

Для чего нужен потенциометр электрику

Что такое коэффициент мощности

Данный прибор широко применяется в практике для модуляции напряжения. Дело в том, что у многих источников (особенно заточенных под автономное функционирование: аккумуляторные элементы, солнечные батареи и т.д.) константное напряжение, не поддающееся управлению без специальных устройств, что может вызвать проблемы. Чтобы уменьшить исходное напряжение такого элемента, используют устройства-делители, снабженные потенциометрами.

Потенциометр-реостат

Как работает потенциометр? Он представляет собой резистор, имеющий пару выводов и подвижный ползунок с еще одним выводом. Подключаться такое переменное устройство сопротивления может двумя способами:

1. По типу реостата, с использованием ползункового вывода и одного из пары других. Сопротивление замеряется движением ползунка по корпусу резистора. Регуляция цепного электротока в таком случае возможна при последовательном подключении такого реостата и источника напряжения.
2. Потенциометрическим методом, задействующим каждый вывод из имеющейся у прибора тройки. Два главных вывода включаются параллельно источнику, снятие сниженного напряжения реализуется с ползункового механизма и одного вывода. В этом случае через резисторное устройство течет электроток, создающий спад напряжения между ползунком и боковыми выводами. В такой модели на источник питания ложится большая нагрузка, так как для точности регуляции и отсутствия сбоев необходимо, чтобы резисторное сопротивление в несколько раз уступало нагрузочному.

Потенциометрическое подключение прибора

Таким образом, понятие потенциала используется в разных областях физики: как в механике, так и в изучении электричества. В последнем случае оно выступает в качестве характеристики поля. Непосредственно рассматриваемая величина измерению не поддается, зато можно измерить разность, тогда один заряд берется за точку отсчета.

Измерение потенциалов точек электрической цепи и построение потенциальной диаграммы

Фрагмент текста работы

любой ветви схемы можно найти по закону Ома для участка цепи, содержащего ЭДС. Для того чтобы можно было применить закон Ома, необходимо знать потенциалы узлов схемы. Метод расчета электрических цепей, в котором за неизвестные принимают потенциалы узлов схемы, называют методом узловых потенциалов.

Допустим, что в схеме n узлов. Так как любая (одна) точка схемы может быть заземлена без изменения токораспределения в схеме, то один из узлов схемы можно мысленно заземлить, т. е. принять потенциал его равным нулю. При этом число неизвестных уменьшается с n до n-1.

Число неизвестных в методе узловых потенциалов равно числу уравнений, которые необходимо составить для схемы по первому закону Кирхгофа. Метод узловых потенциалов, как и метод контурных токов, — один из основных расчетных приемов. В том случае, когда число узлов без единицы меньше числа независимых контуров в схеме, данный метод является более экономичным, чем метод контурных токов.

Вывод основных расчетных уравнений проведем применительно к схеме рис. 2, в которой три узла. Если узел 3 мысленно заземлить, т. е. принять =0, то необходимо определить потенциалы только двух узлов: , .

Запишем уравнения по первому закону Кирхгофа для независимых узлов, причем токи, направленные к узлу берем со знаком минус, а от узла – со знаком плюс.

Для первого узла ,

Для второго узла .

Рис. 2. Схема для расчета по методу узловых потенциалов

Запишем токи по закону Ома:

Подставим токи в уравнения по первому закону Кирхгофа:

G11— сумма проводимостей ветвей, сходящихся в первом узле,

G12— сумма проводимостей ветвей, соединяющих первый и второй узлы, взятая со знаком минус,

G21— сумма проводимостей ветвей, соединяющих первый и второй узлы, взятая со знаком минус,

G11— сумма проводимостей ветвей, сходящихся во втором узле,

I11— узловой ток первого узла,

I22 — узловой ток второго узла.

Запишем уравнения в матричной форме:

Решим эти уравнения относительно искомых потенциалов и выразим токи ветвей, используя закон Ома.

После нахождения токов ветвей любым методом всегда делается проверка по первому закону Кирхгофа.

Чем отличается ЭДС от напряжения

Интересно многие сразу поняли, в чем разница между ЭДС и напряжением? И никого не поправлял учитель (учительница) по физике, когда на практических занятиях говорил (-ла) о том, что мы подключаем именно источник ЭДС, а не напряжения? В большинстве случаев мы с вами путались, потому что и ЭДС, и напряжение измеряется в Вольтах. Так давайте все-таки разберемся, чем принципиально отличается ЭДС от напряжения.

Что такое ЭДС

Итак, для начала давайте разберемся, что такое ЭДС. Электродвижущая сила (ЭДС) — это такая физическая величина, которая характеризует работу сторонних (не потенциальных) сил в источниках переменного либо же постоянного тока.

В замкнутой цепи ЭДС — это работа сил, совершаемая для перемещения единичного заряда вдоль всего контура.

Из выше представленного определения вытекает следующее: источниками ЭДС являются силы, которые не имеют прямое отношение к электростатике, но при этом они являются силами, которые создают движение заряда в замкнутой электрической цепочке.

yandex.ru

Например, при механическом вращении обмотки ротора в электромагнитном поле, в ней будет формироваться индукционная ЭДС. При этом формирование ЭДС будет проходить в каждом витке отдельно, но при этом электродвижущая сила соседних витков будет складываться, и на выходе мы будем иметь сумму ЭДС всех витков.

Если посмотреть на аккумуляторные батареи, то в них источником ЭДС является химическая реакция.

Кроме этого источниками могут выступать так называемые элементы Пельтье, в которых ЭДС образуется при термическом нагреве.

Пьезоэффект (когда при механическом воздействии на материал на его концах образуется разность потенциалов) также относится к источникам ЭДС. Впрочем, как и фотоэффект.

yandex.ru

Из выше представленных примеров видно, что, применяя различные материалы и способы их взаимодействия, можно получить ЭДС, способную организовать упорядоченное движение заряженных частиц в замкнутом контуре

Условно принято считать, что ЭДС — это работа в 1 Джоуль, совершаемая при перемещении заряда в 1 Кулон и измеряется в Вольтах.

ЭДС = 1Джоуль/1Кулон= 1 Вольт.
Ну а теперь давайте переключим свое внимание на напряжение.

Что такое напряжение

Итак, напряжение измеряется в аналогичных величинах, то есть в Вольтах. И напряжение — это разница потенциалов между двумя точками цепочки. Причем данные потенциалы рассматриваются только в электростатическом поле.

Получается, если мы с вами будем перемещать заряд величиной в 1 Кулон и точку №1 в точку №2, мы так же будем совершать работу в 1 Джоуль, при том условии, что разница потенциалов между точками будет равна 1 Вольт.

Вроде одно и то же, но в случае с напряжением обязательным условием является наличие электростатического поля. А откуда оно взялось? Так вот источником этого поля и является подключенный к цепи источник ЭДС.

Если провести аналогию с водонапорной башней, то можно представить следующую картинку:

yandex.ru

Получается, если мы с вами возьмем любой гальванический элемент, например, батарейку и измерим с помощью мультиметра его напряжение без подключенной нагрузки, то таким образом мы получим величину ЭДС.

Если же мы с вами создадим замкнутую цепь, в которую будет включена любая нагрузка, то, измеряя напряжение на тех же выводах батарейки, мы с вами увидим уже напряжение, и оно будет несколько меньше чем величина ЭДС.

Это связано с тем, что внутри любого источника ЭДС присутствует внутреннее сопротивление и когда мы подключаем нагрузку, происходит падение напряжения не только на концах нагрузки, но и на самом внутреннем сопротивлении источника ЭДС.

Электрическая емкость. Конденсатор

Электрическая емкость (электроемкость) – скалярная физическая величина, характеризующая способность уединенного проводника удерживать электрический заряд.

Обозначение – ​\( C \)​, единица измерения в СИ – фарад (Ф).

Уединенный проводник – это проводник, удаленный от других проводников и заряженных тел.

Фарад – электроемкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл:

Формула для вычисления электроемкости:

где ​\( q \)​ – заряд проводника, ​\( \varphi \)​ – его потенциал.

Электроемкость зависит от его линейных размеров и геометрической формы. Электроемкость не зависит от материала проводника и его агрегатного состояния. Электроемкость проводника прямо пропорциональна диэлектрической проницаемости среды, в которой он находится.

Конденсатор – это система из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Проводники называют обкладками конденсатора. Заряды обкладок конденсатора равны по величине и противоположны по знаку заряда. Электрическое поле сосредоточено между обкладками конденсатора. Конденсаторы используют для накопления электрических зарядов.

Электроемкость конденсатора рассчитывается по формуле:

где ​\( q \)​ – модуль заряда одной из обкладок,
​\( U \)​ – разность потенциалов между обкладками.

Электроемкость конденсатора зависит от линейных размеров и геометрической формы и расстояния между проводниками. Электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости вещества между проводниками.

Плоский конденсатор представляет две параллельные пластины площадью ​\( S \)​, находящиеся на расстоянии ​\( d \)​ друг от друга.

Электроемкость плоского конденсатора:

где ​\( \varepsilon \)​ – диэлектрическая проницаемость вещества между обкладками,\( \varepsilon_0 \) – электрическая постоянная.

На электрической схеме конденсатор обозначается:

Виды конденсаторов:

• по типу диэлектрика – воздушный, бумажный и т. д.;
• по форме – плоский, цилиндрический, сферический;
• по электроемкости – постоянной и переменной емкости.

Конденсаторы можно соединять между собой.

Параллельное соединение конденсаторов

При параллельном соединении конденсаторы соединяются одноименно заряженными обкладками. Напряжения конденсаторов равны:

Общая емкость:

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов соединяют их разноименно заряженные обкладки.

Заряды конденсаторов при таком соединении равны:

Общее напряжение:

Величина, обратная общей емкости:

При таком соединении общая емкость всегда меньше емкостей отдельных конденсаторов.

Важно!
Если конденсатор подключен к источнику тока, то разность потенциалов между его обкладками не изменяется при изменении электроемкости и равна напряжению источника. Если конденсатор заряжен до некоторой разности потенциалов и отключен от источника тока, то его заряд не изменяется при изменении электроемкости

Применение конденсаторов
Конденсаторы используются в радиоэлектронных приборах как накопители заряда, для сглаживания пульсаций в выпрямителях переменного тока.

Понятие потенциала в физике

Что такое потенциал в физике? Это понятие очень часто применяется для описания качеств сил и полей самой разной природы. Скалярная функция, характеризующая некоторую величину, представляющуюся вектором, – вот что это потенциал. Гравитационный потенциал описывает соответствующее поле. В термодинамике это понятие применяется для системной внутренней энергии, в механике – для той или иной приложенной к предмету силы.

Электрика, прежде всего, интересует, что такое потенциал в электричестве. Из общего определения нетрудно вывести, что характеристика электрополя – это электрический потенциал. В своей статической форме электрический потенциал показывает потенциальную энергию одиночного «плюсового» заряда, помещаемого в данное место электрополя, и является одной из разновидностей электромагнитного потенциала. Вторая его форма – векторная (в отличие от скалярной), описывает магнитное поле.

Важно! Характеристика поля, описывающая зависимость работы при передвижении исключительно от исходной точки и места назначения, – это потенциальность поля. Траектория перемещения в этом случае на работу не влияет