Электростатика

Разность потенциалов

Потенциал электрического поля. Разность потенциалов

Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.

Обозначение – \( \varphi \), единица измерения в СИ – вольт (В).

Потенциал \( \varphi \) является энергетической характеристикой электростатического поля.

Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:

Обозначение – \( \Delta\varphi \), единица измерения в СИ – вольт (В).

Иногда разность потенциалов обозначают буквой \( U \) и называют напряжением.

Важно!
Разность потенциалов \( \Delta\varphi=\varphi_1-\varphi_2 \), а не изменение потенциала \( \Delta\varphi=\varphi_2-\varphi_1 \). Тогда работа электростатического поля равна:. Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки

Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле. В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность

В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал поля точечного заряда \( q \) в точке, удаленной от него на расстояние \( r \), вычисляется по формуле:

Для наглядного представления электрического поля используют эквипотенциальные поверхности.

Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (\( r =R \), где \( R \) – радиус шара). Напряженность поля внутри шара равна нулю. Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.

Свойства эквипотенциальных поверхностей

Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.

Разность потенциалов и напряженность связаны формулой:

Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:

Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.

Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.

Алгоритм решения таких задач:

установить характер и особенности электростатических взаимодействий объектов системы;
ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
записать законы сохранения и движения для объектов;
выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
составить систему уравнений и решить ее относительно искомой величины;
проверить решение.

Нужны ли устройства компенсации в быту?

На первый взгляд в домашней сети не должно быть больших реактивных токов. В стандартном наборе бытовых потребителей преобладают электрическая техника с резистивными нагрузками:

электрочайник (P f = 1);
лампы накаливания (P f = 1);
электроплита (P f = 1) и другие нагревательные приборы;

Коэффициенты мощности современной бытовой техники, такой как телевизор, компьютер и т.п. близки к 1. Ими можно пренебречь.

Но если речь идёт о холодильнике (P f = 0,65), стиральной машине и микроволновой печи, то уже стоит задуматься об установке синхронных компенсаторов. Если вы часто пользуетесь электроинструментом, сварочным аппаратом или у вас дома работает электронасос, тогда установка устройства компенсации более чем желательна.

Экономический эффект от установки таких устройств ощутимо скажется на вашем семейном бюджете. Вы сможете экономить около 15% средств ежемесячно. Согласитесь, это не так уж мало, учитывая тарифы не электроэнергию.

Попутно вы решите следующие вопросы:

уменьшение нагрузок на индуктивные элементы и на проводку;
улучшение качества тока, способствующего стабильной работе электронных устройств;
понижение уровня высших гармоник в бытовой сети.

Для того чтобы ток и напряжение работали синфазно, устройства компенсации следует размещать как можно ближе к потребителям тока. Тогда реальная отдача индуктивных электроприёмников будет принимать максимальные значения.

В чем физический смысл активной, реактивной и полной мощностей? Назовите единицы измерения?

Активная мощность потребляется в активных сопротивлениях, и, в конечном итоге, за счет нее выполняется механическая работа или происходит нагревание резисторов. Реактивная мощность-эта та мощность, которая попросту «болтается в проводах». Она не потребляется активно цепью, но системы передачи оказываются ею загруженными.

Пусть приемник электроэнергии присоединен к источнику синусоидального напряжения u(t) = Usin(ωt) и потребляет синусоидальный ток i(t) = I sin (ωt -φ), сдвинутый по фазе относительно напряжения на угол φ. U и I – действующие значения. Значение мгновенной мощности на зажимах приемника определяется выражением

p(t) = u(t) ∙i(t) = 2UI sin(ωt) sin(ωt -φ) = UI cosφ — UI cos(2ωt -φ)

(5.1)

и является суммой двух величин, одна из которых постоянна во времени, а другая пульсирует с двойной частотой.

Среднее значение p(t)

за период Т называется активной мощностью и полностью определяется первым слагаемым уравнения (5.1):

Активная мощность характеризует энергию, расходуемую необратимо источником в единицу времени на производство полезной работы потребителем. Активная энергия, потребляемая электроприёмниками, преобразуется в другие виды энергии: механическую, тепловую, энергию сжатого воздуха и

Среднее значение от второго слагаемого мгновенной мощности (1.1) (пульсирует с двойной частотой) за время Т равно нулю, т. е. на ее создание не требуется каких-либо материальных затрат и поэтому она не может совершать полезной работы. Однако ее присутствие указывает, что между источником и приемником происходит обратимый процесс обмена энергией. Это возможно, если имеются элементы, способные накапливать и отдавать электромагнитную энергию – емкость и индуктивность. Эта составляющая характеризует реактивную мощность.

Полную мощность на зажимах приемника в комплексной форме можно представить следующим образом:

Единица измерения полной мощности S = UI – ВА.

Реактивная мощность – величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями (обменом) энергии между источником и приемником. Для синусоидального тока она равна произведению действующих значений тока I

и напряженияU на синус угла сдвига фаз между ними:Q =UI sinφ. Единица измерения – В∙Ар.

Реактивная мощность не связана с полезной работой ЭП и расходуется только на создание переменных электромагнитных полей в электродвигателях, трансформаторах, аппаратах, линиях и т. д.

Для реактивной мощности приняты такие понятия, как генерация, потребление, передача, потери, баланс. Считается, что если ток отстает по фазе от напряжения (индуктивный характер нагрузки), то реактивная мощность потребляется и имеет положительный знак, а если ток опережает напряжение (емкостный характер нагрузки), то реактивная мощность генерируется и имеет отрицательное значение.

Основными потребителями реактивной мощности на промышленных предприятиях являются асинхронные двигатели (60–65 % общего потребления), трансформаторы (20–25 %), вентильные преобразователи, реакторы, воздушные электрические сети и прочие приемники (10 %).

Передача реактивной мощности загружает электрические сети и установленное в ней оборудование, уменьшая их пропускную способность. Реактивная мощность генерируется синхронными генераторами электростанций, синхронными компенсаторами, синхронными двигателями (регулирование током возбуждения), батареями конденсаторов (БК) и линиями электропередачи.

Реактивная мощность, вырабатываемая емкостью сетей, имеет следующий порядок величин: воздушная линия 20 кВ генерирует 1 кВ∙Ар на 1 км трехфазной линии; подземный кабель 20 кВ – 20 кВ∙Ар/км; воздушная линия 220 кВ – 150 кВ∙Ар/км; подземный кабель 220 кВ – 3 МВ∙Ар/км.

Диэлектрики в электростатике

Кроме того, у направляющих есть ещё одна группа тел — это диэлектрики. Для начала необходимо уточнить разницу между диэлектриком и проводником. Проводники — это тела, в которых заряды могут свободно перемещаться. Примером проводника является медный провод. Если положить на него груз, а затем дотронуться до него рукой, то этот груз будет «всплывать» из проводника и, следовательно, разгрузит его.

Но если положительно электрифицировать стекло, которое является диэлектриком, то прикосновение через руку не приведёт к его разрядке. Электроны от конечности будут течь только в точке контакта, но это стекло будет по-прежнему наэлектризовано в местах, где к нему прикасаются.

Электроны в диэлектрике не могут свободно двигаться. Они ограничены атомами и молекулами, которые не могут покинуть. Но если поместить диэлектрик в поле разрядов между положительным и отрицательным зарядом, это расположение электронов и атомных ядер изменится. Эти частицы ведут себя как диполи. Такая позиция показывает все молекулы в диэлектрике.

Образуется цепочка диполей с зарядами, положительными с одной стороны, и отрицательными — с другой. Это явление называется диэлектрической поляризацией. Поляризованный диэлектрик создаёт своё поле, внутреннее, и у него вектор напряжённости всегда направлен противоположно полю, в котором расположен диэлектрик. Таким образом, вред от аварий при напряжении поля уменьшается.

О природе реактивной энергии

Для следующих двух четвертьпериодов вышеописанная история повторяется с тем лишь различием, что токи заряда и разряда емкости потекут в противоположных направлениях. В случае включения вместо конденсатора катушки индуктивности, суть процесса не изменится.

В этом и состоит главный фокус реактивной энергии — в момент ‘прилива’ мы заполняем свои цистерны

, в момент отлива же, мысливаем их содержимое обратно . Как можно заметить из этой простой аналогии, мы просто туда-сюда переливаем жидкость(или ток в электроцепях) . Если же мы соблазнимся слить хоть немного жидкости ‘налево’(включить последовательно с реактивным конденсатором активный резистор) , то мы станем брать‘несколько больше’ чем возвращать, а это‘несколько больше’ уже является активной энергией по определению(ведь мы эту часть не возвращаем обратно, не так ли?) , за которую как известно, приходится платить.

Или иной пример: предположим, что мы берем у кредитора некоторую сумму денег взаймы и сразу же возвращаем ему взятый только что кредит. Если мы отдадим ровно столько, сколько взяли (чистая реактивность) — мы придем к исходному состоянию и никто никому не будет ничего должен. В случае же, если мы потратим часть кредита на какую ни будь покупку и вернем то, что осталось от кредита после совершения покупки (добавим в цепь активную нагрузку и часть энергии уйдет из системы)

— мы будем все еще должны. Эта потраченная часть является активной составляющей взятого нами кредита.

Теперь у вас может возникнуть один весьма резонный вопрос — если все так просто, и для того чтобы энергия считалась реактивной, ее просто нужно полностью вернуть обратно источнику, почему предприятия вынуждены платить за потребляемую (и полностью возвращаемую)

реактивную энергию?

Все дело в том, что в случае чисто реактивной нагрузки, момент максимально потребляемого тока (реактивного)

приходится на момент минимального значения напряжения, и наоборот, в момент максимума напряжения на клеммах нагрузки, протекающий через нее ток равен нулю.

Протекающий реактивный ток греет питающие проводники — но это активные потери, вызванные протеканием реактивного тока по проводникам с ограниченной проводимостью, что эквивалентно последовательно включенным с реактивной нагрузкой активным резистором. Так же, поскольку в момент максимума реактивного тока напряжение на полюсах реактивного элемента переходит через ноль, активная мощность подводимая к нему в этот момент (произведение тока и напряжения)

равна нулю. Вывод — реактивный ток вызывает нагрев проводов, не совершая при этом никакой полезной работы. Следует заметить, что эти потери так-же является активными и будут засчитываться бытовым счетчиком активной энергии.

Большие предприятия сопсобны генерировать достаточно большие реактивные токи, которые отрицательно сказываются на функционировании энергосистемы. По этой причине, для них проводится учет как активной, так и реактивной составляющей потребленной энергии. Для уменьшения генерации реактивных токов (вызывающих вполне реальные активные потери)

, на предприятиях размещают установки компенсации реактивной мощности.

Баланс мощностей в электрической цепи постоянного тока

Баланс мощностей в электрической цепи означает, что мощность, которую выделяют все источники энергии, равна мощности, которую потребляют в этой же цепи все приемники энергии:

где – мощность i-

го источника ЭДС или тока, Вт; – мощность, выделяемая вj- м сопротивлении, Вт.

Очевидно, что баланс мощностей следует из закона сохранения энергии.

Запишем для анализируемой цепи рис. 2.15 сумму мощностей, выделяемых всеми источниками энергии. При этом мощности, выделяемые источниками ЭДС и тока, будем считать положительными, если ток в ветви, где установлен источник ЭДС или тока, совпадает с направлением тока внутри источника (со стрелкой в обозначении источника ЭДС или тока), и отрицательными, если направление тока в ветви противоположно направлению тока в источнике. Тогда, составив соответствующее уравнение для вычисления суммарной мощности, отдаваемой источниками ЭДС и тока в анализируемую цепь и подставив в него численные значения, получим суммарную мощность источников:

при этом токи ветвей должны подставляться в уравнение (2.70) со своим знаком, который получился при их расчете.

Суммарная мощность, рассеиваемая в цепи сопротивлениями (приемниками энергии), для той же цепи рис. 2.15, может быть найдена так:

В результате расчета (2.70) – выделяемая источниками мощность, и (2.71) – потребляемая сопротивлениями мощность в цепи – должны быть одинаковы.

Потенциальная диаграмма электрической цепи

Постоянного тока

Потенциальная диаграмма контура электрической цепи постоянного тока – это графическое изображение второго закона Кирхгофа, в котором вместо падений напряжений записаны потенциалы узлов электрической цепи.

Она показывает суммарное значение потенциала и суммарное сопротивление в данной точке цепи того контура, для которого построена диаграмма, считая от опорного узла, потенциал которого принят за нулевой. Иными словами, потенциальная диаграмма показывает распределение потенциалов и сопротивлений в том контуре цепи, для которого она построена.

Графически эта диаграмма представляет собой ломаную линию, изображенную в декартовой системе координат, горизонтальной осью которой (осью абсцисс) является ось сопротивлений , а вертикальной осью (осью ординат) – ось потенциалов .

Процесс построения потенциальной диаграммы электрической цепи рассмотрим для той же, что и ранее, электрической цепи, показанной на рис. 2.3, и модифицированной для удобства построения потенциальной диаграммы так, как показано на рис. 2.15.

Поскольку для построения потенциальной диаграммы требуется знание численных значений токов ветвей и сопротивлений ветвей, приведем эти численные значения для цепи рис. 2.15 при условии, что исходные данные для расчета этой цепи таковы: Ом, Ом, Ом, Ом, Ом, Ом; величины источников ЭДС: В, В; величины источников тока: А, А. Значения токов в ветвях цепи, рассчитанные прямым применением законов Кирхгофа (сам расчет здесь не приводится), таковы: ; ; ; ; ; .

Построение потенциальной диаграммы начнем с выбора контура, для которого эта диаграмма будет составляться. На наш взгляд, наиболее информативно будет построить потенциальную диаграмму для контура d-b-m-a-c-s-d

, так как в этом контуре содержатся все источники ЭДС и источники тока анализируемой цепи и при таком обходе на потенциальной диаграмме будут показаны потенциалы всех узлов анализируемой схемы. Далее произведем выбор опорного узла, потенциал которого примем за ноль. Есть смысл взять за опорный узелd , как и ранее при расчетах анализируемой цепи. Потенциал этого узла положим равным нулю, как и ранее (2.44).

Определим численные значения потенциалов узлов и точек анализируемой схемы, находящихся на пути обхода выбранного нами контура d-b-m-a-c-s-d

. Поскольку потенциал узлаd равен нулю (2.44), то потенциал узлаb определится так:

Знак «плюс» при произведении означает, что потенциал узла b

повышается при переходе от узлаd анализируемой схемы к узлуb (см. полярность падения напряжения на сопротивлении от тока на схеме рис. 2.15).

Следующим определим потенциал точки m

анализируемой схемы:

Знаки при произведениях и соответствуют полярностям, показанным на схеме рис. 2.15.

Следующим за точкой m

анализируемой схемы идет узелa . Его потенциал равен:

Рис. 2.15. Эквивалентная схема анализируемой электрической цепи для построения потенциальной диаграммы

Далее определим потенциал узла c

, значение которого составит:

Потенциал точки s

, следующей за узломc по выбранному нами обходу, равен:

Обойдя таким образом весь контур d-b-m-a-c-s-d

, мы возвращаемся в узелd . При этом потенциал узлаd должен стать равным нулю. В самом деле, так оно и происходит, так как при подходе из узлаc к узлуd , потенциал последнего станет равен:

Расчет на основе баланса мощности

В ряде случаев, например, если конденсаторная установка устанавлена на трансформаторной подстанции, при определении ее мощности необходимо учитывать характеристики снабжающей энергосистемы, то есть трансформатора.

В принятых в СССР в 1974 году «Указаниях по компенсации реактивной мощности в распределительных сетях» были установлены исходные данные для определения мощности компенсирующих устройств, которые определяются предельными величинами реактивной мощности и могут быть переданы потребителю от энергосистемы в режимах наибольших и наименьших реактивных нагрузок (Б.Ю.Липкин. Электроснабжение промышленных предприятий и установок, 1981).

Мощность Q компенсирующего устройства определяется как разность между фактической наибольшей реактивной мощностью Q1 нагрузки потребителя и предельной реактивной мощностью Q2, предоставляемой предприятию энергосистемой по условиям режима ее работы:

Q = Q1 — Q2 = P (tg φ1 — tg φ2)

где P — мощность активной нагрузки потребителя, tg φ1 — фактический (естественный) тангенс угла, соответствующего коэффициенту мощности cos φ1, а tg φ2 — оптимальный (требуемый) тангенс угла, соответствующий коэффициенту мощности, установленному потртебителю условиями снабжающей энергосистемы (трансформатора).

В рассмотренном выше примере активная мощность трансформатора составляет 2500 кВА, а его реактивная мощность (по паспортным данным) — 1900 кВА. В результате, поскольку часть реактивной мощности поставляется трансформатором, компенсации подлежит только разница реактивной мощности в 650 кВА, что более, чем в два раза меньше значения, полученного первым методом.

Перенапряжения в сетях 6(10) кВ

В России у эксплуатационного персонала предприятий электрических сетей сложилось довольно устойчивое мнение, что перенапряжения создают вакуумные выключатели, а элегазовые этого недостатка лишены. Но так ли это? Попробуем разобраться в причинах перенапряжений.

Причины возникновения перенапряжений в сетях

Начнем с простого утверждения, очевидного для любого человека, знакомого с курсом ТОЭ: любая коммутация (включение или отключение) какого-либо элемента сети (трансформатора, электродвигателя, конденсаторной батареи, воздушной или кабельной линии и т.д.) вызывает переходный процесс. Это связано с тем, что сеть является совокупностью индуктивностей и емкостей основного электротехнического оборудования, поэтому подключение или отключение некоторого элемента ведет к установлению нового режима. Переход сети от режима до коммутации к режиму после коммутации сопровождается изменениями токов в элементах и напряжений на них. Как правило, этот переход имеет вид затухающих колебаний, в процессе которых напряжение на емкостях оборудования относительно земли или между фазами может достигать величин значительно больших, чем номинальное. Это и называется перенапряжениями.
Подобный процесс объективен и не зависит от типа используемого выключателя. Например, можно показать, что при включении (пуске) высоковольтного электродвигателя возможно возникновение перенапряжений с кратностью до 3,3 относительных единиц (о.е.) по отношению к амплитуде наибольшего рабочего напряжения , что представляет опасность для его изоляции. Перенапряжения в этом случае не зависят от типа дугогасящей среды и определяются только моментом включения и разбросом замыкания контактов разных фаз. Исключить эти перенапряжения регулировкой хода контактов выключателя не представляется возможным.
При отключении выключателем любого типа (маломасляным, вакуумным, элегазовым, электромагнитным) практически каждого двойного или двухфазного замыкания на землю в сети 6-10 кВ с изолированной или заземленной через дугогасящий реактор нейтралью на все присоединения, включенные на данную секцию, воздействуют перенапряжения с кратностью до 3,4 о.е. Причиной их является неодновременное отключение тока в поврежденных фазах, когда на первой отключившейся фазе напряжение восстанавливается от нуля до амплитуды линейного. При этом в процессе колебаний напряжение достигает величины двойного линейного. Именно эти перенапряжения могут вызывать многоместные повреждения изоляции (и такие случаи известны в эксплуатации), когда из строя выходят сразу несколько высоковольтных электродвигателей или кабелей. И дело тут не в типе дугогасящей среды, используемой в выключателе, а в объективно существующих явлениях.
Теперь рассмотрим проблему перенапряжений при использовании вакуумных и элегазовых выключателей с учетом особенностей дугогасящей среды и конструкций этих аппаратов, а также нагрузок, ими коммутируемых.
При включениях нагрузки (трансформатора, электродвигателя, конденсаторной батареи) правильно спроектированным выключателем (не дающим отскоков контактов) его дугогасящая среда с точки зрения возникновения перенапряжений не играет никакой роли. Перенапряжения в этом случае обусловлены особенностями сети и коммутируемого присоединения как многоконтурных индуктивно-емкостных схем, моментом включения по времени и разбросом в замыкании контактов разных фаз вы-ключателя (см. выше).

Основными причинами перенапряжений на изоляции отдельного присоединения (и только его, а не всей сети) при отключении нагрузки, связанными с особенностями дугогасящей среды и конструкцией выключателя, являются срез тока и эскалация напряжения. Рассмотрим эти явления по порядку.

Вакуумный выключатель ВБСК-10,
ОАО «Электрокомплекс», г.МинусинскВакуумный выключатель 3AH5 Siemens,
ССК «Уралинвестэнерго», г.ЕкатеринбургВакуумный выключатель ВБЭ-10-20/1600 УХЛ2,
ГНПП «Контакт», г. Саратов
Элегазовый выключатель HD-4,
АBB

Срез тока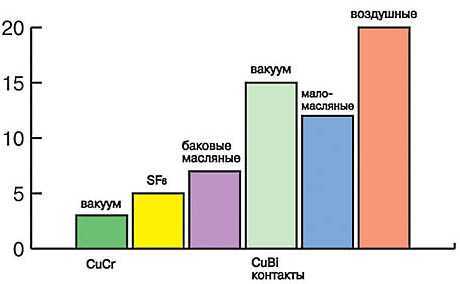
Рис.1
Относительные токи среза выключателей с разными дугогасящими средамиЭскалация напряжения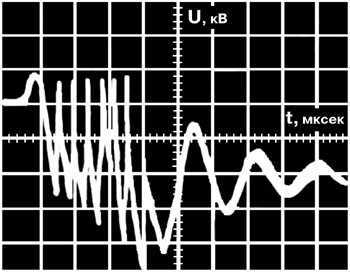
Рис.2. Экспериментальная осциллограмма отключения пускового тока электродвигателя 6,3 кВ, 736 кВт, подключенного кабелем сечением 3х95, длиной 70 м, вакуумным выключателем с возникновением эскалации напряжения с кратностью 4,0 о.е. в первой отключаемой фазе выключателя .
Масштаб: 100 мксек,
5 кВ.Литература

§ 75. Коэффициент мощности («косинус фи»)

Коэффициентом мощности, или «косинусом фи» (cos φ), цепи называется отношение активной мощности к полной мощности.

Коэффициент мощности =	активная мощность

полная мощность

или

cos φ = P/_S = P/_UI = P/_{√(P2 + Q2)}.

В общем случае активная мощность меньше полной мощности, т. е. у этой дроби числитель меньше знаменателя, и поэтому коэффициент мощности меньше единицы.

Только в случае чисто активной нагрузки, когда вся мощность является активной, числитель и знаменатель этой дроби равны между собой, и поэтому коэффициент мощности равен единице.

Чем большую часть полной мощности составляет активная мощность, тем меньше числитель отличается от знаменателя дроби и тем ближе коэффициент мощности к единице.

Величину cos φ можно косвенно определить по показаниям ваттметра, вольтметра и амперметра:

cos φ = P/_UI.

Коэффициент мощности можно также измерить особым прибором — фазометром.

Пример 14. Амперметр показывает ток 10 а, вольтметр — 120 в, ваттметр — 1 квт. Определить cos φ потребителя:

S = IU = 10 ⋅ 120 = 1200 ва,

cos φ = P/_S = 1000/₁₂₀₀ = 0,83.

Пример 15. Определить активную мощность, отдаваемую генератором однофазного переменного тока в сеть, если вольтметр на щите генератора показывает 220 в, амперметр — 20 а и фазометр — 0,8:

Р = IU cos φ = 20 ⋅ 220 ⋅ 0,8 = 3520 вт = 3,52 квт.

Полная мощность

S = IU = 20 ⋅ 220 = 4400 ва = 4,4 ква.

Пример 16. Вольтметр, установленный на щитке электродвигателя, показывает 120 в, амперметр — 450 а, ваттметр — 50 квт. Определить z, r, x_L, S, cos φ, Q:

z = U/_I = 120/₄₅₀ = 0,267 ом.

Так как Р = I2 ⋅ r, то

r = Р/_I2 = 50000/₄₅₀₂ = 0/247 ом;

x_L = √(z2 — r2) = √(0,2672 — 0,2472) = √0,01 = 0,1 ом;

S = IU = 450 ⋅ 120 = 54000 ва = 54 ква;

cos φ = Р/_S = 50000/₅₄₀₀₀ = 0,927;

Q = √(S2 — Р2) = √(540002 — 500002) = √416000000 = 20396 вар = 20,396 квар.

Из построения треугольников сопротивлений, напряжений и мощностей для определенной цепи видно, что эти треугольники подобны один другому, так как их стороны пропорциональны. Из каждого треугольника можно найти «косинус фи» цепи, как показано на рис. 168. Этим можно воспользоваться для решения самых разнообразных задач.

Рис. 168. Определение коэффициента мощности из треугольников сопротивлений (а), напряжений (б) и мощностей (в)

Пример 17. Определить z, x_L, U, U_а, U_L, S, Р, Q, если I = 6 а, r = 3 ом, cos φ = 0,8 и ток отстает по фазе от напряжения.

Из треугольника сопротивлений известно, что

cos φ = r/_z,

отсюда

z = r/_{cos φ} = 3/_0,8 = 3,75 ом;

U = I ⋅ z = 6 ⋅ 3,75 = 22,5 в;

x_L = √(z2 — r2) = √(3,752 — 32) = √(14,06 — 9) = √5,06 = 2,24 ом;

U_а = Ir = 6 ⋅ 3 = 18 в;

U_L = Ix_L = 6 ⋅ 2,24 = 13,45 в;

S = IU = 6 ⋅ 22,5 = 135 ва,

или

P = I2r = 36 ⋅ 3 = 108 вт;

Р = IU cos φ = 6 ⋅ 22,5 ⋅ 0,8 = 108 вт;

Q = IU_L = 6 ⋅ 13,45 = 81 вар,

или

Q = √(S2 — P2) = √(1352 — 1082) = √6561 = 81 вар,

или

Q = I2x_L = 62 ⋅ 2,24 = 81 вар.

Основными потребителями электрической энергии являются электрические двигатели, машины и электронагревательные устройства. Все они потребляют активную мощность, которую преобразуют в механическую работу и тепло. Электрические двигатели потребляют также реактивную мощность. Последняя, как известно, совершает колебательное движение от источника к двигателю и обратно.

У ламп и электрических печей сопротивления S = Р и cos φ = 1. У электрических двигателей S = √(P2 + Q2) и cos φ меньше 1.

При неизменной передаваемой активной мощности Р величина нагрузочного тока обратно пропорциональна значению cos φ:

I = P/_U⋅cosφ

Это означает, что при тех же значениях активной мощности Р и напряжения U нагрузочный ток электрических двигателей больше, чем у электрических ламп. Если, например, коэффициент мощности электрического двигателя равен 0,5, то он потребляет в 2 раза больший ток, чем электрическая печь сопротивления той же мощности Р.

Потери мощности на нагрев проводов линии пропорциональны квадрату тока (ΔР = I2r).

Таким образом, при cos φ = 0,5 потери мощности в линии, по которой энергия передается потребителям, больше в 4 раза, чем при cos φ = 1. Кроме того, генераторы и трансформаторы будут загружены током в 2 раза больше и в этом случае требуется примерно в 2 раза большее сечение проводов для обмоток.

Отсюда видно, какое важное значение имеет величина cos φ в электроэнергетических установках. Для повышения коэффициента мощности промышленных установок, на которых преобладающая часть потребителей — электрические двигатели, параллельно им включают конденсаторы, т. е

добиваются резонанса токов, при котором cos φ близок к 1.

е. добиваются резонанса токов, при котором cos φ близок к 1.

Электрическая емкость. Конденсатор

Электрическое поле. Напряженность электрического поля

Всякое взаимодействие между зарядами, называемое также кулоновским взаимодействием (по названию закона Кулона) происходит при помощи электростатического поля, которое является неизменяющимся по времени электрическим полем неподвижных зарядов. Электрическое поле является частью электромагнитного поля и создаётся оно электрическим зарядами или заряженными телами. Электрическое поле воздействует на заряды и заряженные тела независимо от того движутся ли они или находятся в состоянии покоя.

Одним из фундаментальных понятий электрического поля является его напряженность, которая определяется как отношение силы действующей на заряд в электрическом поле к величине этого заряда. Для раскрытия данного понятия необходимо ввести такое понятие как «пробный заряд».

«Пробным зарядом», называется такой заряд, который не участвует в создании электрического поля, а также имеет очень маленькую величину и поэтому своим присутствием не вызывает перераспределение зарядов в пространстве, тем самым не искажая электрическое поле создаваемое электрическим зарядами.

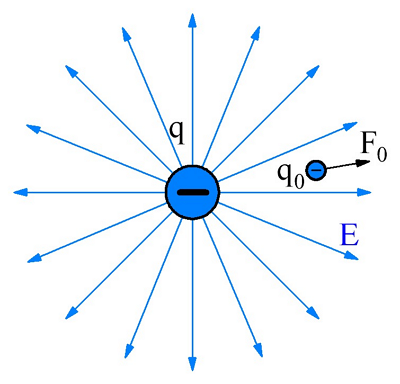
Заряд в электрическом поле.

Таким образом, если внести «пробный заряд» q в точку, находящуюся на некотором расстоянии от заряда q, то на «пробный заряд» q_П будет действовать некоторая сила F, обусловленная присутствием заряда q. Отношение силы F действующей на пробный заряд, в соответствии с законом Кулона, к величине «пробного заряда», называется напряженностью электрического поля. Напряженность электрического поля обозначается Е и имеет разрядность Н/Кл

Силовые линии

Чтобы сформировать на теоретическом уровне понятие электрического поля пользуются составлением силовых линий. Подобные линии проводятся так, чтобы направление вектора напряженности в каждой точке совпадало с направлением касательной к силовой линии. Силовые линии могут обладать рядом характерных признаков и свойств.

Они не могут пересекаться в электростатическом поле. Эти линии оказываются направленными к отрицательным зарядам от положительных зарядов.
Когда изображают силовые линии электрического поля прибегают к различной густоте из нанесения. Они должны быть соразмерны модулю вектора напряженности поля. Их густота увеличивается согласно напряженности и всегда ей пропорциональна.

В определенной точке пространства принято проводит всего одну силовую линию. Это связано с тем, что напряженность электрического поля в этой точке можно задать только однозначно.

Рисунок 2. Понятие электродинамики. Автор24 — интернет-биржа студенческих работ

Если электрическое поле однородно, тогда вектор напряженности также находится на одинаковом с ним уровне. Это проявляется во всех точках поля в пространстве. Такое поле создает плоский конденсатор-пластина. Они должны быть заряжены одинаковым количеством заряда, разделены слоем диэлектрика, однако это расстояние нужно создать меньше, чем размер самих пластин.

Электроемкость характеризует способность проводников накапливать электрический заряд в определенной точке. Она зависит от формы, взаимного расположения зарядов, размеров проводников, а также характерных свойств среды между проводниками.

Основные формулы электростатики выглядят следующим образом. Здесь представлены уравнения по взаимодействию зарядов, электрическому потенциалу, работе электростатического поля, электроемкости, а также напряженности электрического поля.

Рисунок 3. Основные формулы в электростатике. Автор24 — интернет-биржа студенческих работ

Также электродинамика изучает силовые линии электростатического поля, работу электростатического поля и эквипотенциальные поверхности. Также вводятся основы электрической цепи, законы постоянного тока, сопротивления и других определений, свойственных для этого раздела физики.

Недостатки переменного тока

При передаче энергии изменяющего направление тока на большие расстояния возникают затруднения. Создание Единой Энергетической Системы выявило ряд недостатков:

пропускная способность кабельных линий низкая из-за ёмкости между проводниками и землёй;
при объединении и кольцевании ветвей системы, расположенных друг от друга на больших расстояниях, невозможно выполнить синхронизацию станций;
пороговый предел устойчивости, необходимый для согласования, заканчивается на длинах линий свыше 500 км, при этом требуется повышение напряжения до 450 кВ, что приводит к удорожанию оконечного оборудования.

К сведению. При повышенном напряжении у воздушных линий возникает коронный разряд. Это процесс ионизации у проводников с малым радиусом. Чтобы в этом случае не происходило стекание электричества, приходится увеличивать диаметр проводов, это ведёт к удорожанию линии.