Основные логические операции
Существует три основных логических операции при помощи которых можно записать любое логическое выражение (не пугайтесь)
1. Инверсия2. Конъюнкция3. Дизъюнкция
Конъюнкция, оно же «Логическое И», оно же «Логическое умножение».
Мы выбираем название «Логическое И» – оно чаще встречается в программировании.
Допустим, у нас есть два простых выражения – А и В. Эти выражения могут иметь значения или 1 (истина), или 0 (ложь). При выполнении операции «Логическое И» мы получим сложное выражение которое примет значение 1 (истина) только в том случае если и А, и В имеют значение 1 (истина), во всех других случаях результат будет 0 (ложь).
Операция «Логическое И» имеет обозначения (в языках программирования): И, &&, AND, &.
Дизъюнкция, оно же «Логическое ИЛИ», оно же «Логическое сложение».
Мы выбираем название «Логическое ИЛИ». Кстати, если логически подумать, то можно и догадаться какие результаты будут при выполнении этой операции.
В «Логическом И» результат равен 1, если и А, и В, равны 1, а в «Логическом ИЛИ» результат будет равен 1, если или А, или В, равны единице.
Операция «Логическое ИЛИ» имеет обозначения: ИЛИ, ||, OR, |.
Инверсия, оно же «Логическое НЕ», оно же «Отрицание».
Мы выбираем название «Логическое НЕ».
Операция «Логическое НЕ» имеет обозначения: НЕ, !, NOT.
Тут вообще все просто:
Если А=1 (истина), то после выполнения операции «Отрицание» А примет значение 0, то есть становится ложным. И наоборот.
Есть еще одно название этой операции «Инвертор», а применяется оно в отношении цифровых микросхем.
В программировании часто применяется еще одна логическая операция – симбиоз «Логического И» и «Логического ИЛИ»:Строгая дизъюнкция, оно же «Исключающее ИЛИ», оно же «Логическое сложение, исключающее ИЛИ», оно же «Сложение по модулю 2»
Мы выбираем название «Исключающее ИЛИ»
Операция «Исключающее ИЛИ» имеет обозначения: Искл.ИЛИ, XOR, ^.
В этом случае, при выполнении операции «Исключающее ИЛИ», результат будет истинен (равен 1), если А не равно В. В остальных случаях результат будет равен 0 (ложный).
Высказывание и операции над высказыванием
Исходным (базовым) понятием является простое высказывание.
Под высказыванием обычно понимают всякое предположение, утверждающее что-либо о чем-либо. Если смысл,
содержащийся в высказывании, соответствует
действительности, то высказывание является истинным, иначе
ложным.
Обычно элементарные высказывания обозначают строчными буквами латинского алфавита $a$, $b$, $c$,
$x$, $y$ …, которые являются логическими переменными в логических формулах. Истинные
значения обозначаются
буквой И (True, T) или 1, а ложные – Л (False, F) или 0.
Бинарные функции
$n = 2$ — количество аргументов.
$k_n = 2^2 = 4$
$k_ф = 2^4 = 16$
| $x$ | $y$ | $f_0$ | $f_1$ | $f_2$ | $f_3$ | $f_4$ | $f_5$ | $f_6$ | $f_7$ | $f_8$ | $f_9$ | $f_{10}$ | $f_{11}$ | $f_{12}$ | $f_{13}$ | $f_{14}$ | $f_{15}$ |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
| const «0» | $x \land y$ | пер. $x$ | пер. $y$ | $x \xor y$ | $x \lor y$ | const «1» |
Номер функции совпадает с двоичной записью функции
- $f_1$ — коньюнкция. $x \& y$ — $x$ и $y$ — ${x} and {y}$ $x \&\& y$
- $f_7$ — дизъюнкция. $x | y$ — $x$ или $y$
- $f_{11}$ и $f_{13}$ — импликация (следование)
- $f_9$ — равнозначность, эквивалентность, равносильность. ${x} \equiv {y}$
- $f_6$ — равнозначность, эквивалентность, равносильность. ${x} \equiv {y}$
Из элементарных высказываний можно составить более сложные с помощью логических связок:
- $\lnot$ — логическое «не» (отрицание)
- $\land$ — логическое «и» (конъюнкция) — «и одновременно»
- $\lor$ — логическое «или» (дизъюнкция)
- $\Rightarrow$ — «логическое следствие» (импликация)
- $\equiv$ — «эквивалентность»
- круглых скобок (, ) — групировка операций.
- …есть и другие (менее распространённые) связки…
Логические связки
можно определить с помощью таблицы истинности. В левой части этой таблицы перечисляются
все
возможные
комбинации значений логических переменных $x$ и $y$. В правой части – соответствующие им им значения выражений из
переменных и логических связок.
| $x$ | $y$ | $\lnot x$ | $x \land y$ | $x \lor y$ | $x \Rightarrow y$ | $x \equiv y$ |
| 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 | |||
| 1 | 1 | |||||
| 1 | 1 | 1 | 1 | 1 | 1 |
Связки имеют следующий приоритет: $\lnot \land \lor \Rightarrow \equiv$ (приоритет можно изменить с помощью скобок).
Высказывания (формулы) из простых высказываний, связок и скобок, называют правильно построенными формулами
или просто формулами.
Значение логических связок близко к соответствующим высказываниям на
естественном языке. Например смысл связок $\lnot$ и $\land$ практически
совпадает со смыслом слов «не» и «и». Однако имеются и некоторые различия. Так формула
$x \lor y$ несколько шире, чем русское «$x$ или $y$».
Выражение «$x$ или $y$» по смыслу это формула $x \land \lnot y \lor \lnot x \land y$ (исключающее или). Еще больше
различий между семантикой
формулы $x \Rightarrow y$ в логике высказываний и выражению «из $x$ следует $y$». В русском языке это выражение
истинно, если истинны $x$ и $y$, т.е. предложение русского языка по смыслу совпадает с формулой $x \land y$.
Логическое следствие истинно также, если $x$ и
$y$ ложны или $x$ ложна, а $y$ истинна. Логическую формулу $x \Rightarrow y$ следует
интерпретировать на естественном языке так: «Если $x$ истинна, то $y$ тоже истинна, а остальное
неизвестно».
Таблица истинности — таблица в которой в левой части перечислены все возможные значения переменных, а в правой
части значения функции. Для построения таблицы истинности выписываются все возможные значения аргументов, а потом
поэтапно вычисляем значения.
Для любой формулы также можно написать таблицу истинности. Например:
| $x$ | $y$ | $\lnot x$ | $\lnot y \lor y$ | $\lnot x \land (\lnot y \lor y)$ | $\lnot x \land (\lnot y \lor y) \Rightarrow \lnot x$ |
| 1 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | ||||
| 1 | 1 | 1 |
Если формула содержит $n$ переменных, то в таблице истинности будет $2^n$
строк (в примере формула содержит 2 переменные и $2^2 = 4$ строки). Кроме того, данная формула истинна на
любом наборе значений своих переменных (везде 1). Такие формулы называются тождественно истинными или
тавтологиями. В противоположной ситуации, формула является тождественно ложной или
невыполнимой. Если две разные формулы принимают одинаковые значения на любом наборе значений переменных, то
такие формулы называют равносильными. Равносильные формулы обозначаются знаком равенства =.
3.11. Что такое переключательная схема
В компьютерах и других автоматических устройствах широко применяются
электрические схемы, содержащие сотни и тысячи переключательных элементов: реле,
выключателей и т.п. Разработка таких схем весьма трудоёмкое дело. Оказалось, что
здесь с успехом может быть использован аппарат алгебры логики.
|
Переключательная схема — это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал. |
Каждый переключатель имеет только два состояния: замкнутое и
разомкнутое. Переключателю Х поставим в соответствие логическую
переменную х, которая принимает значение 1 в том и только в том случае,
когда переключатель Х замкнут и схема проводит ток; если же переключатель
разомкнут, то х равен нулю.
Будем считать, что два переключателя Х и связаны
таким образом, что когда Х замкнут, то
разомкнут, и наоборот. Следовательно, если переключателю Х поставлена в
соответствие логическая переменная х, то переключателю должна
соответствовать переменная .
Всей переключательной схеме также можно поставить в соответствие логическую
переменную, равную единице, если схема проводит ток, и равную нулю — если не
проводит. Эта переменная является функцией от переменных, соответствующих всем
переключателям схемы, и называется функцией проводимости.
Найдем функции проводимости F некоторых переключательных схем:
- a)
- Схема не содержит переключателей и проводит ток всегда, следовательно
F=1; - б)
- Схема содержит один постоянно разомкнутый контакт, следовательно
F=0; - в)
- Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х
разомкнут, следовательно, F(x) = x; - г)
- Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда
х замкнут, следовательно, F(x) = ; - д)
- Схема проводит ток, когда оба переключателя замкнуты, следовательно,
F(x) = x . y; - е)
- Схема проводит ток, когда хотя бы один из переключателей замкнут,
следовательно, F(x)=x v y; - ж)
- Схема состоит из двух параллельных ветвей и описывается функцией .
|
Две схемы называются равносильными, если через одну из Из двух равносильных схем более простой считается та |
Задача нахождения среди равносильных схем наиболее простых является очень
важной. Большой вклад в ее решение внесли российские учёные Ю.И
Журавлев,
С.В. Яблонский и др.
При рассмотрении переключательных схем возникают две основные задачи:
синтез и анализ схемы.
СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим трём
этапам:
- составлению функции проводимости по таблице истинности, отражающей эти
условия; - упрощению этой функции;
- построению соответствующей схемы.
АНАЛИЗ СХЕМЫ сводится к
- определению значений её функции проводимости при всех возможных наборах
входящих в эту функцию переменных. - получению упрощённой формулы.
Примеры.
1. Построим схему, содержащую 4 переключателя
x, y, z и t, такую, чтобы она проводила ток тогда и только тогда, когда замкнут
контакт переключателя t и какой-нибудь из остальных трёх контактов.
Решение. В этом случае можно обойтись без построения таблицы
истинности. Очевидно, что функция проводимости имеет вид F(x, y, z, t) =
t . (x v y v z), а схема выглядит так:
2. Построим схему с пятью переключателями,
которая проводит ток в том и только в том случае, когда замкнуты ровно четыре из
этих переключателей.
![]()
Схема имеет вид:
3. Найдем функцию проводимости схемы:
Решение. Имеется четыре возможных пути прохождения тока при замкнутых
переключателях a, b, c, d, e : через переключатели a, b; через переключатели a,
e, d; через переключатели c, d и через переключатели c, e, b. Функция
проводимости F(a, b, c, d, e) = a . b v a .
e . d v c . d v c .
e . b.
4. Упростим переключательные схемы:
а)
Решение:
Упрощенная схема:
б)
![]() .
.
Здесь первое логическое слагаемое является
отрицанием второго логического слагаемого , а
дизъюнкция переменной с ее инверсией равна 1.
Упрощенная схема :
в)
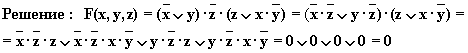
Упрощенная схема:
г)
![]()
Упрощенная схема:
д)
(по
закону склеивания)
Упрощенная схема:
е)
Решение: 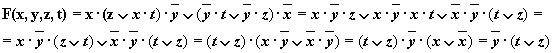
Упрощенная схема:
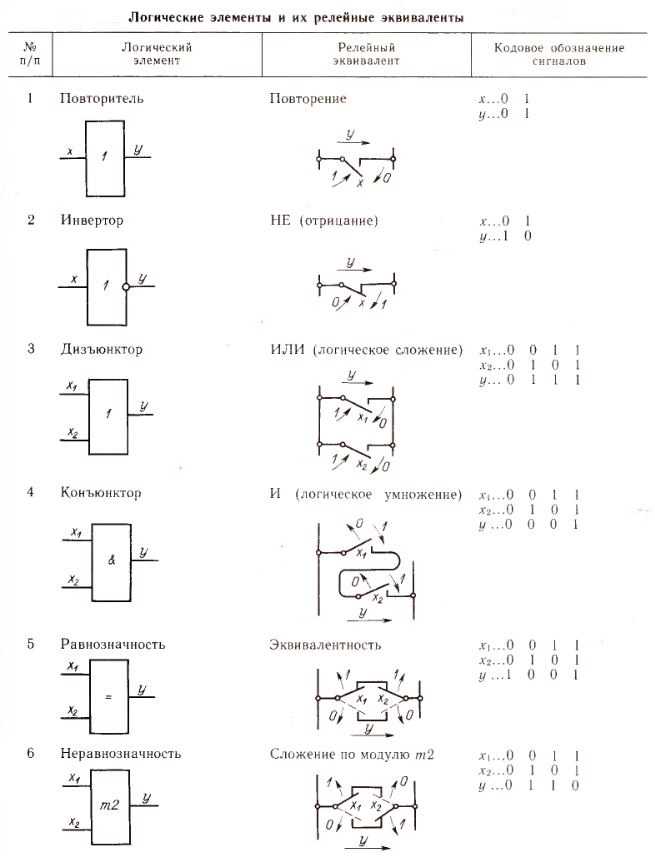
Логические элементы и их релейные эквиваленты
С помощью логических элементов довольно легко реализуются функции алгебры логики, которая является костяком устройств автоматики и вычислительных машин. Логические элементы могут реализовываться огромным количеством способов в зависимости от надобности и состоять из полупроводниковых, релейных, интегральных, пневматических и других элементов и схем.
Между величинами, входящими и выходящими из логического элемента, существует определенная зависимость, которая называется функциональной и обозначается как y = f(x) для устройств с одной переменной и как y = f(x1, x2) для устройств с двумя переменными величинами. В этой записи Х называют независимую переменную или аргумент, а Y – зависимая переменная, так как ее значение напрямую зависит от значения аргумента Х.
Ниже показана таблица логических элементов и эквивалентных им положений контактов реле:
Функция повторения
Реализуется логическим элементом повторителем (пункт 1 в таблице). Повторитель можно сравнить с нормально открытым контактом реле. При открытом контакте Х=0 и, соответственно Y=0, то есть цепь находится в непроводящем состоянии, а при закрытом наоборот Х=1 и Y=1, то есть цепь находится в проводящем состоянии.
Функция отрицания
Реализует данную функцию логический элемент НЕ или как его часто называют – инвертор (пункт 2 в таблице). Его сравнивают с нормально закрытым контактом реле, когда при отсутствии напряжения на катушке управления (Х=0) его контакт находится в проводящем состоянии (Y=1). При подаче напряжения на катушку (Х=1) контакт размыкается и разрывает цепь (Y=0).
Функция логического сложения
В схемотехнике носит название дизъюнкция или функция ИЛИ (пункт 3 в таблице). Реализуема эта функция логическим элементом дизъюнктором. Суть данной операции заключается в логическом суммировании входных сигналов X для получения результирующего сигнала на выходе Y. Описывается данная зависимость простой формулой X1 + X2 = Y. Вот примеры – 0+0=1, 1+0=1,0+1=1,1+1=1. На примере обычного реле – это два параллельно подключенных нормально разомкнутых контакта. Если один контакт разомкнут, то проводимость цепи обеспечит второй, замкнутый контакт. Для того что бы цепь оказалась разорванной, необходимо разомкнуть оба контакта.
Функция логического умножения
В схемотехнике носит название конъюнкция или функция И (пункт 4 в таблице). Реализует ее специальный логический элемент – конъюктор. Данная функция – логическое перемножение сигналов:
![]()
Если сравнить с реле – то это два последовательно включенные нормально открытые контакты. А при таком подключении контактов реле проводимость можно получить только в случае, когда оба контакта замкнуты.
Функция равнозначности
Имеет следующий вид — X1≡X2 = Y или в виде логических символов: 0≡0 =1; 1≡0 = 0; 0≡1 = 0; 1≡1 = 1.
Значения 1 будет только при условии, что X1 = X2. Эквивалентом в релейной схеме будет два последовательно включенных переключающихся контакта (пункт 5 в таблице).
Основные логические операции
Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.
Логическое отрицание (инверсия) —НЕ
Данная операция используется при обозначении отрицания. Она обозначается знаками — NO, NOT, ! В=2 (истина), а после выполнения операции отрицания, В, к примеру, приобретет значение 1 (ложное).
Таблица истинности инверсии:
Результаты операции НЕ следующие:
-
если исходное выражение истинно, то результат его отрицания будет ложным;
-
если исходное выражение ложно, то результат его отрицания будет истинным.
Логическое сложение (дизъюнкция, объединение) — ИЛИ
Понятие «Логическое ИЛИ» также можно заменить понятием «Дизъюнкция». Данная операция обозначается знаками — ИЛИ, OR, ||, |.
Но есть небольшое отличие: в «Логическом И» результат отрицания равен единице, если оба обозначения равны единице, а в «Логическом ИЛИ» итог равен единице, если одно из обозначений равно единице.
Таблица истинности операции ИЛИ:
Логическое умножение(конъюнкция) — И
В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.
За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).
При всех остальных значениях операция будет ложной.
Таблица истинности операции И приведена ниже:
Логическое следование (импликация) — ЕСЛИ ТО
Данная программа имеет также название «Импликация». Она образуется из двух высказываний, которые соединяет: «если…, то».
Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if…then.
Таблица истинности операции ЕСЛИ ТО выглядит так:
Операция эквивалентности (равнозначности) — А ТОГДА И ТОЛЬКО ТОГДА, КОГДА В
Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.
И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.
Таблица истинности операции эквивалентности:
Простой логический пробник
Схема логического пробника для отыскания неисправностей цифровых схем, описание его возможностей и приемов работы с пробником.
Общеизвестно, что для ремонта и налаживания электронных цифровых схем необходим осциллограф. Конечно, сейчас прошли те времена, когда приходилось на заводах ремонтировать большие ЭВМ.
Зато появились устройства различного назначения на микроконтроллерах, специализированных микросхемах, большое количество устройств с использованием цифровых микросхем малой степени интеграции (еще не все предприятия и организации успели приобрести современное импортное оборудование).
Обычным авометром невозможно увидеть процессы, происходящие в импульсных схемах и сделать выводы о работе схемы в целом. Но осциллограф под рукой может оказаться не всегда. Вот в этом случае может оказать неоценимую помощь описываемый логический пробник.
Подобных устройств в литературе было описано немало и все они при одинаковом назначении все-таки имеют совершенно разные параметры: есть такие, что просто неудобны и непонятны в работе. Такие пробники выпускались отечественной промышленностью до конца прошлого века.
Много лет мне довелось пользоваться логическим пробником, конструкция которого описана ниже. Схема показала себя надежной и удобной в работе.
Основное отличие данной схемы от подобных – минимальное количество деталей при достаточно широких возможностях. Одной из особенностей схемы является наличие второго входа, что иногда позволяет обходиться без двулучевого осциллографа.
- Электрическая принципиальная схема логического пробника
- Описание принципиальной схемы.
- Питание пробника (+5В) осуществляется от проверяемой схемы.
Исследуемый сигнал поступает на базы входных транзисторов VT1, VT2, предназначенных для увеличения входного сопротивления прибора. Далее, через диоды VD1, VD2 сигнал проходит на логические элементы D1.2, D1.3, D1.4, которые зажигают красный и зеленый светодиоды.
Приемы работы с пробником.
Свечение красного светодиода говорит о наличии на входе 1 логической единицы, а зеленого – логического нуля.
Для описываемого пробника напряжение логического нуля 0…0,4В, а логической единицы 2,4…5,0В. Если вход 1 пробника никуда не подключен, оба светодиода погашены.
Кроме показа логических уровней нуля и единицы пробник также может показывать наличие импульсов. Для этих целей служит двоичный счетчик D2, к выходам которого подсоединены светодиоды HL1…HL4 желтого цвета.
С приходом каждого импульса состояние счетчика увеличивается на единицу. Если частота следования импульсов невелика, то можно увидеть мигание светодиодов счетчика, даже если импульс длительностью несколько микросекунд появляется раз в секунду или еще реже. Такой процесс можно зафиксировать только с помощью запоминающего осциллографа – прибора достаточно дорогого и редкого.
Когда импульсы следуют с высокой частотой, кажется, что светодиоды HL1…HL4 светятся непрерывно, хотя на самом деле зажигаются импульсами.
Соотношение импульса и паузы может быть таким, что заметно свечение только лишь одного светодиода. Но если при этом счетчик продолжает считать, то значит идут импульсы. Для сброса счетчика используется кнопка S1: если после ее нажатия и отпускания светодиоды HL1…HL4 погасли и своего состояния не изменяют, то импульсов нет, а пробник показывает просто логический уровень нуля или единицы.
Несколько слов о деталях.
Диоды VD1, VD2 могут быть заменены любыми импульсными маломощными диодами. Только при этом следует помнить, что VD1 должен быть кремниевым, а VD2 обязательно германиевым: именно они разделяют уровень нуля и единицы. Транзисторы могут быть с любыми буквенными индексами, либо заменены на КТ3102 и КТ3107.
Микросхемы могут быть заменены импортными аналогами: К155ЛА3 на SN7400N, а К155ИЕ5 на SN7493N.
При работе с пробником необходимо внимательно следить за тем, чтобы не подключить питание к цепям с напряжением более 5В, а также не касаться таких цепей измерительным щупом. Подобные касания приводят к ремонту прибора.
Борис Аладышкин
Логический элемент «И-НЕ»
Показана схема на рис. 5 а. Здесь диод Д3 выполняет роль так сказать фильтра во избежание искажения сигнала. Если на вход х1 или х2 не подан сигнал (х1=0 или х2=0), то через диод Д1 или Д2 будет протекать ток. Падение на нем не равно нулю и может оказаться достаточным для открытия транзистора. Последствием чего может стать ложное срабатывание и на выходе вместо единицы мы получим ноль. А если в цепь включить Д3, то на нем упадет значительная часть напряжения открытого на входе диода, и на базу транзистора практически ничего не приходит. Поэтому он будет закрыт, а на выходе будет единица, что и требуется при наличии нуля на каком либо из входов. На рис. 5б и в показаны таблица истинности и схемное обозначение данного устройства.
Несмотря на простоту реализуемой логической функции способов создания инверторов немного (рис. 2.2).
Рис. 2.2. Схемы реализации инверсии на различных элементах: а
– инверторе; б
– ИЛИ-НЕ; в
– И-НЕ; г
– импликаторе; д
– равнозначности; е
– запрета; ж
– исключающее ИЛИ
Собственно инвертор и элементы ИЛИ-НЕ и И-НЕ не требуют наличия дополнительных опорных напряжений. Импликатор и элемент равнозначности нуждаются в нулевом логическом уровне, а элементы запрета и исключающее ИЛИ – в уровне единицы.
Способов реализации дизъюнкции (рис. 2.3) значительно меньше по сравнению с ранее рассмотренными заменами.
Отметим, что проще всего заменить дизъюнкторы элементами ИЛИ-НЕ и импликаторами, которые включают в себя операцию дизъюнкции в качестве одной из основных. В этом случае для замены требуется всего два элемента (рис. 2.3 б
, в
). В случае же использования элементов И-НЕ и запрета для замены дизъюнктора необходимо иметь три элемента (рис. 2.3 г
, д
).
По составу и структуре схемы конъюнкторов (рис. 2.4) похожи на схемы, показанные на рис. 2.3, только здесь операция дизъюнкции заменена на конъюнкцию, и наоборот.
Рис. 2.3. Схемы реализации дизъюнкции на различных элементах: а
– дизъюнкторе; б
– импликаторах; в
– ИЛИ-НЕ; г
– И-НЕ; д
– запрета
Рис. 2.4. Схемы реализации конъюнкции на различных элементах: а
– конъюнкторе; б
– запрета; в
– И-НЕ; г
– ИЛИ-НЕ; д
– импликаторах
Для импликаторов вариантов замены еще меньше (рис.2.5), чем для конъюнкторов. Примечательно то, что даже операция дизъюнкции в элементе ИЛИ-НЕ «не выручает», поскольку они требуются в количестве трех штук.
В схемотехнике ТТЛ очень часто используются сложные логические элементы И-ИЛИ и И-ИЛИ-НЕ, которые позволяют реализовывать логические функции, представленные в прямой и (или) инверсной дизъюнктивных нормальных формах. Показанный на рис. 2.6 а
логический элемент 2-4-2-3И — 4ИЛИ — НЕ способен производить следующую логическую операцию:
Рис. 2.5. Схемы реализации импликации на различных элементах: а
– импликаторе; б
– ИЛИ-НЕ; в
– И-НЕ; г
– запрета
Рис. 2.6. Варианты логических элементов И-ИЛИ и И-ИЛИ-НЕ: а
– 2-4-2-3И – 4ИЛИ – НЕ; б
— 2-2-2-2И – 4ИЛИ/2-2-2-2И – 4ИЛИ-НЕ с возможностью расширения по ИЛИ; в
– два четырехвходовых логических расширителя по ИЛИ
В других микросхемах, представляющих собой комбинированные элементы, используются не только расширители по ИЛИ, но и прямые и инверсные выходы одновременно (рис. 2.6 б
). Микросхемы, являющиеся расширителями по ИЛИ (рис. 2.6 в
), имеют дополнительные выходы коллектора (К) и эмиттера (Э), подключаемые к соответствующим клеммам основного элемента И-ИЛИ/И-ИЛИ-НЕ (см. рис. 2.6 б
).
Показанные на рис. 2.6 варианты не исчерпывают список логических элементов И-ИЛИ и И-ИЛИ-НЕ, выпускаемых промышленностью. Их разновидности приведены в соответствующих справочниках.
Рассмотренные элементы позволяют получать устройства различной сложности и реализовывать функции, представленные в дизъюнктивной нормальной или инвертированной форме, что согласуется с операцией минимизации по нулям.
Широко применяются эти элементы с более простыми интегральными микросхемами: инверторами, элементами И-НЕ и др.
В качестве примера рассмотрим схемы реализации функций равнозначности и неравнозначности на основе элементов И-ИЛИ-НЕ и инверторов (рис.2.7). Логика построения этих схем следует из взаимной инверсности функций равнозначности и неравнозначности.
Рис. 2.7. Схемы устройств, исключающее ИЛИ (а
) и равнозначности (б
) на основе инверторов и элементов И-ИЛИ-НЕ
Представляет интерес и вариант реализации функции равнозначности с применением элемента И-НЕ (рис. 2.8).
Рис. 2.8. Схема устройства равнозначности на основе элементов И-НЕ и И-ИЛИ-НЕ
Обоснование этой схемы следует из преобразований основной формулы равнозначности с помощью формул Моргана





























