Исследование зависимости мощности кпд источника тока

Мощность ИТ и внутреннее сопротивление

Определение и применение правил рук и буравчика

Можно собрать последовательную схему, в которую войдут гальванический двухполюсник и сопротивление нагрузки. Двухполюсник, имеющий внутренний импеданс r и ЭДС – Е, отдаёт на внешнюю нагрузку R ток I. Задача цепи – питание электричеством активной нагрузки, выполняющей полезную работу. В качестве нагрузки может быть применена лампочка или обогреватель.

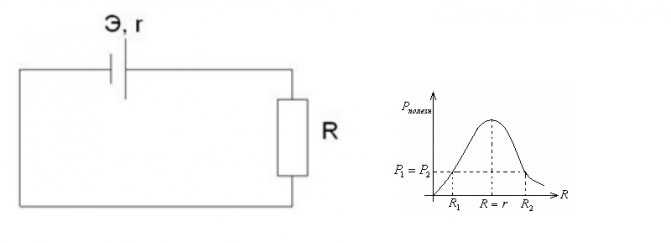
Простая схема для исследования зависимости Рполезн. от R

Рассматривая эту цепь, можно определиться с зависимостью полезной мощности от величины сопротивления. Для начала находят R-эквивалентное всей цепи.

Оно выглядит так:

Rэкв. = R + r.

Движение электричества в цепи находится по формуле:

I = E/(R + r).

В таком случае Р ЭДС на выходе составит Рвых. = E*I = E²/(R + r).

Далее можно найти Р, рассеиваемую при нагреве генератора из-за внутреннего сопротивления:

Pr = I² * r = E² * r/(R + r)².

На следующем этапе определяются с мощностью, отбираемой нагрузкой:

PR = I² * R = E² * R/(R + r)².

Общая Р на выходе двухполюсника будет равна сумме:

Рвых. = Рr + PR.

Это значит, что потери энергии изначально происходят при рассеивании на импедансе (внутреннем сопротивлении) двухполюсника.

Далее, чтобы увидеть, при какой величине нагрузки достигается максимальная величина полезной мощности Рполезн., строят график.

При его рассмотрении видно, что самое большое значение мощности – в точке, где R и r сравнялись. Это точка согласования сопротивлений генератора и нагрузки.

Внимание! Когда R > r, то ток, возникающий в цепи, мал для передачи энергии нагрузке с достаточной скоростью. При R. Наиболее наглядный пример согласования можно увидеть в радиотехнике при согласовании выходного сопротивления УНЧ (усилителя низкой частоты) и звуковых динамиков

На выходе усилителя сопротивление находится в пределах от 4 до 8 Ом, в то время как Rвх динамика составляет 8 Ом. Устройство позволяет подключить к своему выходному каскаду, как один динамик на 8 Ом, так и параллельно два по 4 Ома. И в том, и в другом случае УНЧ будет работать в заданном режиме, без потерь мощности

Наиболее наглядный пример согласования можно увидеть в радиотехнике при согласовании выходного сопротивления УНЧ (усилителя низкой частоты) и звуковых динамиков. На выходе усилителя сопротивление находится в пределах от 4 до 8 Ом, в то время как Rвх динамика составляет 8 Ом. Устройство позволяет подключить к своему выходному каскаду, как один динамик на 8 Ом, так и параллельно два по 4 Ома. И в том, и в другом случае УНЧ будет работать в заданном режиме, без потерь мощности.

В процессе разработок тех или иных реальных источников тока пользуются представлением его в виде эквивалентного блока. В его состав входят два компонента, с которыми ведётся работа: это идеальный источник и его импеданс.

Расчет коэффициента увлажнения

Указанное количество осадков, которое также выражается в миллиметрах, зависит от , температуры в данном регионе в конкретный период времени и других факторов. Поэтому несмотря на кажущуюся простоту приведенной формулы, расчет коэффициента увлажнения требует проведения большого количества предварительных измерений при помощи точных приборов и может быть осуществлен только силами достаточно крупного коллектива метеорологов.

В свою очередь, значение коэффициента увлажнения на конкретной территории, учитывающее все эти показатели, как правило, позволяет с высокой степенью достоверности определить, какой тип растительности является преобладающим в этом регионе. Так, если коэффициент увлажнения превышает 1, это говорит о высоком уровне влажности на данной территории, что влечет за собой преобладание таких типов растительности как тайга, тундра или лесотундра.

Достаточный уровень влажности соответствует коэффициенту увлажнения, равному 1, и, как правило, характеризуется преобладанием смешанных или . Коэффициент увлажнения в пределах от 0,6 до 1 характерен для лесостепных массивов, от 0,3 до 0,6 — для степей, от 0,1 до 0,3 — для полупустынных территорий, а от 0 до 0,1 — для пустынь.

Увлажнение, коэффициенты увлажнения

Коэффицие́нт поле́зного де́йствия
(КПД
) — характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии , полученному системой; обозначается обычно η («эта») . η = Wпол/Wcyм. КПД является безразмерной величиной и часто измеряется в процентах . Математически определение КПД может быть записано в виде:

X 100 %,

где А
— полезная работа, а Q
— затраченная энергия.

В силу закона сохранения энергии КПД всегда меньше единицы или равен ей, то есть невозможно получить полезной работы больше, чем затрачено энергии.

КПД теплово́го дви́гателя
— отношение совершённой полезной работы двигателя , к энергии, полученной от нагревателя. КПД теплового двигателя может быть вычислен по следующей формуле

где — количество теплоты , полученное от нагревателя, — количество теплоты, отданное холодильнику. Наибольшим КПД среди циклических машин, оперирующих при заданных температурах горячего источника T
1 и холодного T
2 , обладают тепловые двигатели, работающие по циклу Карно ; этот предельный КПД равен

Не все показатели, характеризующие эффективность энергетических процессов, соответствуют вышеприведённому описанию. Даже если они традиционно или ошибочно называются «коэффициент полезного действия», они могут иметь другие свойства, в частности, превышать 100 %.

КПД котлов

Основная статья: Тепловой баланс котла

КПД котлов на органическом топливе традиционно рассчитывается по низшей теплоте сгорания ; при этом предполагается, что влага продуктов сгорания покидает котёл в виде перегретого пара . В конденсационных котлах эта влага конденсируется, теплота конденсации полезно используется. При расчёте КПД по низшей теплоте сгорания он в итоге может получиться больше единицы. В данном случае корректнее было бы считать его по высшей теплоте сгорания , учитывающей теплоту конденсации пара; однако при этом показатели такого котла трудно сравнивать с данными о других установках.

Тепловые насосы и холодильные машины

Достоинством тепловых насосов как нагревательной техники является возможность иногда получать больше теплоты, чем расходуется энергии на их работу; аналогичным образом холодильная машина может отвести от охлаждаемого конца больше теплоты, чем затрачивается на организацию процесса.

Эффективность таких тепловых машин характеризуют холодильный коэффициент
(для холодильных машин) или коэффициент трансформации
(для тепловых насосов)

где — тепло, отбираемое от холодного конца (в холодильных машинах) или передаваемое к горячему (в тепловых насосах); — затрачиваемая на этот процесс работа (или электроэнергия). Наилучшими показателями производительности для таких машин обладает обратный цикл Карно: в нём холодильный коэффициент

где , — температуры горячего и холодного концов, . Данная величина, очевидно, может быть сколь угодно велика; хотя практически к ней трудно приблизиться, холодильный коэффициент всё же может превосходить единицу. Это не противоречит первому началу термодинамики , поскольку, кроме принимаемой в расчёт энергии A
(напр. электрической), в тепло Q
идёт и энергия, отбираемая от холодного источника.

Примеры решения задач

ПРИМЕР 1

Задание

Какова мощность механизма, который поднимает n раз в секунду молот, имеющий массу m на высоту h, если КПД машины равен ?

Решение

Мощность (N) можно найти исходя из ее определения как:

Так как в условии задана частота () (молот поднимается n раз в секунду), то время найдем как:

Работа будет найдена как:
В таком случае (принимая во внимание (1.2) и (1.3)) выражение (1.1) преобразуется к виду:
Так как КПД системы равен , то запишем:
где — искомая мощность, тогда:

Ответ

ПРИМЕР 2

Задание	Каким будет КПД наклонной плоскости, если ее длина , высота h? Коэффициент трения при движении тела о данную плоскость равен .
Решение	Сделаем рисунок. В качестве основы для решения задачи примем формулу для вычисления КПД в виде: Полезной работой будет работа по подъему груза на высоту h: Произведенную работу, при доставке груза путем перемещения его по данной плоскости можно найти как: где — сила тяги, которую найдем из второго закона Ньютона, рассмотрев силы, которые приложены к телу (рис.1):

Коэффициент полезного действия (КПД)
— это характеристика результативности системы в отношении преобразования или передачи энергии, который определяется отношением полезно использованной энергии к суммарной энергии, полученной системой.

КПД
— величина безразмерная, обычно ее выражают в процентах:

Коэффициент полезного действия (КПД) теплового двигателя определяется по формуле: , где A = Q1Q2. КПД теплового двигателя всегда меньше 1.

Цикл Карно
— это обратимый круговой газовый процесс, который состоит из последовательно стоящих двух изотермических и двух адиабатных процессов, выполняемых с рабочим телом.

Круговой цикл, включающий в себя две изотермы и две адиабаты, соответствует максимальному КПД.

Французский инженер Сади Карно в 1824 г. вывел формулу максимального КПД идеального теплового двигателя, где рабочее тело — это идеальный газ, цикл которого состоял из двух изотерм и двух адиабат, т. е. цикл Карно. Цикл Карно — реальный рабочий цикл теплового двигателя, свершающего работу за счет теплоты, подводимой рабочему телу в изотермическом процессе.

Формула КПД цикла Карно, т. е. максимального КПД теплового двигателя имеет вид: , где T1 — абсолютная температура нагревателя, Т2 — абсолютная температура холодильника.

Тепловые двигатели
— это конструкции, в которых тепловая энергия превращается в механическую.

Тепловые двигатели многообразны как по конструкции, так и по назначению. К ним относятся паровые машины, паровые турбины, двигатели внутреннего сгорания, реактивные двигатели.

Однако, несмотря на многообразие, в принципе действия различных тепловых двигателей есть общие черты. Основные компоненты каждого теплового двигателя:

• нагреватель;
• рабочее тело;
• холодильник.

Нагреватель выделяет тепловую энергию, при этом нагревает рабочее тело, которое находится в рабочей камере двигателя. Рабочим телом может быть пар или газ.

Приняв количество теплоты, газ расширяется, т.к. его давление больше внешнего давления, и двигает поршень, производя положительную работу. При этом его давление падает, а объем увеличивается.

Если сжимать газ, проходя те же состояния, но в обратном направлении, то совершим ту же по абсолютному значению, но отрицательную работу. В итоге вся работа за цикл будет равна нулю.

Для того чтобы работа теплового двигателя была отлична от нуля, работа сжатия газа должна быть меньше работы расширения.

Чтобы работа сжатия стала меньше работы расширения, необходимо, чтобы процесс сжатия проходил при меньшей температуре, для этого рабочее тело нужно охладить, поэтому в конструкцию теплового двигателя входит холодильник. Холодильнику рабочее тело отдает при соприкосновении с ним количество теплоты.

В процессе перемещения зарядов внутри замкнутой цепи, источником тока совершается определенная работа. Она может быть полезной и полной. В первом случае источник тока перемещает заряды во внешней цепи, совершая при этом работу, а во втором случае — заряды перемещаются во всей цепи. В этом процессе большое значение имеет КПД источника тока, определяемого, как соотношение внешнего и полного сопротивления цепи. При равенстве внутреннего сопротивления источника и внешнего сопротивления нагрузки, половина всей мощности будет потеряна в самом источнике, а другая половина выделится на нагрузке. В этом случае коэффициент полезного действия составит 0,5 или 50%.

Мощность тока через конденсатор

Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :

Для мгновенной мощности получаем:

График зависимости мгновенной мощности от времени представлен на рис. 3 .

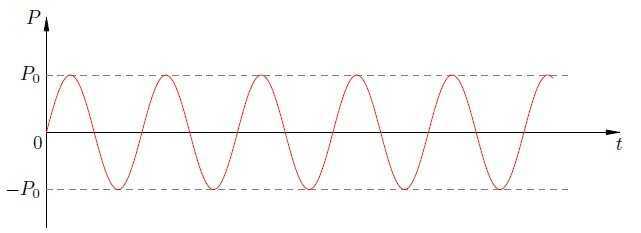
Рис. 3. Мощность переменного тока через конденсатор

Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.

Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4 ).

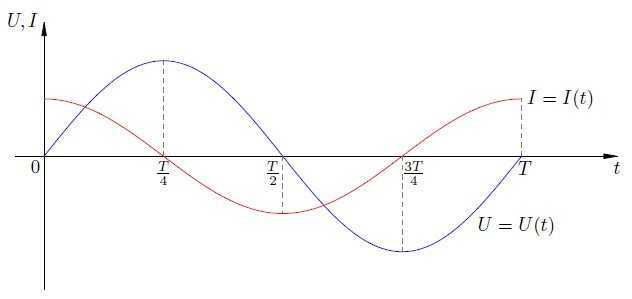
Рис. 4. Напряжение на конденсаторе и сила тока через него

Рассмотрим последовательно все четыре четверти периода.

1. Первая четверть

, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.

2. Вторая четверть

, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.

Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).

3. Третья четверть

, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.

Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.

4. Четвёртая четверть

, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.

Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.

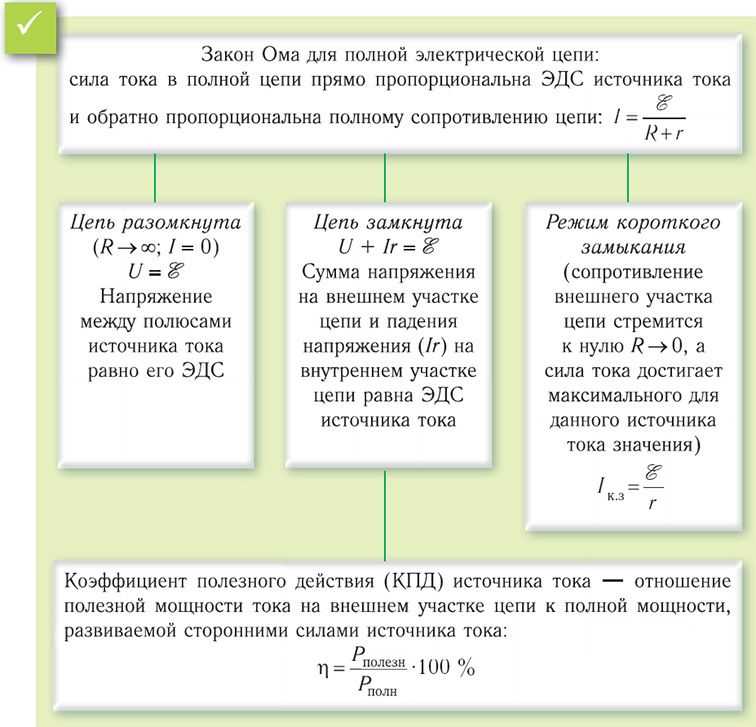
§ 26. Закон Ома для полной электрической цепи. КПД источника тока

Коэффициент полезного действия источника тока. При перемещении заряда q на внешнем участке цепи, напряжение на котором U, за промежуток времени t сила электрического поля совершает работу:

A = Uq.

Используя выражение , получим формулу для расчёта работы электрического тока, совершённой на внешнем участке

A = IUt.

В общем случае работа тока может превращаться в механическую работу А_мех электродвигателей, расходоваться на увеличение внутренней энергии участка цепи (выделение количества теплоты Q), обеспечивать увеличение химической энергии ΔE_хим , а также преобразовываться в энергию возникающего электромагнитного излучения E_изл:

IUt = A_мех + Q + ΔE_хим + E_изл.

Если к источнику тока подключён только электродвигатель, то IUt = A_мех + Q и полезной работой будет А_мех.

Если прохождение тока сопровождается химическими реакциями (например, зарядка аккумулятора), то IUt = ΔE_хим + Q и полезная работа будет равна ΔE_хим.

При работе электроосветительного оборудования IUt = E_изл + Q и полезная работа равна E_изл.

При включении в цепь только электронагревательных приборов IUt = Q и полезная работа равна Q.

При изучении физики в 8-м классе вы узнали, что, согласно экспериментально установленному закону Джоуля‒Ленца, количество теплоты, которое выделяется в проводнике при прохождении электрического тока, определяют по формуле Q = I2Rt.

Следовательно, работа тока на произвольном участке цепи в общем случае не равна количеству теплоты, выделяющемуся на этом участке при прохождении тока, т. е. IUt ≠ I2Rt.

Равенство IUt = I2Rt выполняется только в том случае, если на участке цепи имеет место превращение энергии электрического поля, поддерживаемого источником тока, во внутреннюю энергию этого участка.

Если внешним участком цепи является нагревательный элемент (или резистор), то с учётом закона Джоуля–Ленца формула для расчёта полезной работы электрического тока на внешнем участке цепи:

A_полезн = I2Rt.

Учитывая, что мощность , получим выражение для определения полезной мощности тока на тепловом потребителе, являющемся внешним участком цепи:

P_полезн = I2R = IU.

Поскольку работа сторонних сил источника тока:

A_ст = A_полн = It,

то мощность, развиваемая сторонними силами источника тока при наличии в цепи только нагревательного элемента:

P_ст = P_полн = I = IU + I2r.

Следовательно, P_полн = P_полезн + I2r.

Коэффициент полезного действия (КПД) источника тока — отношение полезной мощности тока на внешнем участке цепи к полной мощности, развиваемой сторонними силами источника тока:

Согласно формуле :

Так, например, при зарядке аккумулятора источником тока с ЭДС при силе зарядного тока I КПД этого источника определяют по формуле .

Если внешний участок цепи — нагревательный элемент, то

P_полезн = I2R,

P_полн = I2(R + r).

Тогда КПД источника тока

1. Сформулируйте закон Ома для полной цепи.

2. Как можно измерить ЭДС источника тока?

3. Какой режим работы электрической цепи соответствует короткому замыканию?

4. Что понимают под силой тока короткого замыкания?

5. Что понимают под полезной работой электрического тока? полной работой источника тока?

6. Как определить полезную мощность электрического тока? полную мощность источника тока?

7. Что называют коэффициентом полезного действия (КПД) источника тока?

Исследование мощности и КПД генератора тока

Схема стабилизатора тока на полевом транзисторе

Максимальная полезная Pmax и максимальный КПДmax – несовместимые понятия. Нельзя добиться максимального КПД источника при максимальной мощности. Это обусловлено тем, что Р, отдаваемая двухполюсником, достигнет своего максимального значения только при условии согласования сопротивления нагрузки и внутреннего импеданса ИТ:

R = r.

В этом случае КПД источника будет:

η = R/ R+r = r/ r+r = 1/2, что составляет всего 50%.

Для согласования двухполюсника и нагрузки применяют электронные схемы или согласующие блоки, для того чтобы добиться максимального отбора мощности от источника.

Расчет КПД электрической цепи

После определения основных параметров можно перейти к изучению эффективности системы. Для вычисления КПД обозначение потребления электроэнергии удобно сделать по стандартным формулам.

Определить мощность можно по следующим соотношениям силы тока, напряжения, электрического сопротивления

Выполняемая работа в цепи определяется количеством перемещенных зарядов, а также скоростью данного процесса. Для объективной оценки последнего параметра измерения выполняют с учетом определенных временных интервалов (Δt). Работу и мощность можно определить следующими формулами:

• A = P * Δt;
• P = A / Δt.

Как и в классической механике, работу можно измерить в джоулях (Дж). Мощность, по стандартам СИ, указывают в ваттах (Вт). Зависимость между отмеченными единицами:

Вт = Дж/ с (для электрических цепей вольт * ампер).

Для обозначения КПД символ «η» применяют в типовых формулах. Базовое определение с учетом приведенных замечаний можно преобразовать следующим образом:

η = A / Q * 100%,

где:

• A – выполненная работа;
• Q – энергия, полученная из источника.

Как найти КПД, формула для полной цепи

Любое подключенное устройство характеризуется определенными потерями. Резистор выделяет тепло. Трансформатор тратит часть энергии на преобразование электромагнитных волн. На примере лампы накаливания показана низкая эффективность изделия. С применением КПД увеличивают объективность оценки разных систем, подключаемых потребителей, генераторов. В следующем пункте представлена технология проверки силовых агрегатов.

Что такое источник тока

Это устройство или элемент, в общем понимании – двухполюсник, у которого проходящий через него ток не зависит от величины напряжения на полюсах. Основные характеристики источника тока (ИТ):

• величина;
• внутренняя проводимость (импеданс).

Внутреннее сопротивление такого двухполюсника очень мало. У идеального источника (ИИТ) оно приближается к нулю.

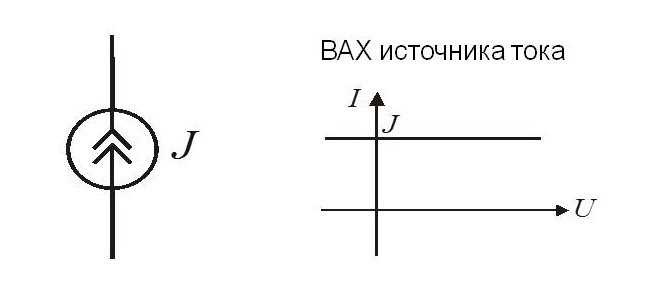
Графическое обозначение и вольт-амперная характеристика (ВАХ) ИТ

Генераторы движения электронов могут быть как независимыми, так и зависимыми.

Первые представляют собой идеальный двухполюсник, с двумя зажимами. У них ток, движущийся от одного зажима к другому, не зависит от формы и величины разности потенциалов на зажимах. Его изменения происходят по своим законам.

Второй тип ИТ – идеальный двухполюсник, с двумя зажимами, у которого движение зарядов от одного зажима к другому зависит от формы и величины напряжения на этих зажимах.

Существует управляемый зависимый ИТ. Он представляет собой идеальный двухполюсник, имеющий 2 зажима на входе и 2 зажима на выходе. Его особенность в том, что выходное значение тока на выходе зависит от его величины на входе. В таком ИТ происходит усиление мощности. Изменяя нулевое значение мощности на его входе, управляют величину мощности на выходных зажимах.

Информация. Управление производителем энергии может осуществляться напряжением (ИТУН) или током (ИТУТ). Одни находят применение для полевых триодов и электровакуумных ламп, вторые – для транзисторов биполярного типа.

В реальности генераторы тока имеют определённые ограничения по напряжению. Они далеки от идеальных ИТ и создают движение электричества в таком интервале напряжений, где их верхняя граница зависит от Uпит ИТ. Следовательно, у реального источника тока есть существенные пределы по нагрузке.

Коэффициент полезного действия (КПД)

Коэффициент полезного действия… Очень интересное название.

• «Коэффициент» – значит, какое-то число.
• «Полезного действия» – значит, есть некоторое действие и оно «полезно» для кого-то; тогда, по-видимому, существует также и «неполезное» действие.

Рассмотрим КПД сначала на бытовом примере. Допустим, вы хотите купить грецких орехов. Так получилось, что вы купили 505050 орехов. Когда вы начали их колоть и есть – оказалось, что 202020 из этих грецких орехов – пустые. «Полезными» (нужными) оказались только 303030 орехов из 505050. Тогда «эффективность» (коэффициент полезного действия) для вашей покупки грецких орехов можно подсчитать как

η=30 орехов50 орехов=35=0,6=60%eta = frac{30 ext{ орехов}}{50 ext{ орехов}} = frac{3}{5} = 0,6 = 60 \%η=50 орехов30 орехов​=53​=0,6=60%.

Аналогично «устроен» КПД в механике. КПД фактически показывает долю полезной работы от общей совершенной работы:

Например, вы равномерно затаскиваете груз по наклонной плоскости. Тащите равномерно. Тогда работа вашей силы «тратится» на увеличение потенциальной энергии и на противодействие работе силы трения:

A=∣Fтр.⋅S∣+mghA = |F_{тр.} cdot S| + mghA=∣Fтр.​⋅S∣+mgh.

Пояснение – вывод формулы A=∣Fтр.⋅S∣+mghA = |F_{тр.} cdot S| + mghA=∣Fтр.​⋅S∣+mgh

Формулу A=∣Fтр.⋅S∣+mghA = |F_{тр.} cdot S| + mghA=∣Fтр.​⋅S∣+mgh можно получить, если использовать закон сохранения энергии в присутствии внешних сил. Вспомним, что работа внешних сил равна изменению полной механической энергии:

Aвнешних сил=Eполная мех. 2−Eполная мех. 1A_ ext{внешних сил} = E_ ext{полная мех. 2} — E_ ext{полная мех. 1}Aвнешних сил​=Eполная мех. 2​−Eполная мех. 1​.

Aвнешних сил=Aтянущая наверх сила+Aсила тр.A_ ext{внешних сил} = A_ ext{тянущая наверх сила} + A_ ext{сила тр.}Aвнешних сил​=Aтянущая наверх сила​+Aсила тр.​.

При этом полная механическая энергия меняется только за счёт увеличения потенциальной энергии (скорость остаётся постоянной, кинетическая энергия никак не меняется – а потому никак не фигурирует в законе сохранения):

Eполная мех. 2−Eполная мех. 1=mgh−0E_ ext{полная мех. 2} — E_ ext{полная мех. 1} = mgh — 0Eполная мех. 2​−Eполная мех. 1​=mgh−0.

Тогда можно записать:

Тогда – с учётом работы силы трения – можно переписать наше исходное равенство:

Aтянущая наверх сила−Fтр.⋅S=mgh−0A_ ext{тянущая наверх сила} — F_{тр.} cdot S = mgh — 0Aтянущая наверх сила​−Fтр.​⋅S=mgh−0.

Или:

Aтянущая наверх сила=Fтр.⋅S+mghA_ ext{тянущая наверх сила} = F_{тр.} cdot S + mghAтянущая наверх сила​=Fтр.​⋅S+mgh.

Дополнительно для красоты можно «накинуть» на выражение для работы силы трения модуль – тогда всё точно будет положительно:

Полезным для вас является только «затаскивание» груза на высоту hhh – повышение потенциальной энергии груза. Тогда КПД в этом случае можно записать как

η=Aполез.Aзатр.⋅100%=mgh∣Fтр.⋅S∣+mgh⋅100%eta = frac{A_{полез.}}{A_{затр.}} cdot 100 \% = frac{mgh}{|F_{тр.} cdot S| + mgh} cdot 100 \%η=Aзатр.​Aполез.​​⋅100%=∣Fтр.​⋅S∣+mghmgh​⋅100%.​

Обратите внимание, что у КПД есть некоторое максимальное значение. Разберем задачу. Разберем задачу

Разберем задачу.

Условие

Для определения КПД наклонной плоскости использовано оборудование, изображённое на рисунке. Ученик с помощью динамометра поднимает брусок с двумя грузами равномерно вдоль наклонной плоскости. Данные эксперимента, записанные учеником, приведены ниже. Чему равен КПД наклонной плоскости? Ответ выразите в процентах.

• Показания динамометра при подъёме груза, Н – 1,5
• Длина наклонной плоскости, м – 1,0
• Масса бруска с двумя грузами, кг – 0,22
• Высота наклонной плоскости, м – 0,15

Выберите номер правильного варианта ответа.

1. 10%10 \%10%
2. 22%22 \%22%
3. 45%45 \%45%
4. 100%100 \%100%

Решение

Шаг 1. Давайте вспомним формулу для КПД.

Шаг 2. Теперь определим, что для нас полезная работа.

Тогда можем записать: Aполез.=mghA_{полез.} = mghAполез.​=mgh.

Как видно – в условии задачи есть все величины: и масса, и высота поднятия.

Шаг 3. Выясним, кто или что совершал(о) полную работу: и полезную, и неполезную (то есть затраченную).

Шаг 4. Нам надо найти «затраченную» работу силы тяги. Для этого надо вспомнить формулу, по которой можно найти работу.

η=Aполез.Aзатр.⋅100%=mghF⋅l⋅100%=eta = frac{A_{полез.}}{A_{затр.}} cdot 100 \% = frac{mgh}{F cdot l} cdot 100 \% =η=Aзатр.​Aполез.​​⋅100%=F⋅lmgh​⋅100%=

• =0,22кг⋅10м/с2⋅0,15м1,5Н⋅1,0м⋅100%=22%= frac{0,22 кг cdot 10 м/с^2 cdot 0,15 м}{1,5 Н cdot 1,0 м} cdot 100 \% = 22 \%=1,5Н⋅1,0м0,22кг⋅10м/с2⋅0,15м​⋅100%=22%.
• Правильный ответ: 2) 22%22 \%22%.
• Задачи для самостоятельного решения: #кпд