Явление самоиндукции

Проводящая рамка в магнитном поле

Явление электромагнитной индукции состоит в том, что при изменении поля, пронизывающего проводящую рамку или катушку, в ней возникает электродвижущая сила (ЭДС):

Рис. 1. Электромагнитная индукция, опыт Фарадея.

Энергия используемого в этом опыте магнитного поля характеризуется магнитной индукцией. Однако, при попытке описать наблюдаемое явление выяснилось, что одной этой величины мало.

Если выписать в таблицу значения ЭДС, наводимые магнитным полем, имеющим одну и ту же плотность магнитных линий, в разных условиях, то окажется, что ЭДС, возникающая в квадратной рамке, имеет гораздо большее значение, чем ЭДС в длинной узкой рамке (при одном периметре).

Причиной этого оказался разный «охват поля» рамкой. Площадь длинной узкой рамки невелика, она «охватывает» малое «количество поля», и ЭДС в ней также мала. У квадратной рамки площадь при одинаковом периметре больше, а у круглого витка – она наибольшая, в результате рамка «охватывает» большее «количество поля», и ЭДС в такой рамке тоже получается больше.

Не менее важной оказалась ориентация рамки по отношению к направлению магнитного поля. Наибольшая ЭДС возникает, если проводящая рамка перпендикулярна линиям магнитной индукции

Если плоскость рамки параллельна этим линиям – то независимо от ее площади и силы магнитного поля ЭДС в рамке не возникнет.

… а магнетизм – электричество!

Также было установлено, что магнитное поле действует на движущийся электрический заряд (см. сила Ампера и сила Лоренца), но вот доказательств того, что магнитное поле может воздействовать на неподвижный электрический заряд, долгое время получить не удавалось, но многие предполагали – хотя бы в силу симметрии! – что такое воздействие должно существовать. Честь открыть его выпала великому англичанину Майклу Фарадею: он экспериментально установил, что на электрический заряд действует меняющееся магнитное поле, или – другими словами – меняющееся магнитное поле порождает электрическое поле.

Литература

1. Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C.344- 351.
2. Жилко В.В. Физика: учеб. пособие для 11-го кл. общеобразоват. учрежде-ний с рус. яз. Обучения с 12-летним сроком обучения (базовый и повышенный уровни) / В.В. Жилко, Л.Г. Маркович. — Мн.: Нар. асвета, 2008. — С. 170-182.
3. Мякишев, Г.Я. Физика: Электродинамика. 10-11 кл.: учеб. для углубленного изучения физики / Г.Я. Мякишев, А.3. Синяков, В.А. Слободсков. — М.: Дрофа, 2005. — С. 399-408, 412-414.

Что такое магнитный поток

Магнитный поток — величина, характеризующая число магнитных силовых линий поля, проходящих через замкнутый контур.

Майкл Фарадей опытным путем пришел к выводу, что при любом соприкосновении проводника и магнитных линий по проводнику проходит заряд \(\triangle Q\). Этот заряд прямо пропорционален количеству\( \triangle Ф\) пересеченных линий и обратно пропорционален сопротивлению R контура. Пересечение линий вызывается или движением проводника, или изменением поля. 
Позже, представляя замкнутый контур, в котором действует ЭДС индукции, Джеймс Клерк Максвелл подсчитывал количество силовых линий \(\triangle Ф\), пересекаемых контуром за время \(\triangle t\). Ф он при этом отождествлял с магнитным потоком сквозь всю поверхность.

В чем измеряется, обозначение и размерность

Единица измерения — вебер, сокращенно Вб. Он обозначается буквой Ф. 

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Размерность — выражение, демонстрирующее связь физической величины с другими величинами данной системы, разложение ее на сомножители из других величин.

Размерность магнитного потока — \(В \times с = кг \times м^{2} \times с^{-2} \times А^{-1}.\)

Индуктивность

Индуктивность — это способность катушки, контура или проводника с током накапливать магнитное поле. Она характеризует способность проводника сопротивляться электрическому току. Проще всего это делать с помощью катушки, потому что катушка состоит из витков, которые представляют собой контуры. Вспомните про магнитный поток и обруч под дождем — в контуре создается магнитный поток. Где поток, там и электромагнитная индукция.

Индуктивность контура зависит от его формы и размеров, от магнитных свойств окружающей среды и не зависит от силы тока в контуре.

Как работает катушка

Вокруг каждого проводника, по которому протекает ток, образуется магнитное поле. Если поместить проводник в переменное поле — в нем возникнет ток.

Магнитные поля каждого витка катушки складываются. Поэтому вокруг катушки, по которой протекает ток, возникает сильное магнитное поле. При изменении силы тока в катушке будет изменяться и магнитный поток вокруг нее.

Задачка раз

На рисунке приведен график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 15 до 20 с. Ответ выразите в мкВ.

Решение

За время от 15 до 20 с сила тока изменилась от 20 до 0 мА. Модуль ЭДС самоиндукции равен:

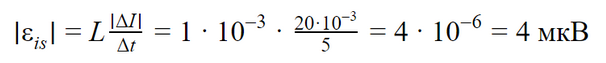
Ответ: модуль ЭДС самоиндукции с 15 до 20 секунд равен 4 мкВ.

Задачка два

По проволочной катушке протекает постоянный электрический ток силой 2 А. При этом поток вектора магнитной индукции через контур, ограниченный витками катушки, равен 4 мВб. Электрический ток какой силы должен протекать по катушке для того, чтобы поток вектора магнитной индукции через указанный контур был равен 6 мВб?

Решение

При протекании тока через катушку индуктивности возникает магнитный поток, численно равный Ф = LI.

Отсюда индуктивность катушки равна:

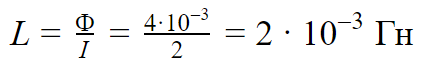
Тогда для достижения значений потока вектора магнитной индукции в 6 мВб ток будет равен:

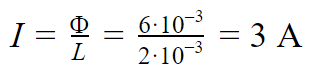
Ответ: для достижения значений потока вектора магнитной индукции в 6 мВб необходим ток в 3 А.

Опыт Ленца

Для ответа на заданные вопросы проводится следующий опыт. На концах легко вращающегося коромысла закрепляются два проводящих кольца – одно сплошное, а другое с разрезом.

Рис. 1. Опыт демонстрирующий правило Ленца.

Теперь, если взять постоянный магнит и внести его в кольцо с разрезом – ничего не произойдет. Однако, если попытаться внести постоянный магнит в сплошное кольцо – коромысло начнет вращаться, уводя кольцо от магнита.

Данное явление можно объяснить только возникновением тока в сплошном кольце. Этот ток, в свою очередь, порождает новое магнитное поле, которое и начинает взаимодействовать с полем постоянного магнита. В кольце с разрезом ток не возникает, и взаимодействующего поля нет.

Формула и правило

Наиболее изящным выражением закона электромагнитной индукции Фарадея является следующая формула:

Другими словами ЭДС в контуре есть производная магнитного потока, взятая с обратным знаком.

Представляется, однако, что для лучшего понимания явления необходимо сделать пару пояснений.

Первое: поток <mtext>Ф</mtext>\text{Ф}Ф вектора (в данном случае вектора <mover accent=»true»>B‾</mover>\overline{B}B) через поверхность – математическое понятие, это есть сумма произведений BΔScos⁡αB\Delta S\cos{\alpha}BΔScosα, где ΔS\Delta SΔS – очень маленький плоский элемент поверхности, BBB – модуль вектора в точках этого элемента, а α\alphaα – угол между нормалью к выбранному элементу и направлением вектора <mover accent=»true»>B‾</mover>\overline{B}B. Например, если поле однородно, а контур – окружность радиуса RRR, ограничивающая круг, плоскость которого перпендикулярна вектору <mover accent=»true»>B‾</mover>\overline{B}B, то поток вектора через круг <mtext>Ф</mtext>=BπR2\text{Ф} = B \pi R^2Ф=BπR2.

Второе: ЭДС, обусловленная сторонними силами, которыми в данном случае являются силы электрического поля, созданного не зарядами, а изменением магнитного поля, возбуждает в замкнутом контуре электрический ток, чье направление задается знаком минус в вышеприведенной формуле закона Фарадея. Но практически проще и физически осмысленнее (и глубже) определять его, опираясь на правило Ленца: индукционный ток производит магнитное поле, призванное компенсировать изменение потока вектора магнитной индукции исходного поля, породившее ток. К примеру, если поток индукции исходного поля уменьшается, то ток потечет таким образом, что порожденное им магнитное поле будет увеличивать поток результирующего (т.е. суммы векторов исходного и возникшего полей) вектора магнитной индукции.

Как этим пользоваться. Задача

Рассмотрим следующую задачу.

В одной плоскости расположены две квадратные рамки, изготовленные из одной и той же проволоки, причем на меньшую рамку пошло вполовину меньше провода. Сила тока, наведенная в большей рамке при изменении магнитного поля, составляет 2A2A2A. Какова сила тока, наведенная в меньшей рамке?

Дано:<mtext>п</mtext>=2\text{п}=2п=2 I=2AI=2AI=2Ai=?i = ?i=?

Решение

По закону электромагнитной индукции ЭДС в контуре E=−<mfrac>d<mtext>Ф</mtext>dt</mfrac>E = -\frac{d\text{Ф}}{dt}E=−dtdФ, <mtext>Ф</mtext>\text{Ф}Ф – поток вектора магнитной индукции через рамку. Рамки квадратные, а значит площадь меньшей из них меньше в 4 раза, как и производная потока <mtext>Ф</mtext>\text{Ф}Ф, а значит и ЭДС Е (считаем магнитное поле однородным). Ток в рамке есть отношение ЭДС к сопротивлению рамки, у меньшей рамки оно вдвое меньше, соответственно i=<mfrac>,25E,5R</mfrac>=,5I=1Ai=\frac{0,25E}{0,5R} = 0,5I = 1Ai=,5R,25E=,5I=1A.

Ответ: i=,5I=1Ai = 0,5I = 1Ai=,5I=1A.

Дифференциальная форма закона Фарадея

Магнитный поток , где  – векторная площадь над замкнутой поверхностью S. Устройство, способное поддерживать разность потенциалов, несмотря на токовые потоки, выступает источником ЭДС. В математическом виде: , где интеграл характеризуется по замкнутой петле C.

Закон Фарадея теперь можно переписать: . Используя теорему Стокса в векторном исчислении, левая часть приравнивается к

В правой части  . Поэтому мы получаем альтернативную форму закона индукции Фарадея: . Ее также именуют дифференциальной формой закона Фарадея. Это одно из четырех уравнений Максвелла, контролирующих все электромагнитные явления.

Магнитный поток, индукция и закон Фарадея	Индуцированная ЭДС и магнитный поток Закон индукции Фарадея и закон Ленца Движение ЭДС Противо-ЭДС, вихревые токи и магнитное демпфирование Изменение магнитного потока приводит к электрическому полю Электрогенераторы Электродвигатель Индуктивность Количественная интерпретация движущей ЭДС Механическая работа и электрическая энергия Энергия в магнитном поле Трансформаторы
Цепи переменного тока	Самоиндукция Схемы RL Последовательная RLC: на больших и малых частотах; Схема фазора Резисторы в цепях переменного тока Конденсаторы в цепях переменного тока: емкостное сопротивление и фазовые диаграммы Индукторы в цепях переменного тока: индуктивное сопротивление и фазовые диаграммы Резонанс в схемах RLC Мощность
Применение индукционных и электромагнитных волн	Звуковые системы, компьютерная память, сейсмограф, ВКЗЗ Антенна
Магнитные поля и прогноз Максвелла	Сохраненная энергия в  магнитном поле Прогнозы Максвелла и подтверждение Герца

Закон Фарадея-Максвелла

В 1873 Дж.К.Максвелл по-новому изложил теорию электромагнитного поля. Уравнения, которые он вывел, легли в основу современной радиотехники и электротехники. Они выражаются следующим образом:

• Edl = -dФ/dt – уравнение электродвижущей силы
• Hdl = -dN/dt – уравнение магнитодвижущей силы.

Где E – напряженность электрического поля на участке dl; H – напряженность магнитного поля на участке dl; N – поток электрической индукции, t – время.

Симметричный характер данных уравнений устанавливает связь электрических и магнитных явлений, а также магнитных с электрическими. физический смысл, которым определяются эти уравнения, можно выразить следующими положениями:

• если электрическое поле изменяется, то это изменение всегда сопровождается магнитным полем.
• если магнитное поле изменяется, то это изменение всегда сопровождается электрическим полем.

Рис. 3. Возникновение вихревого магнитного поля
Также Максвелл установил, что распространение электромагнитного поля равна скорости распространения света.

Что мы узнали?

Ученикам 11 класса необходимо знать, что электромагнитную индукцию впервые как явление обнаружил Майкл Фарадей. Он доказал, что электрическое и магнитное поле имеют общую природу. Самостоятельные исследования на основе опытов Фарадея также проводили такие великие деятели как Ленц и Максвелл, которые расширили наши познания в области электромагнитного поля.

1. /10

   Вопрос 1 из 10

ЭДС индукции

\(~E_i = -\frac {\Delta \Phi}{\Delta t},\)

где E_i – ЭДС индукции, возникающая в контуре при равномерном изменении магнитного потока (В); ΔΦ = Φ₂ — Φ₁ – изменение магнитного потока от Φ₁ до Φ₂ (Вб); Δt – время изменения магнитного потока (с); ΔΦ/Δt – скорость изменения магнитного потока (Вб/с или В).

• Эту формулу можно применять только при равномерном изменении магнитного потока.
• При увеличении магнитного потока (ΔΦ > 0), ЭДС отрицательная (ℰ_i < 0), т.е. индукционный ток имеет такое направление, что вектор магнитной индукции индукционного магнитного поля направлен против вектора магнитной индукции внешнего (изменяющегося) магнитного поля (рис. 2 а).
• При уменьшении магнитного потока (ΔΦ < 0), ЭДС положительная (E_i > 0), т.е. индукционный ток имеет такое направление, что вектор магнитной индукции индукционного магнитного поля направлен в одну и ту же сторону с вектором магнитной индукции внешнего (изменяющегося) магнитного поля (рис. 2 б).
• Знак «–» в формуле будем учитывать в задачах, где указано как изменяется (увеличивается или уменьшается) магнитный поток.

Рис. 2

Так как магнитный поток равен \(~\Phi = B \cdot S \cdot \cos \alpha\) , то он может изменяться:

• или только за счет изменения магнитной индукции поля, тогда

  
  \(~\Delta \Phi = (B_2 — B_1) \cdot S \cdot \cos \alpha\) ;
  

• или только за счет изменения площади контура, тогда

  
  \(~\Delta \Phi = B \cdot (S_2 — S_1) \cdot \cos \alpha\) ;
  

• или только за счет поворота контура в магнитном поле, тогда

  
  \(~\Delta \Phi = B \cdot S \cdot (\cos \alpha_2 — \cos \alpha_1)\) ;
  

• или одновременно за счет изменения нескольких параметров, тогда

  
  \(~\Delta \Phi = B_2 \cdot S_2 \cdot \cos \alpha_2 — B_1 \cdot S_1 \cdot \cos \alpha_1\) .
  

При любом способе изменения магнитного потока в контуре возникает ЭДС индукции.

Индукционный ток

\(~I_i = -\frac {E_i}{R},\)

где I_i – индукционный ток в контуре (А), E_i – ЭДС индукции (В), R – сопротивление контура (Ом).

План определения направления индукционного тока:

1. Установите направление вектора магнитной индукции внешнего поля (\(~\vec B\)).
2. Выясните, как изменяется (увеличивается или уменьшается) поток магнитной индукции этого поля через поверхность контура.
3. Используя правило Ленца, установите направление вектора магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) :
   • если поток магнитной индукции через контур увеличивается, то вектор магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) направлен в противоположную сторону вектора магнитной индукции внешнего поля (\(~\vec B\)) ;
   • если поток магнитной индукции через контур уменьшается, то вектор магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) направлен в ту же сторону, что и вектор магнитной индукции внешнего поля (\(~\vec B\)) .
4. Используя правило правой руки, по направлению вектора магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) найдите направление индукционного тока.

ЭДС индукции движущегося проводника

Индукционный ток в проводниках, движущихся в магнитном поле, возникает за счет действия на свободные заряды проводника силы Лоренца. Поэтому направление индукционного тока в проводнике будет совпадать с направлением составляющей силы Лоренца на этот проводник.

С учетом этого можно сформулировать следующее правило левой руки для определения направления индукционного тока в движущемся проводнике: нужно расположить левую руку так, чтобы вектор магнитной индукции входил в ладонь, четыре пальца совпадали с направлением движения проводника, тогда отставленный на 90° большой палец укажет направление индукционного тока (рис. 3).

Рис. 3

• Если проводник движется вдоль вектора магнитной индукции, то индукционного тока не будет (сила Лоренца равна нулю).
• Ток не может идти поперек проводника (заряды под действием силы Лоренца смещаются к стенкам проводника и создавать ток не будут) (рис. 4).

Рис. 4

\(~E_i = B \cdot \upsilon \cdot l \cdot \cos \alpha ,\)

где E_i – ЭДС индукции движущегося проводника (В); υ – скорость движения проводника (м/с); В – модуль вектора магнитной индукции (Тл); l – длина проводника (м); α – угол между направлением движения проводника и вектором магнитной индукции.

Магнитный поток

Прежде, чем разобраться с тем, что такое электромагнитная индукция, нужно определить такую сущность, как магнитный поток.

Представьте, что вы взяли обруч в руки и вышли на улицу в ливень. Чем сильнее ливень, тем больше через этот обруч пройдет воды — поток воды больше.

Если обруч расположен горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.

Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).

Магнитный поток по сути своей — это тот же самый поток воды через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.

Магнитным потоком через площадь ​S​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​B​, площади поверхности ​S​, пронизываемой данным потоком, и косинуса угла ​α​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Магнитный поток Ф — магнитный поток B — магнитная индукция S — площадь пронизываемой поверхности n — вектор нормали (перпендикуляр к поверхности)

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0. Это зависит от величины косинуса угла.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура, магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.