Что надо знать про электрические процессы
Если говорить простым языком, то под сопротивлением принято понимать свойство среды, по которой протекает электрический ток, снижающее его величину.
Так работают провода и изоляторы высоковольтной линии электропередач, показанные на верхней картинке, да и любое вещество.
Изоляторы обладают очень высокими диэлектрическими свойствами, изолируют высоковольтное напряжение, присутствующее на токоведущих шинах от контура земли. Это их основное назначение.
Провода же должны максимально эффективно передавать транслируемые по ним мощности. Их создают так, чтобы они обладали минимальным электрическим сопротивлением, работали с наименьшими потерями энергии на нагрев.
В этом случае передача электричества от источника напряжения к потребителю на любое расстояние будет проходить эффективно.
Приведу для примера картинку из предыдущей моей статьи.
Ее, как и верхнюю, можно представить таким обобщенным видом.
На внешнем участке цепи токоведущие жилы отделены друг от друга воздушной средой и слоем изоляции с высокими диэлектрическими свойствами.
Хорошей проводимостью обладают токоведущие жилы. Подключенный к ним электрический прибор функционирует оптимально.
Как работает резистор
Ток в металлах проходит под действием приложенного напряжения за счет направленного движения электронов. При этом они соударяются, встречаются с положительно и отрицательно заряженными ионами.
Такие столкновения повышают температуру среды, уменьшают силу тока.
За направление электрического тока в электротехнике принято движение заряженных частиц от плюса к минусу. Электроны же движутся от катода к аноду.
Электрическое сопротивление металла зависит от его структуры и геометрических размеров.
Аналогичные процессы протекают в любой другой токопроводящей среде, включая газы или жидкости.
Какие существуют виды сопротивлений
В домашних электрических приборах используется большое разнообразие резисторов с постоянной или регулируемой величиной.
Они ограничивают величину тока всех бытовых устройств, а в наиболее сложных модулях их количество может достигать тысячи или более. Резисторы работают практически во всех схемах.
При использовании в цепях переменного тока они обладают активным сопротивлением, а конденсаторы и дроссели — реактивным.
Причем, на конденсаторах создается емкостное сопротивление, а у дросселей — индуктивное.
Реактивная составляющая на конденсаторах и дросселях сильно зависит от частоты электромагнитного колебания.
2 Шутки электриков о токах через конденсатор и дроссель
Их я привожу потому, что они позволяют запомнить характер прохождения тока через реактивные элементы.
Шутка №1 о емкости
В домашней сети и внутри многих приборов работают переменный и постоянный токи. Они по-разному ведут себя, если встречают на своем пути конденсатор.
Поскольку он состоит из двух токопроводящих пластин, разделенных слоем диэлектрика, то его обозначают на схемах двумя жирными черточками, расположенными параллельно. К их серединам подключены провода, нарисованные перпендикулярными линиями.
Переменный ток имеет форму гармоничной синусоиды, состоящей из двух симметричных половинок.
Такая гармоника движется от начала координат, встречает на своем пути обкладки, переваливается через них и, скатившись, начинает обгонять приложенное напряжение.
Постоянный ток таким свойством не обладает. Его тупой конец просто упирается в обкладку и останавливается. Пройти через конденсатор он не может. Это для него непреодолимое препятствие.
Шутка №2 о дросселе
Индуктивность выполнена витками изолированного провода. Любой ток проходит по нему. Но синусоида своими волнами путается в витках катушки, начинает отставать от напряжения.
Постоянка же спокойно перемещается внутри провода дросселя без ощущения какого-либо значительного противодействия. Поэтому постоянное напряжение может своим током спалить дроссель, созданный для работы на переменке.
Что же это за зверь: сверхпроводимость
Сто лет назад выявлена способность определенных металлов полностью терять свое сопротивление электрическому току при сверхнизких температурах. Выглядит этот процесс следующим образом.
Со сверхпроводниками домашний мастер не работает
Но на верхнюю часть приведенного графика рекомендую обратить внимание: нагрев металла повышает его электрическое сопротивление
При электротехнических расчетах, требующих получения точного результата, необходимо учитывать температурный коэффициент, взятый из справочников.
Мгновенная мощность в цепи переменного тока с активным сопротивлением.
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = U m sinωt * I m sinωt = U m I m sin 2 ωt
Из тригонометрии найдём 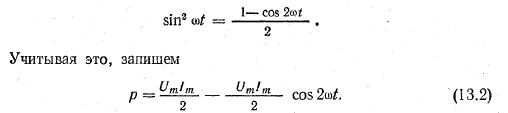
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = P m √2 = U m I m √2,то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р = UmIm√2 и перемен- ной р’:
р = Р + р’
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Емкостное сопротивление в цепи переменного тока
При включении конденсатора в цепь постоянного тока, на протяжении короткого периода времени будет наблюдаться течение по цепи зарядного тока. По окончании зарядки, когда напряжение конденсатора будет соответствовать напряжению источника тока, кратковременное течение тока в цепи прекратится. Таким образом, полностью при постоянном токе будет своеобразным разрывом цепи или сопротивлением с бесконечно большим значением. При переменном токе конденсатор будет вести себя совершенно иначе. Его зарядка в такой цепи будет осуществляться поочередно в разных направлениях. Течение переменного тока в цепи в это время не прерывается.
Более подробное рассмотрение этого процесса указывает на нулевое значение напряжения в конденсаторе в момент его включения. После поступления к нему переменного напряжения сети начнется зарядка. В это время сетевое напряжение будет возрастать на протяжении первой четверти периода. По мере того как на обкладках накапливаются заряды, происходит увеличение напряжения самого конденсатора. После того как сетевое напряжение в конце первой четверти периода станет максимальным, зарядка прекращается и значение тока в цепи станет равным нулю.
Существует формула для определения тока в цепи конденсатора: I = ∆q/∆t, где q является количеством электричества, протекающим по цепи в течение промежутка времени t. В соответствии с законами электростатики, количество электричества в устройстве составит: q = C x Uc = C x U. В этой формуле С будет емкостью конденсатора, U — напряжением сети, Uc — напряжением на обкладках элемента. В окончательном виде формула тока в цепи будет выглядеть следующим образом: i = C x (∆Uc/∆t) = C x (∆U/∆t).
При наступлении второй четверти периода произойдет уменьшение сетевого напряжения и начнется разрядка конденсатора. Ток в цепи изменит свое направление и будет течь в обратную сторону. В следующей половине периода направление сетевого напряжения изменится, наступит перезарядка элемента, а потом он вновь начнет разряжаться. Ток, присутствующий в цепи с конденсаторной емкостью, будет опережать по фазе напряжение на обкладках на 90 градусов.
Установлено что изменения тока конденсатора происходят со скоростью, находящейся в пропорциональной зависимости с угловой частотой ω. Поэтому в соответствии с уже известной формулой тока в цепи i = C x (∆U/∆t), аналогично получается, что действующее значение тока также будет представлять собой пропорцию между скоростью изменения напряжения и угловой частотой ω: I = 2π x f x C x U.
Далее уже совсем несложно установить значение емкостного сопротивления или реактивного сопротивления емкости: xc = 1/2π x f x C = 1/ ω x C. Данный параметр вычисляется, когда конденсаторная емкость включается в цепь переменного тока. Поэтому в соответствии с законом Ома в цепи переменного тока с включенным конденсатором, значение силы тока будет следующим: I = U/xc, а напряжение на обкладках составит: Uc = Ic x xc.
Часть сетевого напряжения, приходящаяся на конденсатор, получила название емкостного падения напряжения. Она известна также, как реактивная слагающая напряжения, обозначаемая символом Uc. Величина емкостного сопротивления хс, так же, как и значение индуктивного сопротивления xi напрямую связана с частотой переменного тока.
ОПРЕДЕЛЕНИЕ
Конденсатор, в простейшем случае состоит из двух металлических проводников (обкладок), которые разделяет слой диэлектрика. Каждая из обкладок конденсатора имеет свой вывод и может быть подключена к электрической цепи.
Конденсатор характеризуют при помощи ряда параметров (емкость, рабочее напряжение и т. д), одной из таких характеристик является сопротивление. Конденсатор практически не пропускает постоянный электрический ток. То есть сопротивление конденсатора является бесконечно большим для постоянного тока, но это идеальный случай. Через реальный диэлектрик очень малый ток протекать может. Этот ток называют током утечки. Ток утечки является показателем качества диэлектрика, который применяется при изготовлении конденсатора. У современных конденсаторов ток утечки составляет некоторые доли микроампера. Сопротивление конденсатора в таком случае можно вычислить, используя закон Ома для участка цепи, зная величину напряжения, до которой заряжен конденсатор и ток утечки. Но обычно при решении учебных задач сопротивление конденсатора постоянному току считают бесконечно большим.
Активное сопротивление
Активное сопротивление – это сопротивление элемента или участка цепи электрическому току, обусловленное необратимыми превращениями электрической энергии в другие формы, например, механическую в электродвигателях или тепловую, когда речь идёт о нагреве чего-либо или просто потерях или другие виды энергии. Выражается в Омах и в формулах обозначается буквой R.
Активное сопротивление характерно для проводников, а его величина зависит от свойств этих самых проводников:
- Материал — обычно проводники выполняются из металла (или из графита, как щетки электрических машин) и у каждого проводника есть удельное сопротивление, оно измеряется в Ом·мм²/м.
- Длина и площадь поперечного сечения. Следует из предыдущего. Чем больше площадь поперечного сечения (мм²) – тем меньше сопротивление, или чем длиннее проводник – тем оно больше.
- Температура. Чем больше температура – тем больше сопротивление проводника.
Согласно закону Ома, сопротивление участка электрической цепи можно рассчитать, если известны ток и напряжение по формуле: R=U/I.
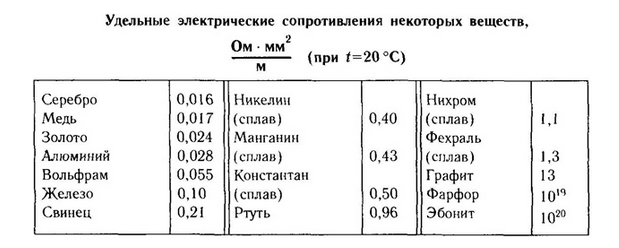
Таблица 1. Удельные электрические сопротивления некоторых веществ Таблица 1. Удельные электрические сопротивления некоторых веществ
Сопротивление проводника, определенной длины и сечения определяется по формуле: R=p*l/S,
где p (ро) – удельное сопротивление, l – длина, S – площадь поперечного сечения.
При протекании тока через активное сопротивление в любом случае происходят потери в виде тепла. По этой причине греются провода и кабельные линии под нагрузкой, трансформаторы, электродвигатели и так далее… Величина этих потерь определяется по формуле: P=U²/R. Кроме потерь в виде тепла на линии, а вернее сказать, на активном сопротивлении линии происходит падение напряжения (просадки), величина которых также рассчитывается по закону Ома: Uпад=I*Rл,
где Uпад – падение напряжение на линии, Rл – сопротивление линии.
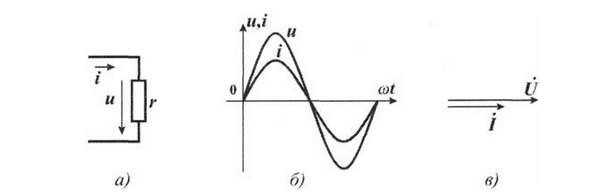
Рисунок 1 — ток и напряжение в активном сопротивлении: а) схема условного с идеальным резистором, б) Синусоиды тока и напряжения, в) векторная диаграмма. Рисунок 1 — ток и напряжение в активном сопротивлении: а) схема условного с идеальным резистором, б) Синусоиды тока и напряжения, в) векторная диаграмма.
Напряжение и ток в активном сопротивлении совпадают по фазе, соответственно коэффициент мощности у активной нагрузки в идеальном случае равен 1. Это можно пронаблюдать на иллюстрации выше, как и то, что векторы U и I также совпадают по направлению, и между ними нет угла.
Подведем итоги — активное сопротивление характерно для нагрузки ток и напряжение в которой совпадают по фазе, это могут быть: провода, резисторы, ТЭНы и другие нагревательные элементы, лампы накаливания…
Физический смысл активного сопротивления
Каждая среда, где проходят электрические заряды, создаёт на их пути препятствия (считается, что это узлы кристаллической решётки), в которые они как-бы ударяются и теряют свою энергию, которая выделяется в виде тепла.
Численную величину, характеризующую способность материала препятствовать прохождению зарядов и называют сопротивлением. Измеряется оно в Омах (Ом) и является обратно пропорциональной электропроводности величиной.
Разные элементы периодической системы Менделеева имеют различные удельные электрические сопротивления (р), например, наименьшим уд. сопротивлением обладают серебро (0,016 Ом*мм2/м), медь (0,0175 Ом*мм2/м), золото (0,023) и алюминий (0,029). Именно они применяются в промышленности в качестве основных материалов, на которых строится вся электротехника и энергетика. Диэлектрики, напротив, обладают высоким уд. сопротивлением и используются для изоляции.
Сопротивление проводящей среды может значительно изменяться в зависимости от сечения, температуры, величины и частоты тока. К тому же, разные среды обладают различными носителями зарядов (свободные электроны в металлах, ионы в электролитах, «дырки» в полупроводниках), которые являются определяющими факторами сопротивления.
Аналогия с электрическим сопротивлением проводника на примере резистора
Чтобы суметь рассчитать импеданс цепи, нужно представлять, как себя ведут различные входящие в нее элементы: катушки индуктивности, резисторные и емкостные детали, с точки зрения вклада в составляющие общей резистивности цепи.
Активное сопротивление
Резистор относится к числу пассивных деталей цепи, не содержащих внутренних источников электроэнергии, при этом почти все создаваемое им противодействие приходится на активную компоненту. Реактивная составляющая если и присутствует, то настолько мала, что ею зачастую принято пренебрегать. Это связано с тем, что отношение напряжения на деталь и электротока, проходящего через нее, не зависит от их частоты. Когда к резисторной детали присоединяют источник напряжения (обозначим его U), через нее будет идти электроток значением I. Если к концам радиодетали подсоединяют источник тока, равного I, между ними будет иметь место падение напряжения U.
Реактивное сопротивление
К основным компонентам электроцепей, несущим такую нагрузку, относятся дроссели (и подобные им индуктивные элементы) и конденсаторы. При достижении резонанса наблюдается наименьшее значение общего противодействия подключенных последовательно конденсатора и дросселя и наибольшее – включенных параллельно.
Индуктивная нагрузка
Если индуктивный дроссель подключить к постоянному току, на нем будут наблюдаться следующие эффекты: резистивность будет приближаться к нулевому значению, а при пропускании электротока через катушечный элемент падение напряжения будет отсутствовать, независимо от токовой величины:
R=U/I=0/I=0.
Такие цифры справедливы для идеального дросселя, на практике они все же несколько отклоняются от нуля. Если к детали будет приложен переменный ток, напряжение между катушечными выводами будет отличным от нуля.

Катушка индуктивности
Емкостная нагрузка
При включении идеального конденсаторного элемента в сеть с постоянным напряжением его резистивность будет иметь очень большую величину, стремящуюся к бесконечной. Когда к радиодетали прикладывают такое напряжение, проходящий через нее ток будет равен нулю. Если к выводам конденсатора подсоединить источник переменного напряжения, ток будет ненулевым.
Советуем изучить — Должностные обязанности, права и ответственность специалистов электротехнической службы

Детали, обладающие емкостью
Данные эффекты, наблюдаемые на емкостных радиодеталях и катушках, нельзя описывать в категориях активного противодействия в условиях константного электротока, так как последнее подразумевает стабильное, независимое от условий и не изменяющееся во времени отношение электротока и напряжения и исключает явление сдвига фаз между этими величинами. Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.
Важно! При рассмотрении поведения катушек и конденсаторов под действием гармонических сигналов обнаруживается, что токовая сила и напряжение могут быть связаны константной величиной, которую также называют импедансом. При ее изучении применяется понятие о гармонических сигналах, учитывающее как их амплитудные характеристики, так и особенности, связанные с фазами
Такое значение импеданса можно определить как частное комплексной амплитуды, которой обладает напряжение приложенного к двухполюсному элементу сигнала, и комплексной амплитуды идущего через элемент электротока
В отношении пассивных электроцепей со стабильными показателями в устоявшемся режиме стоит сказать, что импедансный показатель у них не будет привязанным к течению времени. Если временной параметр при формульной записи не сокращается, то категория импеданса для рассматриваемого двухполюсника окажется неприменимой
Такое значение импеданса можно определить как частное комплексной амплитуды, которой обладает напряжение приложенного к двухполюсному элементу сигнала, и комплексной амплитуды идущего через элемент электротока. В отношении пассивных электроцепей со стабильными показателями в устоявшемся режиме стоит сказать, что импедансный показатель у них не будет привязанным к течению времени. Если временной параметр при формульной записи не сокращается, то категория импеданса для рассматриваемого двухполюсника окажется неприменимой.
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Закон Ома для участка цепи.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит: Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Реактивное емкостное сопротивление — Большая Энциклопедия Нефти и Газа, статья, страница 1
Реактивное емкостное сопротивление
Реактивное емкостное сопротивление и положительное активное сопротивление элементов этой цепочки могут компенсировать связь через пространственный заряд в узком диапазоне частот. Для этого контур сигнальной сетки настраивают на частоту гетеродина и параметры компенсирующей цепи R и С подбирают так, чтобы на сигнальной сетке не появлялось заметное напряжение гетеродина.
Как и активное, реактивное емкостное сопротивление оценивают в омах. Значение его зависит от емкости и частоты: чем больше емкость и частота, тем меньше сопротивление. Катушка индуктивности, включенная в цепь переменного тока, тоже обладает реактивным сопротивлением XL: ( uL2n L. Катушка с конденсатором образует колебательный контур.
Сопротивление Хс называется реактивным емкостным сопротивлением. Оно отличается от активного сопротивления R, в котором вся мощность, отдаваемая источником тока, превращается в тепло и расходуется на нагревание сопротивления. В случае же емкостного реактивного сопротивления Хс вся работа, совершаемая источником тока при заряде конденсатора, преобразуется в энергию электрического поля, а при разряде вся энергия без остатка возвращается в источник. Потому сопротивление и называют реактивным.
нелинейным реактивным емкостным сопротивлением
При необходимости длину сварочной цепи можно нарастить, однако стабильность процесса в этом случае ухудшается ввиду увеличения активного, реактивного и емкостного сопротивления сварочной цепи и снижения возможностей источника питания по отработке возмущений, связанных с изменением вылета электрода и длины дуги. Сварочные кабели запрещено при работе укладывать в бухты или наматывать на вьюшки вследствие значительного увеличения индуктивного сопротивления сварочной цепи.
Это происходит в том случае, когда в одних ветвях преобладает реактивное индуктивное сопротивление, а в других — реактивное емкостное сопротивление.
При последовательной схеме замещения измеряемое сопротивление РК ( активная составляющая Ra) равно сумме первого и второго членов правой части выражения (3.24), третий член определяет реактивное емкостное сопротивление.
В электрических цепях переменного тока при параллельном соединении реактивных сопротивлений может возникать резонанс токов. Это происходит в том случае, когда в одних ветвях преобладает реактивное индуктивное сопротивление, а в других — реактивное емкостное сопротивление.
Практически о величине емкости конденсатора ( действующей емкости) мы судим по величине тока, потребляемого конденсатором. Наличие индуктивностиЬв конденсаторе дает увеличение его действующей емкости с ростом частоты ( рис. 30), так как ток будет возрастать за счет компенсации реактивного емкостного сопротивления индуктивным сопротивлением.
В простейшем случае резонанс напряжений может быть получен в электрической цепи переменного тока при последовательном включении катушки индуктивности и конденсаторов. При этом, изменяя емкость конденсаторов при постоянных параметрах катушки, получают резонанс напряжений при неизменных значениях напряжения и индуктивности, частоты и активного сопротивления цепи. При изменении емкости С конденсаторов происходит изменение реактивного емкостного сопротивления. При этом полное сопротивление цепи также изменяется, следовательно, изменяются ток, коэффициент мощности, напряжения на катушке индуктивности, конденсаторах и активном сопротивлении катушки и активная, реактивная и полная мощности электрической цепи.
В простейшем случае резонанс напряжений может быть получен в электрической цепи переменного тока при последовательном включении катушки индуктивности и конденсаторов. При этом, изменяя емкость конденсаторов при постоянных параметрах катушки, получают резонанс напряжений при неизменных значениях напряжения и индуктивности, частоты и активного сопротивления цепи. При изменении емкости С конденсаторов происходит изменение реактивного емкостного сопротивления. При этом полное сопротивление цепи также изменяется, следовательно, изменяются ток, коэффициент мощности, напряжения на катушке индуктивности, конденсаторах и активном сопротивлении катушки и активная, реактивная и полная мощности электрической цепи.
Страницы:
1
КПД электрической цепи
Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.
Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим .
Если сила тока в цепи равна , то
Некоторое количество теплоты выделяется также на источнике тока:
Полное количество теплоты, которое выделяется в цепи, равно:
КПД электрической цепи — это отношение полезного тепла к полному:
КПД цепи равен единице лишь в том случае, если источник тока идеальный .
Активное и реактивное сопротивление в цепи переменного тока
В электрической цепи переменного тока существует два вида сопротивлений: активное и реактивное. Это является существенным отличием от цепей постоянного тока.
Активное сопротивление
При прохождении тока через элементы, имеющие активное сопротивление, потери выделяющейся мощности необратимы. Примером может служить резистор, выделяющееся на нем тепло, обратно в электрическую энергию не превращается. Кроме резистора активным сопротивлением может обладать линии электропередач, соединительные провода, обмотки трансформатора или электродвигателя.
Отличительной чертой элементов имеющих чисто активное сопротивление – это совпадение по фазе тока и напряжения, поэтому вычислить его можно по формуле
Активное сопротивление зависит от физических параметров проводника, таких как материал, площадь сечения, длина, температура.
Реактивное сопротивление
При прохождении переменного тока через реактивные элементы возникает реактивное сопротивление. Оно обусловлено в первую очередь ёмкостями и индуктивностями.
Индуктивностью в цепи переменного тока обладает катушка индуктивности, причём в идеальном случае, активным сопротивлением её обмотки пренебрегают. Реактивное сопротивление катушки переменному току создаётся благодаря её ЭДС самоиндукции. Причем с ростом частоты тока, сопротивление также растёт.
Реактивное сопротивление катушки зависит от частоты тока и индуктивности катушки
Конденсатор обладает реактивным сопротивлением благодаря своей ёмкости. Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока.
Сопротивление конденсатора можно рассчитать по формуле
Треугольник сопротивлений
Цепи переменного тока обладают полным сопротивлением. Полное сопротивление цепи определяется как сумма квадратов активного и реактивного сопротивлений
Графическим изображением этого выражения служит треугольник сопротивлений, который можно получить в результате расчёта последовательной RLC-цепи. Выглядит он следующим образом:
На треугольнике видно, что катетами являются активное и реактивное сопротивление, а полной сопротивление гипотенуза.
Просмотров: 17913






























