Сила лоренца

Что такое сила Лоренца — определение, когда возникает, получение формулы

Известно, что электрический ток – это упорядоченное перемещение заряженных частиц. Установлено также, что во время движения в магнитном поле каждая из этих частиц подвергается действию силы. Для возникновении силы требуется, чтобы частица находилась в движении.

Сила Лоренца – это сила, которая действует на электрически заряженную частицу при её движении в магнитном поле. Её направление ортогонально плоскости, в которой лежат векторы скорости частицы и напряженности магнитного поля. Равнодействующая сил Лоренца и есть сила Ампера. Зная ее, можно вывести формулу для силы Лоренца.

Время, требуемое для прохождения частицей отрезка проводника, , где – длина отрезка, – скорость частицы. Суммарный заряд, перенесенный за это время через поперечное сечение проводника, . Подставив сюда значение времени из предыдущего равенства, имеем

                             (2)

В то же время , где – количество частиц, находящееся в рассматриваемом проводнике. При этом , где – заряд одной частицы. Подставив в формулу значение из (2), можно получить:

Таким образом,

Используя (1), предыдущее выражение можно записать как

После сокращений и переносов появляется формула для вычисления силы Лоренца

С учетом того, что формула записана для модуля силы, ее необходимо записать так:

                            (3)

Поскольку , то для вычисления модуля силы Лоренца неважно, куда направлена скорость, – по направлению силы тока или против, – и можно сказать, что – это угол, образуемый векторами скорости частицы и магнитной индукции. Запись формулы в векторном виде будет выглядеть следующим образом:

Запись формулы в векторном виде будет выглядеть следующим образом:

– это векторное произведение, результатом которого является вектор с модулем, равным .

Исходя из формулы (3), можно сделать вывод о том, что сила Лоренца является максимальной в случае перпендикулярности направлений электрического тока и магнитного поля, то есть при , и исчезать при их параллельности ().

Необходимо помнить, что для получения правильного количественного ответа – например, при решении задач, – следует пользоваться единицами системы СИ, в которой магнитная индукция измеряется в теслах (1 Тл = 1 кг·с−2·А−1), сила – в ньютонах (1 Н = 1 кг·м/с2), сила тока – в амперах, заряд в кулонах (1 Кл = 1 А·с), длина – в метрах, скорость – в м/с.

Определение направления силы Лоренца с помощью правила левой руки

Поскольку в мире макрообъектов сила Лоренца проявляется как сила Ампера, для определения ее направления можно пользоваться правилом левой руки.

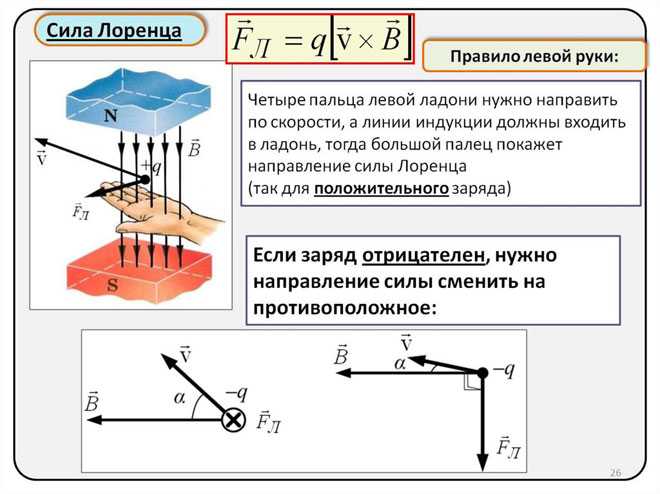
Нужно поставить левую руку так, чтобы раскрытая ладонь находилась перпендикулярно и навстречу линиям магнитного поля, четыре пальца следует вытянуть в направлении силы тока, тогда сила Лоренца будет направлена туда, куда указывает большой палец, который должен быть отогнут.

Движение заряженной частицы в магнитном поле

В простейшем случае, то есть при ортогональности векторов магнитной индукции и скорости частицы сила Лоренца, будучи перпендикулярной к вектору скорости, может менять только её направление. Величина скорости, следовательно, и энергия будут оставаться неизменными. Значит, сила Лоренца действует по аналогии с центростремительной силой в механике, и частица перемещается по окружности.

В соответствии со II законом Ньютона () можно определить радиус вращения частицы:

.

Необходимо обратить внимание, что с изменением удельного заряда частицы () меняется и радиус. При этом период вращения T = =

Он не зависит от скорости, значит, взаимное положение частиц с различными скоростями будет неизменным

При этом период вращения T = = . Он не зависит от скорости, значит, взаимное положение частиц с различными скоростями будет неизменным.

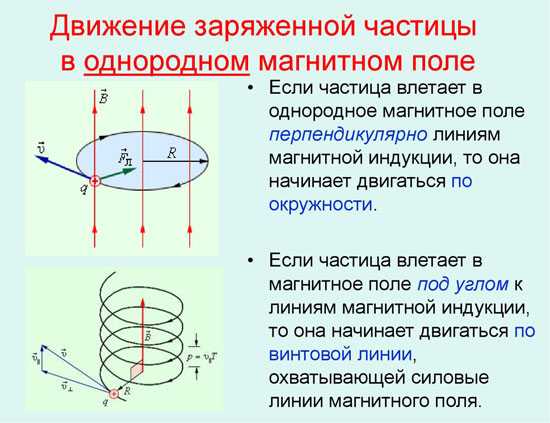
В более сложном случае, когда угол между скоростью частицы и напряженностью магнитного поля является произвольным, она будет перемещаться по винтовой траектории – поступательно за счет составляющей скорости, направленной параллельно полю, и по окружности под влиянием ее перпендикулярной составляющей.

Эффект бабочки

Это наблюдение, вкупе со многими другими открытиями, привело к подробному изучению детерминированного хаоса – иррегулярного и непредсказуемого поведения детерминистских нелинейных динамических систем (определение Родерика Дженсена из Йельского университета),явно беспорядочного, повторяющегося поведения в простой детерминистской системе, похожей на работающие часы (определение Брюса Стюарта из Брукхевенской национальной лаборатории США).

Откуда в детерминированной системе хаос и непредсказуемость? От сильной чувствительности к начальным условиям. Малейшее воздействие, от которого невозможно избавиться – округление переменной (если это теоретическая модель), ошибка измерения (если это исследование реальной системы) – и система ведет себя совершенно по-другому.

Лоренц приводил наглядный пример: если погода действительно относится к классу настолько чувствительных систем (разумеется, не все системы такие), то взмах крыльев чайки может вызвать заметные изменения погоды. Впоследствии чайка была заменена бабочкой, а в 1972 году появилась работа «Предсказуемость: может ли взмах крыльев бабочки в Бразилии вызвать торнадо в Техасе?».

Так родился знаменитый термин «эффект бабочки», отсылавший и к рассказу Брэдбери и, удивительным образом, к следующему открытию Лоренца – странному аттрактору, названному в его честь.

Главное правило

Рассмотренный нами пример является частным случаем алгоритма буравчика. Существует несколько вариантов формулировок правила, применяемых в различных ситуациях.

Общая, или главная формулировка, позволяет распространить данное правило на все случаи. Это вариант мнемонического правила, используемый для определения ориентации результирующей векторного произведения, называемого аксиальным вектором, а также для выбора связанного с этими векторами правого базиса (трёхмерной системы координат), что позволяет определить знак аксиального вектора.

Главное правило позволяет определить направление в пространстве аксиальных векторов, важных для вычислений:

• угловой скорости;
• параметров индукционного тока;
• магнитной индукции.

Хотя ориентация аксиального вектора является условной, она важна для расчётов: придерживаясь принятого алгоритма выбора, легче производить вычисления, без риска перепутать знаки.

Во многих случаях применяют специальные формулировки, хорошо описывающие частные случаи в конкретной ситуации.

Три знака после запятой

Эдвард Лоренц с детства увлекался погодой и математикой. Во время Второй мировой войны стал метеорологом ВВС США, после продолжил изучать теоретические основы метеорологии в Массачусетском технологическом институте, а также стал заниматься довольно экзотическим по тем временам делом – пытаться научиться прогнозировать погоду с помощью компьютерных моделей. Эдвард Лоренц. Фото с сайта Американского физического института.

Lenta.ru

В его распоряжении находилась вычислительная машина Royal McBee. В 1960 году Лоренц создал упрощенную модель погоды. Модель представляла собой набор чисел, описывавший значение нескольких переменных (температуры, атмосферного давления, скорости ветра) в данный момент времени. Лоренц выбрал двенадцать уравнений, описывавших связь между этими переменными. Значение переменных в следующий момент времени зависело от их значения в предыдущий момент и рассчитывалось по этим уравнениям. Таким образом, модель была полностью детерминирована.

Коллеги Лоренца от модели пришли в восторг. Машине скармливались несколько чисел, она начинала выдавать ряды чисел (впоследствии Лоренц научил ее рисовать несложные графики), описывающие погоду в некотором воображаемом мире. Числа не повторялись – они порой почти повторялись, система как будто воспроизводила старое свое состояние, но не полностью, циклов не возникало. Словом, искусственная погода была плохо предсказуема, причем характер этой непредсказуемости (апериодичность) был примерно такой же, какой и у погоды за окном. Студенты и преподаватели заключали пари, пытаясь угадать, каким будет состояние модели в следующий момент.

Зимой 1961 года Лоренц решил подробнее изучить уже построенный машиной график изменения одной из переменных. В качестве начальных данных он ввел значения переменных из середины графика и вышел отдохнуть. Машина должна была бы точно воспроизвести вторую половину графика и продолжить строить его дальше. Однако вернувшись, Лоренц обнаружил совершенно другой график. Если в начале он еще более-менее повторял первый, то к концу не имел с ним ничего общего.

Расхождение двух графиков погоды, берущих начало из одной точки. Распечатка Лоренца 1961 года, воспроизведенная в книге Джеймса Глейка «Хаос: Создание новой науки» (СПб., «Амфора», 2001).

Lenta.ru

Получалось, что модель, из которой полностью устранена случайность, при одних и тех же начальных значениях выдает совершенно разные результаты. Машина не сломалась и считала все правильно, Лоренц не опечатался при вводе данных.

Разгадка нашлась довольно быстро: в памяти машины значения переменных хранились с точностью до шести знаков после запятой (…,506217), а на распечатку выдавалось только три (…,506). Лоренц, разумеется, ввел округленные значения, резонно предположив, что такой точности вполне достаточно.

Оказалось, что нет. «…овалились маленькие костяшки домино… большие костяшки… огромные костяшки, соединенные цепью неисчислимых лет, составляющих Время», – написал в 1952 году в знаменитом рассказе «И грянул гром» Рэй Брэдбери. Примерно это же произошло в модели Лоренца. Система оказалась исключительно чувствительной к малейшим воздействиям на нее.

Динамика

К оглавлению…

Второй закон Ньютона:

Здесь: F — равнодействующая сила, которая равна сумме всех сил действующих на тело:

Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике):

Третий закон Ньютона (сила действия равна силе противодействия):

Сила упругости:

Общий коэффициент жесткости параллельно соединённых пружин:

Общий коэффициент жесткости последовательно соединённых пружин:

Сила трения скольжения (или максимальное значение силы трения покоя):

Закон всемирного тяготения:

Если рассмотреть тело на поверхности планеты и ввести следующее обозначение:

Где: g — ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести:

Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой:

Скорость спутника на круговой орбите:

Первая космическая скорость:

Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:

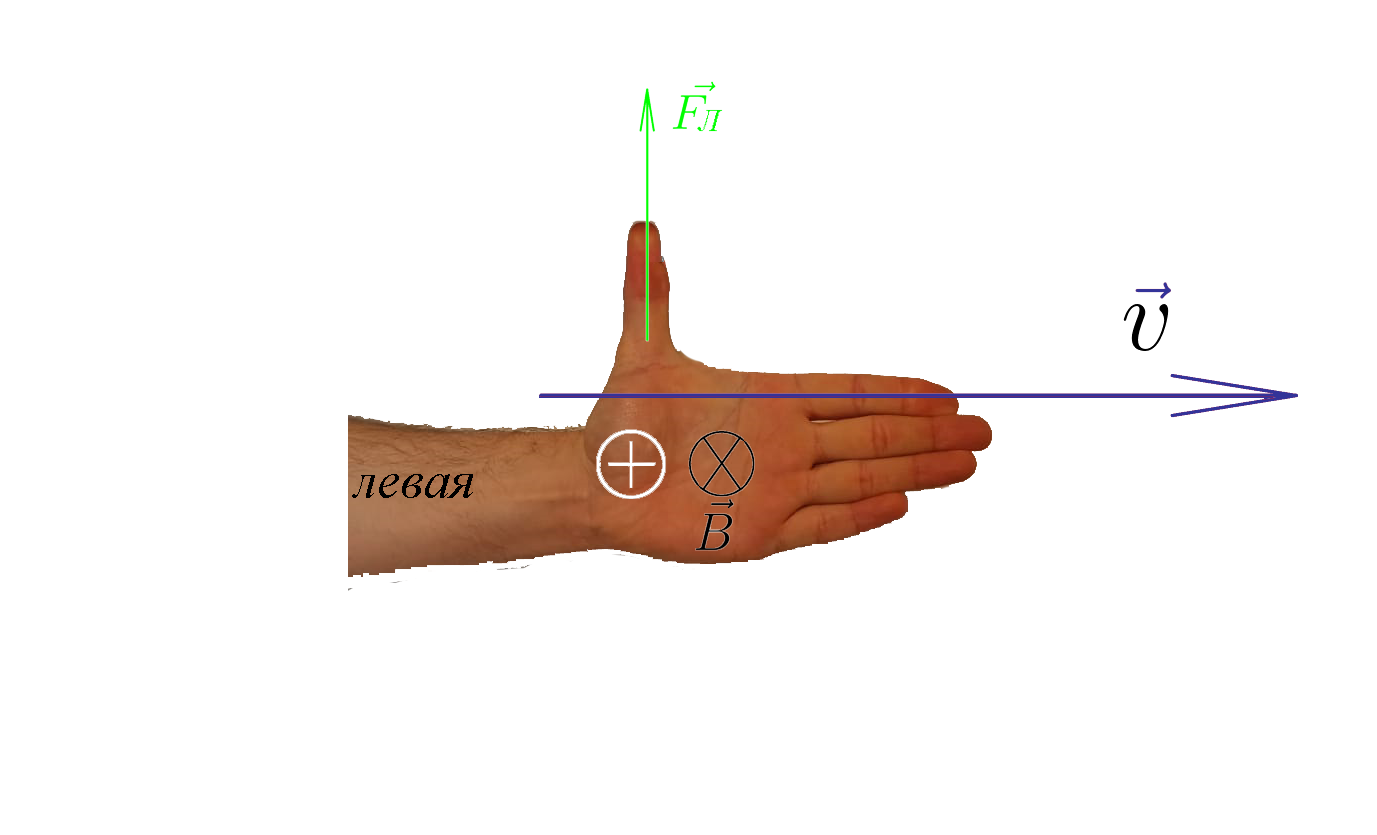
Направление силы Лоренца, действующей на положительно заряженную частицу .

Задача 1. (Сила Лоренца)
Пылинка, имеющая заряд \(q=10^{-6} \ Кл\) движется в магнитном поле с индукцией
\(B=20 \ Тл\) . Скорость пылинки перпендикулярна линиям магнитной индукции и равна

\(100 \ м/с \)

Вычислить значение силы Лоренца, действующей на пылинку со стороны магнитного поля.
Дать ответ в миллиньютонах.

Ответ: \( F_л=2 \ мН \)

Дано: \( v=100 \ м/с \) \( B=20 \ Тл \) \( q=10^{-6} \ Кл \)
\(B=20 \ Тл \) \( \alpha=90^0\)

\(F_л-?\)

\( F_л=Bqv \cdot sin \ \alpha \)

\( F_л=20 \ Тл \cdot 10^{-6} \ Кл \cdot 100 \ м/с \cdot sin \ 90^0 =2 \cdot 10^{-3} \ Н \)

\( 2 \cdot 10^{-3} \ Н = 2 \ мН \) Ответ: \( F_л=2 \ мН \)

ПОЗЖЕ

Задача 2.

Шарик с зарядом \(q=100 \ мкКл\) влетает в магнитное поле с
индукцией \(B=100 \ Тл\) со скоростью \(v=30 \ м/с .\)

Угол между вектором магнитной индукции \( \vec{B} \) и вектором скорости частицы
\( \vec{v} \) составляет \( \alpha=30^0 . \)

Найти значение силы Лоренца, действующей на шарик со стороны поля.

Ответ: \( F_л= 0,15 Н \)

Дано: \(q=100 \ мкКл \) \(B=100 \ Тл \)
\(v=30 \ м/с \) \( \alpha=30^0 \)

\(F_л-?\)

СИ

\(q=10^{-4} Кл \)

\( F_л=Bqv \cdot sin \ \alpha \)

\( F_л=100 \ Тл \cdot 10^{-4} \ Кл \cdot 30 \ м/с \cdot sin \ 30^0 =0,15 \ Н \)

Ответ: \( F_л= 0,15 Н \)

позже

Задача 3. (Сила Лоренца)

Электрон движется в магнитном поле с индукцией
\(B=1 \ Тл\) перпендикулярно линиям магнитного поля со скоростью \(v=10^8 \ м/с . \)

Вычислить значение силы Лоренца, действующей на электрон со стороны магнитного поля.

Заряд электрона \( q=1,6 \cdot 10^{-19} \ Кл . \)

Дать ответ в пиконьютонах.

1 пН \( = 10^{-12} \ Н . \)

Ответ: \( F_л= 16 \ \) пН

Дано: \( v=10^8 \ м/с\) \( B=1 \ Тл \) \( q=10^{-6} \ Кл \)
\( \alpha=90^0\)

\(F_л-?\)

\( F_л=Bqv \cdot sin \ \alpha \)

\( F_л=1 \ Тл \cdot 1,6 \cdot 10^{-19} \ Кл \cdot 10^8 \ м/с \cdot sin \ 90^0 =
1,6 \cdot 10^{-11} \ Н \)

\( 1,6 \cdot 10^{-11} \ Н = 16 \ \) пН Ответ: \( F_л= 16 \ \) пН

ПОЗЖЕ

Задача 4. (Сила Лоренца)

С какой скоростью двигался протон в магнитном поле с индукцией \(B=10^{-2} \ Тл\) перпендикулярно линиям поля,
если на него действовала сила Лоренца \(F_л=3,2 \cdot 10^{-17 } \ Н \ ? \)
Заряд протона \( q=1,6 \cdot 10^{-19} \ Кл . \)

Дать ответ в километрах в секунду.

Ответ: \( v= 20 \ км/с \)

Дано: \( B=10^{-2} \ Тл \) \( q=1,6 \cdot 10^{-19} \ Кл \)
\(F_л=3,2 \cdot 10^{-17 } \ Н \) \( \alpha=90^0\)

\(v-?\)

\( F_л=Bqv \cdot sin \ \alpha \)

\(v=\dfrac{F_л}{Bq\cdot sin \ \alpha} \)

\(v=\dfrac{3,2 \cdot 10^{-17 } \ Н }{10^{-2} \ Тл \cdot 1,6 \cdot 10^{-19} \ Кл \cdot sin \ 90^0} = 2 \cdot 10^{4 } \ м/с \)

\( 2 \cdot 10^{4 } \ м/с=20 \ км/с \) Ответ: \( v= 20 \ км/с \)

ПОЗЖЕ

Задача 5. (Сила Лоренца)
Альфа-частица движется в магнитном поле с индукцией \(B=10^{-3} \ Тл\) перпендикулярно линиям поля, при этом на нее действует сила Лоренца \(F_л=6,4 \cdot 10^{-15 } \ Н . \)
Вычислить скорость альфа-частицы, если ее заряд \(q=3,2 \cdot 10^{-19} \ Кл . \)

Дать ответ в километрах в секунду.

Ответ: \( v= 20000 \ км/с \)

Дано: \( B=10^{-3} \ Тл \) \( q=3,2 \cdot 10^{-19} \ Кл \)
\(F_л=6,4 \cdot 10^{-15 } \ Н \) \( \alpha=90^0\)

\(v-?\)

\( F_л=Bqv \cdot sin \ \alpha \)

\(v=\dfrac{F_л}{Bq\cdot sin \ \alpha} \)

\(v=\dfrac{6,4 \cdot 10^{-15 } \ Н }{10^{-3} \ Тл \cdot 3,2 \cdot 10^{-19} \ Кл \cdot sin \ 90^0} = 2 \cdot 10^{7 } \ м/с \)

\( 2 \cdot 10^{7 } \ м/с=20000 \ км/с \) Ответ: \( v= 20000 \ км/с \)

ПОЗЖЕ

Задача 8. (Сила Лоренца)

Протон влетает в магнитное поле со скоростью \(v= 10^{5} \ м/с \) перпендикулярно линиям индукции,
после чего он движется по окружности.Найти радиус этой окружности, если индукция поля
\(B=0,01 \ Тл . \)
Заряд протона \(q=1,6 \cdot 10^{-19} \ Кл \)
Масса протона \(m=1,6 \cdot 10^{-27} \ кг \)

Ответ: \( R=0,1 \ м \)

Запишем формулу второго закона Ньютона для этой задачи:

\( F_{л}=ma_{цс} \)

\( F_{л} \) -сила Лоренца

\( m \) — масса протона

\( a_{цс} \) -центростремительное ускорение протона

Дано: \( v= 10^{5} \ м/с \) \( B=0,01 \ Тл \) \( q=1,6 \cdot 10^{-19} \ Кл \)
\( \alpha=90^0\) \(m=1,6 \cdot 10^{-27} \ кг \)

\(R-?\)

\( Bqv \cdot sin \ \alpha = m \dfrac{v^2}{R} \)

\( R Bqv \cdot sin \ \alpha = m v^2 \)

\( R= \dfrac{mv^2}{ Bqv \cdot sin \ \alpha} \)

\( R= \dfrac{mv}{ Bq \cdot sin \ \alpha} \)

\( R= \dfrac{1,6 \cdot 10^{-27} \ кг \cdot 10^{5} \ м/с }{ 0,01 \ Тл \cdot 1,6 \cdot 10^{-19} \ Кл \cdot sin \ 90^0} =0,1 \ м \) Ответ: \( R=0,1 \ м \)

ПОЗЖЕ

Что с его помощью можно определить

Магнитное поле тока можно усилить, если провод, по которому течет ток, свернуть в форме винтовой спирали. Полученную в результате этого катушку называют соленоидом. Магнитное поле внутри соленоида направлено в сторону, определяемую правилом обхвата правой рукой для катушки с током: если обхватить стержень соленоида ладонью правой руки, направив четыре пальца по току в витках, то оставленный большой палец покажет направление магнитных линий внутри соленоида.

Если длина соленоида много больше его диаметра, то поле внутри него (за исключением пространства вблизи его концов) можно считать практически однородным.

Магнитные поля соленоида и постоянного полосового магнита очень похожи. Как и у магнита, у соленоида есть два полюса — северный (N) и южный (S). Силовые линии магнитного поля выходят из северного полюса и входят в южный. Северный полюс у соленоида всегда находится с той стороны, на которую указывает большой палец в сформированном для соленоида правиле обхвата правой рукой.

Выражение для силы, с которой магнитное поле действует на движущихся заряд, впервые получил физик Хендрик Антон Лоренц. Потому эта сила названа в честь него: 

Fл = qυB sinα

Направление силы Лоренца определяется правилом левой руки для положительно заряженной частицы. Для отрицательно заряженной (например, для электрона), направление силы будет противоположным. 

Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работы. Согласно теореме о кинетической энергии это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости. Под действием силы Лоренца меняется лишь направление движения частицы.

Особенности использования в физике 

Общепринято считать, что направление тока указывает в сторону от плюса к минусу. На самом деле, в проводнике упорядоченное перемещение электронов направлено от негативного полюса к позитивному. Поэтому, если бы перед вами стояла задача вычисления силы Лоренца для отдельного электрона в проводнике, следовало бы учитывать данное обстоятельство.

По умолчанию мы рассматриваем винт (буравчик, штопор) с правой резьбой. Однако не следует забывать о существовании винтов с левой резьбой.

Применение силы Лоренца в технике

Кинескоп

Кинескоп, стоявший до недавнего времени, когда на смену ему пришел LCD-экран (плоский), в каждом телевизоре, не смог бы работать, не будь силы Лоренца. Для формирования на экране телевизионного растра из узкого потока электронов служат отклоняющие катушки, в которых создается линейно изменяющееся магнитное поле. Строчные катушки перемещают электронный луч слева направо и возвращают обратно, кадровые отвечают за вертикальное перемещение, двигая бегающий по горизонтали луч сверху вниз. Такой же принцип используется в осциллографах – приборах, служащих для изучения переменного электрического напряжения.

Watch this video on YouTube

Масс-спектрограф

Масс-спектрограф – прибор, использующий зависимость радиуса вращения заряженной частицы от ее удельного заряда. Принцип его работы следующий:

Источник заряженных частиц, которые набирают скорость с помощью созданного искусственно электрического поля, с целью исключения влияния молекул воздуха помещается в вакуумную камеру. Частицы вылетают из источника и, пройдя по дуге окружности, ударяются в фотопластинку, оставляя на ней следы. В зависимости от удельного заряда меняется радиус траектории и, значит, точка удара. Этот радиус легко измерить, а зная его, можно вычислить массу частицы. С помощью масс-спектрографа, например, изучался состав лунного грунта.

Циклотрон

Независимость периода, а значит, и частоты вращения заряженной частицы от её скорости в присутствии магнитного поля используется в приборе, называемом циклотроном и предназначенном для разгона частиц до высоких скоростей. Циклотрон – это два полых металлических полуцилиндров – дуанта (по форме каждый из них напоминает латинскую букву D), помещенных прямыми сторонами навстречу друг другу на небольшом расстоянии.

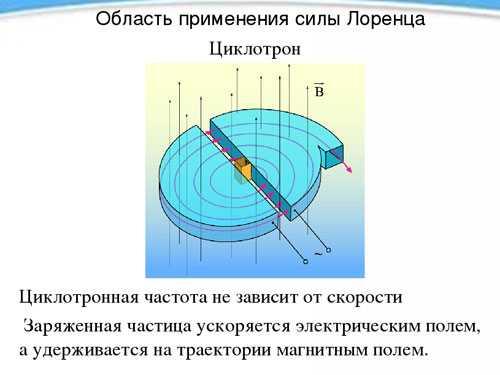
Дуанты помещаются в постоянное однородное магнитное поле, а между ними создается переменное электрическое поле, частота которого равна частоте вращения частицы, определяемой напряженностью магнитного поля и удельным зарядом. Попадая дважды за период вращения (при переходе из одного дуанта в другой) под воздействие электрического поля, частица каждый раз ускоряется, увеличивая при этом радиус траектории, и в определенный момент, набрав нужную скорость, вылетает из прибора через отверстие. Таким способом можно разогнать протон до энергии в 20 МэВ (мегаэлектронвольт).

Магнетрон

Устройство, называемое магнетроном, который установлен в каждой микроволновой печи, – еще один представитель приборов, использующих силу Лоренца. Магнетрон служит для создания мощного СВЧ-поля, которое разогревает внутренний объем печи, куда помещается пища. Магниты, входящие в его состав, корректируют траекторию движения электронов внутри прибора.

Магнитное поле Земли

А в природе сила Лоренца играет крайне важную для человечества роль. Её наличие позволяет магнитному полю Земли защитить людей от смертоносного ионизирующего излучения космоса. Поле не дает возможности заряженным частицам бомбардировать поверхность планеты, заставляя их менять направление движения.

Закон Кулона, определение и формула — электрические точечные заряды и их взаимодействие

Определение направления вектора магнитной индукции с помощью правила буравчика и правила правой руки

Что такое ЭДС индукции и когда возникает?

История открытия электричества

Как перевести амперы в ватты и обратно?

Как подключить однофазный электродвигатель — схема с конденсатором

• Преднамеренное электрическое соединение какой-либо точки сети, электроустановки или оборудования с заземляющим устройством
• Сторонняя проводящая часть, находящаяся в электрическом контакте с землей непосредственно или через промежуточную проводящую среду, используемая для целей заземления
• Заземление точек токоведущих частей электроустановки, выполняемое для обеспечения работы электроустановки

Результаты Poll Options are limited because JavaScript is disabled in your browser.Популярные статьи Как перевести амперы в ватты и обратно? Сколько в ампере ватт, как перевести амперы в ватты и…114.06.2018 Чем отличаются аналоговый сигнал от цифрового — примеры использования Виды сигналов передачи информации, отличие дискретного от цифрового, сравнение цифрового…111.02.2019 Как выполнить перевод люменов в люксы Что такое люмен и люкс, как перевести люксы в люмены,…008.12.2018

Немного истории

Первые попытки описать электромагнитную силу были сделаны еще в XVIII веке. Ученые Генри Кавендиш и Тобиас Майер высказали предположение, что сила на магнитных полюсах и электрически заряженных объектах подчиняется закону обратных квадратов. Однако экспериментальное доказательство этого факта не было полным и убедительным. Только в 1784 году Шарль Августин де Кулон при помощи своего торсионного баланса смог окончательно доказать это предположение.

В 1820 году физиком Эрстедом был открыт факт, что на магнитную стрелку компаса действует ток вольта, а Андре-Мари Ампер в этом же году смог разработать формулу угловой зависимости между двумя токовыми элементами. По сути, эти открытия стали фундаментом современной концепции электрических и магнитных полей. Сама же концепция получила свое дальнейшее развитие в теориях Майкла Фарадея, особенно в его представлении о силовых линиях. Лорд Кельвин и Джеймс Максвелл дополнили теории Фарадея подробным математическим описанием. В частности Максвеллом было создано так званное, «уравнение поля Максвелла» – представляющее собой систему дифференциальных и интегральных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.

Джей Джей Томпсон был первым физиком, кто попытался вывести из уравнения поля Максвелла электромагнитную силу, которые действует на движущийся заряженный объект. В 1881 году он опубликовал свою формулу F = q/2 v x B. Но из-за некоторых просчетов и неполного описания тока смещения она оказалась не совсем правильной.

И вот, наконец, в 1895 году голландский ученый Хендрик Лоренц вывел правильную формулу, которая используется и поныне, а также носит его имя, как и та сила, что действует на летящую частицу в магнитном поле, отныне называется «силой Лоренца».

Хендрик Лоренц.

Действие магнитного поля на ток. Правило левой руки.

Поместим между полюсами магнита проводник, по кото­рому протекает постоянный электрический ток. Мы тотчас же заметим, что проводник будет выталкиваться полем магнита из междуполюсного пространства.

Объяснить это можно следующим образом. Вокруг провод­ника с током (Рисунок 1.) образуется собственное магнитное поле, силовые линии которого по одну сторону проводника направ­лены так же, как и силовые линии магнита, а по другую сто­рону проводника — в противопо­ложную сторону. Вследствие это­го с одной стороны проводника (на рисунке 1 сверху) маг­нитное поле оказывается сгущен­ным, а с другой его стороны (на рисунке 1 снизу) — разрежен­ным. Поэтому проводник испыты­вает силу, давящую на него вниз. И если проводник не закреплен, то он будет перемещаться.

Рисунок 1. Действие магнитного поля на ток.

Правило левой руки

Для быстрого определения направления движения провод­ника с током в, магнитном поле существует так называемое правило левой руки (рисунок 2.).

Рисунок 2. Правило левой руки.

Правило левой руки состоит в следую­щем: если поместить левую руку между полюсами маг­нита так, чтобы магнитные силовые линии входили в ладонь, а четыре пальца ру­ки совпадали с направлением тока в проводнике, то боль­шой палец покажет направ­ление движения проводника.

Итак, на проводник, по которому протекает электри­ческий ток, действует сила, стремящаяся перемещать его перпендикулярно магнитным силовым линиям. Опытным путем можно определить величину этой силы. Оказы­вается, что сила, с которой магнитное поле действует на проводник с током, прямо пропорциональна силе тока в проводнике и длине той части проводника, которая нахо­дится в магнитном поле (рисунок 3 слева).

Это правило справедливо, если проводник расположен под прямым углом к магнитным силовым линиям.

Рисунок 3. Сила взаимодействия магнитного поля и тока.

Если же проводник расположен не под прямым углом к магнитным силовым линиям, а, например, так, как изобра­жено на рисунке 3 справо, то сила, действующая на проводник, будет пропорциональна силе тока в проводнике и длине проекции части проводника, находящейся в магнитном поле, на плос­кость, перпендикулярную магнитным силовым ли­ниям. Отсюда следует, что если проводник паралле­лен магнитным силовым линиям, то сила, дейст­вующая на него, равна нулю. Если же проводник перпендикулярен направ­лению магнитных силовых линий, то сила, действую­щая на него, достигает наибольшей величины.

Сила, действующая на проводник с током, зави­сит еще и от магнитной индукции. Чем гуще рас­положены магнитные си­ловые линии, тем больше сила, действующая на проводник с током.

Подводя итог всему изложенному выше, мы можем действие магнитного поля на проводник с током выразить следующим правилом:

Сила, действующая на проводник с током, прямо пропорциональна магнитной индукции, силе тока в проводнике и длине проекции части проводника, находящейся в магнитном поле, на плоскость, перпендикулярную маг­нитному потоку.

Необходимо отметить, что действие магнитного поля на ток не зависит ни от вещества проводника, ни от его сечения. Дей­ствие магнитного поля на ток можно наблюдать даже при от­сутствии проводника, пропуская, например, между полюсами магнита поток быстро несущихся электронов.

Действие магнитного поля на ток широко используется в науке и технике. На использовании этого действия основано устройство электродвигателей, превращающих электрическую энергию в механическую, устройство магнитоэлектрических приборов для измерения напряжения и силы тока, электроди­намических громкоговорителей, превращающих электрические колебания в звук, специальных радиоламп — магнетронов, катодно-лучевых трубок и т. д. Действием магнитного поля на ток пользуются для измерения массы и заряда электрона и даже для изучения строения вещества.

Похожие материалы:

• Магнитное поле тока. Магнитные силовые линии
• Напряженность магнитного поля
• Магнитная индукция
• Электромагнитная индукция
• Правило правой руки
• Взаимоиндукция
• Самоиндукция
• ЭДС самоиндукции: основные послулаты
• Постоянные магниты

Комментарии

Громова Ева 27.02.2018 18:58 Спасибо большое за статью!

Цитировать

асаев антон 04.09.2014 04:56 спасибо создателю сайта

Цитировать

Обновить список комментариев

Понятие напряженности электрического поля

Электромагнитное поле на самом деле состоит из двух половин – электрической и магнитной. Они точно близнецы, у которых все одинаково, но вот характер разный. А если приглядеться, то во внешности можно заметить небольшие различия.

То же самое касается и силовых полей. Электрическое поле тоже обладает напряженностью – векторной величиной, которая является силовой характеристикой. Она воздействует на частицы, которые в неподвижности находятся в нем

Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей

Напряженность электрического поля

Напряженность электрического поля воздействует только на неподвижный заряд и определяется по формуле:

Единицей измерения является Н/Кл или В/м.

Как направлена сила Лоренца

Чтобы определить направление силы Лоренца, как и с силой Ампера, работает правило левой руки. Это значит, чтобы понять, куда направлено значение Fл нужно раскрыть ладонь левой руки так, чтобы в руку входили линии магнитной индукции, а вытянутые четыре пальца указывали направление вектора скорости. Тогда большой палец, отогнутый под прямым углом к ладони, указывает направление силы Лоренца. На картинке ниже вы видите, как определить направление.

Внимание! Направление Лоренцового действия перпендикулярно движению частицы и линиям магнитной индукции. При этом, если быть точнее, для положительно и отрицательно заряженных частиц имеет значение направление четырёх развернутых пальцев

Выше описанное правило левой руки сформулировано для положительной частицы. Если она заряжена отрицательно, то линии магнитной индукции должны быть направлены не в раскрытую ладонь, а в её тыльную сторону, а направление вектора Fл будет противоположным

При этом, если быть точнее, для положительно и отрицательно заряженных частиц имеет значение направление четырёх развернутых пальцев. Выше описанное правило левой руки сформулировано для положительной частицы. Если она заряжена отрицательно, то линии магнитной индукции должны быть направлены не в раскрытую ладонь, а в её тыльную сторону, а направление вектора Fл будет противоположным.

Теперь мы расскажем простыми словами, что даёт нам это явление и какое реальное воздействие она оказывает на заряды. Допустим, что электрон движется в плоскости, перпендикулярной направлению линий магнитной индукции. Мы уже упомянули, что Fл не воздействует на скорость, а лишь меняет направление движения частиц. Тогда сила Лоренца будет оказывать центростремительное воздействие. Это отражено на рисунке ниже.