Природа магнетизма: магнитный поток, определение, свойства, общая характеристика

Отрывок, характеризующий Магнитный поток

В ноябре месяце 1805 года князь Василий должен был ехать на ревизию в четыре губернии. Он устроил для себя это назначение с тем, чтобы побывать заодно в своих расстроенных имениях, и захватив с собой (в месте расположения его полка) сына Анатоля, с ним вместе заехать к князю Николаю Андреевичу Болконскому с тем, чтоб женить сына на дочери этого богатого старика. Но прежде отъезда и этих новых дел, князю Василью нужно было решить дела с Пьером, который, правда, последнее время проводил целые дни дома, т. е. у князя Василья, у которого он жил, был смешон, взволнован и глуп (как должен быть влюбленный) в присутствии Элен, но всё еще не делал предложения.

Среди многих определений и понятий, связанных с магнитным полем, следует особо выделить магнитный поток, обладающий определенной направленностью. Это свойство широко используется в электронике и электротехнике, в конструкциях приборов и устройств, а также при расчете различных схем.

Что такое магнитный поток?

Для того чтобы дать точную количественную формулировку закона электромагнитной индукции Фарадея, нужно ввести новую величину — поток вектора магнитной индукции.

Вектор магнитной индукции характеризует магнитное поле в каждой точке пространства. Можно ввести еще одну величину, зависящую от значений вектора не в одной точке, а во всех точках поверхности, ограниченной плоским замкнутым контуром.

Для этого рассмотрим плоский замкнутый проводник (контур), ограничивающий поверхность площадью S и помещенный в однородное магнитное поле (рис. 2.4). Нормаль (вектор, модуль которого равен единице) к плоскости проводника составляет угол с направлением вектора магнитной индукции . Магнитным потоком Ф (потоком Вектора магнитной индукции) через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции на площадь S и косинус угла между векторами  и :Произведение представляет собой проекцию вектора магнитной индукции на нормаль к плоскости контура. ПоэтомуМагнитный поток тем больше, чем больше В_n и S. Величина Ф названа «магнитным потоком» по аналогии с потоком воды, который тем больше, чем больше скорость течения воды и площадь сечения трубы.

Магнитный поток графически можно истолковать как величину, пропорциональную числу линий магнитной индукции, пронизывающих поверхность площадью S.

Единицей магнитного потока является вебер. Магнитный поток в 1 вебер (1 Вб) создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции.

Магнитный поток зависит от ориентации поверхности, которую пронизывает магнитное поле.

Проводящая рамка в магнитном поле

Явление электромагнитной индукции состоит в том, что при изменении поля, пронизывающего проводящую рамку или катушку, в ней возникает электродвижущая сила (ЭДС):

Рис. 1. Электромагнитная индукция, эксперимент Фарадея.

Энергия магнитного поля, используемая в этом эксперименте, характеризуется магнитной индукцией. Однако при попытке описать наблюдаемое явление оказалось, что одного этого значения недостаточно.

Если мы запишем в таблицу значения ЭДС, индуцированной магнитным полем, имеющим одинаковую плотность магнитных линий в разных условиях, то окажется, что ЭДС, возникающая в квадратной рамке, имеет гораздо большее значение, чем ЭДС в рама длинная и узкая (по периметру).

И самая большая ЭДС возникает в круглом цикле.

Причиной тому была разная «зона покрытия» шасси. Длинная узкая область кадра невелика, она «закрывает» небольшое «поле» и ЭДС внутри нее также мала. Квадратная рамка имеет наибольшую площадь с тем же периметром, а круглое кольцо – наибольшую, следовательно, рамка «покрывает» большее «количество поля», и ЭДС в этом кадре также больше.

Не менее важной оказалась ориентация рамки относительно направления магнитного поля. Наибольшая ЭДС возникает, если проводящая рамка перпендикулярна линиям магнитной индукции

Если плоскость кадра параллельна этим линиям, то, независимо от его площади и силы магнитного поля, ЭДС не будет отображаться в кадре.

Теорема Гаусса для магнитной индукции

Что является источником магнитного поля.

Великий немецкий учёный Карл Гаусс, который отличился в математике, физике и астрономии, вывел закон (теорему) в области магнетизма. Он доказал, что, в отличие от электрического поля, создаваемого электрическими зарядами, МП не создаётся зарядами магнитными. Их попросту не существует в классической электродинамике.

Информация.Теорема, которую вывел Гаусс, принадлежит к главным законам электродинамики и является частью системы уравнений Максвелла. Она описывает соотношение между потоком напряжённости электрополя, пронизывающего замкнутую произвольную поверхность, и суммой зарядов, помещающихся в очерченном этой поверхностью объёме. Сумма выражена в алгебраической форме.

В отношении магнитной индукции поток В→, проходящий через замкнутую поверхность S, имеет нулевое значение. 

Конвертер величин

Калькуляторы

В этой части Конвертера физических единиц TranslatorsCafe.com представлена группа калькуляторов, выполняющих расчеты в различных областях электротехники, радиотехники и электроники.

Магнитостатика, магнетизм и электродинамика

Магнитостатика — раздел классической электродинамики, изучающий взаимодействие постоянных токов посредством создаваемого ими постоянного магнитного поля и способы расчета магнитного поля в этом случае.

Электродинамика

— раздел физики, изучающий силы, возникающие при взаимодействии электрически заряженных частиц и тел. Эти силы объясняются в электродинамике с помощью электромагнитных полей. Силы электромагнитного взаимодействия лежат в основе большинства явлений, с которыми мы встречаемся в повседневной жизни. Часть привычных явлений обусловлена действием гравитационных сил.

Электромагнитное поле

— физическое поле, появляющееся при взаимодействии движущихся заряженных телами или частиц. Электромагнитное поле можно рассматривать как сочетание электрического и магнитного полей.

Электрическое поле

— физическое поле, окружающее электрически заряженные частицы, проводники с проходящими в них электрическими токами и изменяющиеся во времени и пространстве магнитные поля.

Магнитное поле

— физическое силовое поле, окружающее заряженные частицы, проводники с электрическим током, магнитные материалы и переменные электрические поля, а также действующее на проводники с электрическим током, движущиеся электрические заряды и тела, обладающие магнитным моментом. Магнитное поле в любой точке определяется направлением и силой и таким образом является векторным полем. Магнитное поле характеризуется двумя основными величинам — вектором магнитной индукцииВ и вектором напряженности магнитного поляH .

Конвертер магнитного потока

Магнитный поток

определяется как интеграл вектора магнитной индукции через конечную поверхность. Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади. Для измерения магнитного потока используют флюксметр, который измеряет напряжение на измерительной катушке.

В СИ единицей магнитного потока является вебер

(Вб, размерность — В·с = кг·м²·с⁻²·А⁻¹). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м². В системе СГС — магнитный поток измеряется вмаксвеллах (Мкс).

Использование конвертера «Конвертер магнитного потока»

На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.

Изучайте технический английский язык и технический русский язык с нашими видео! — Learn technical English and technical Russian with our videos!

Пользуйтесь конвертером для преобразования нескольких сотен единиц в 76 категориях или несколько тысяч пар единиц, включая метрические, британские и американские единицы. Вы сможете перевести единицы измерения длины, площади, объема, ускорения, силы, массы, потока, плотности, удельного объема, мощности, давления, напряжения, температуры, времени, момента, скорости, вязкости, электромагнитные и другие. Примечание.

В связи с ограниченной точностью преобразования возможны ошибки округления. В этом конвертере целые числа считаются точными до 15 знаков, а максимальное количество цифр после десятичной запятой или точки равно 10.

Для представления очень больших и очень малых чисел в этом калькуляторе используется компьютерная экспоненциальная запись

, являющаяся альтернативной формой нормализованной экспоненциальной (научной) записи, в которой числа записываются в форме a · 10x. Например: 1 103 000 = 1,103 · 106 = 1,103E+6. Здесь E (сокращение отexponent ) — означает «· 10^», то есть«…умножить на десять в степени…» . Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах.

Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.

Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!

Канал Конвертера единиц TranslatorsCafe.com на YouTube

Магнитный поток

Магнитный поток – это скалярная величина, которая характеризует влияние магнитной индукции на данный металлический контур.

Магнитная индукция определяется количеством силовых линий, пересекающих 1 см2 металлического сечения.

Магнитометры, используемые для его измерения, называются теслометрами.

После прекращения движения электронов в катушке сердечник, если он сделан из мягкого железа, теряет свои магнитные свойства. Если он изготовлен из стали, он может некоторое время сохранять свои магнитные свойства.

Взаимодействие магнитов

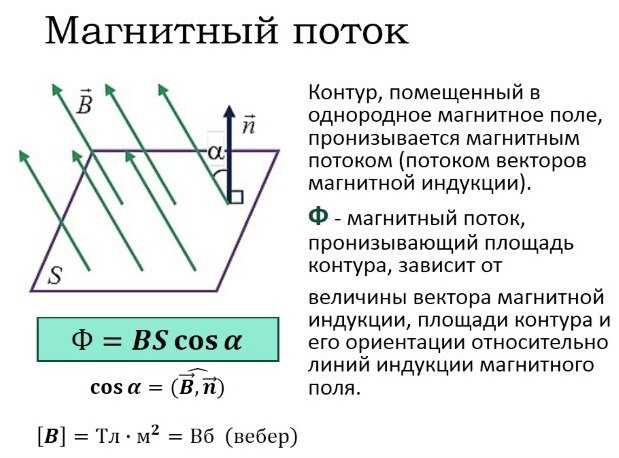
Постоянный магнит (или магнитная стрелка) ориентирован по магнитному меридиану Земли. Конец, указывающий на север, называется северным полюсом (N), а противоположный конец – южным полюсом (S). Поднося два магнита ближе, мы замечаем, что одноименные полюса отталкиваются друг от друга, а противоположные – притягиваются (рис. 1).

Если мы разделим полюса, разрезав постоянный магнит на две части, мы обнаружим, что каждая из них также будет иметь по два полюса, то есть это будет постоянный магнит (рис. 2). Оба полюса – север и юг – неотделимы друг от друга, равны.

Магнитное поле, создаваемое Землей или постоянными магнитами, представлено, как электрическое поле, магнитными силовыми линиями. Изображение силовых линий магнитного поля магнита можно получить, положив поверх него лист бумаги, на который ровным слоем насыпают железные опилки. Попадая в магнитное поле, опилки намагничиваются: у каждого из них есть северный и южный полюс. Противоположные полюса имеют тенденцию сближаться, но этому препятствует трение опилок о бумагу. Если вы коснетесь бумаги пальцем, трение уменьшится, и опилки будут притягиваться друг к другу, образуя цепочки, которые представляют собой силовые линии магнитного поля.

На рис. 3 показано положение в поле прямого магнита из опилок и маленькие магнитные стрелки, указывающие направление силовых линий магнитного поля. Это направление принимается за направление северного полюса магнитной стрелки.

Магнитное поле. Вектор магнитной индукции. Правило буравчика. Закон Ампера и сила Ампера. Сила Лоренца. Правило левой руки. Электромагнитная индукция, магнитный поток, правило Ленца, закон электромагнитной индукции, самоиндукция, энергия магнитного поля

Магнитное поле. Вектор магнитной индукции. Правило буравчика:

Магнитное поле: это особая форма, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами

• Вектор магнитной индукции B : это силовая характеристика магнитного поля. Направление В это направление от южного полюса к северному полюсу магнитной стрелки, свободно устанавливающейся в магнитном поле (совпадает с направлением положительной нормали к замкнутому контуру с током).
• Правило Буравчика: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора В.
• Модуль вектора магнитной индукции В — это отношение максимальной силы F_m, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока I на длину этого участка Δl :

Сила Ампера, Закон Ампера, правило левой руки:

• Сила Ампера: это сила, действующая на проводник с током, помещенный в магнитное поле
• Закон Ампера: сила Ампера равна произведению модуля вектора магнитной индукции на силу тока, длину участка проводника Δl и на синус угла α между магнитной индукцией и участком проводника:
  • при этом, очевидно, что если ток (проводник) перпендикулярен вектору магнитной индукции, то
  • sin α = 1, и формула принимает вид:

Правило левой руки: если левую руку расположить так, чтобы перпендикулярная к проводнику составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению движения тока, то отогретый на 90 о большой палец покажет направление силы, действующей на отрезок проводника

Сила Лоренца, правило левой руки:

• Сила Лоренца: это сила, действующая на движущуюся заряженную частицу со стороны магнитного поля:
  • при этом, очевидно, что если скорость частицы перпендикулярна вектору магнитной индукции,
  • то sin α = 1, и формула принимает вид:

Правило левой руки: если левую руку расположить так, чтобы составляющая вектора В перпендикулярная скорости заряда входила в ладонь, а четыре вытянутых пальца были направлены по движении положительного заряда (= против движения отрицательного заряда), то отогрутый на 90 о большой палец покажет направление действующей заряд силы Лоренца

Явление электромагнитной индукции, магнитный поток, поток магнитной индукции:

Электромагнитная индукция: это явление возникновения электрического тока в проводящем контуре, который либо покоится в переменном магнитном поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих контур, меняется

• Магнитный поток (=поток магнитной индукции) : через поверхность площадью S это величина равная произведению модуля вектора магнитной индукции В на площадь и косинус угла между вектром В и нормалью к плоскости S:
  • при этом, очевидно, что если магнитная индукция перпендикулярна плоскости,
  • то cos α = 1, и формула принимает вид:

Правило Ленца:

Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного поля, которым он вызван.

Закон электромагнитной индукции:

ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока через поверхность, ограниченную контуром, взатой со знаком «-»

Самоиндукция:

Самоиндукция это частный случай электромагнитной индукции, при котором изменяющееся магнитное поле индуцирует ЭДС в том самом проводнике, по которому течет ток, создающий это поле:

Энергия магнитного поля тока:

Энергия магнитного поля тока: Энергия магнитного поля тока равна работе, которую должен совершить источник, чтобы создать данный ток

Консультации и техническая поддержка сайта: Zavarka Team

Появление понятия магнитной индукции

На заре эпохи развития электричества люди стали исследовать сопутствующие явления. Так, Ханс Эрстед в 1819 году обнаружил: проводник с током создает вокруг круговое магнитное поле, Андре-Мари Ампер показал, что если направление движения зарядов совпадает, соседствующие проводники притягивают друг друга. Конец спорам положило создание закона Био-Савара (отечественные источники добавляют Лапласа), описывающего величину, направление магнитной индукции в точке пространства. Источники допускают оговорку касательно того, что исследования велись постоянного тока.

Взаимосвязь индукции и напряженности магнитного поля

Интегрирование (см. рисунок) идет по контуру с током. В формуле r подразумевает элементарную среднюю точку текущего отрезка, r0 – место пространства, для которого вычисляется магнитная индукция

Обратите внимание, в знаменателе дроби за интегралом перемножаются два вектора. Результатом выходит величина, направление которой определим по правилу буравчика (левой или правой руки). Интегрирование ведется по элементу контура dr, r – средняя точка малого отреза полной длины

Идентичные разности в числителе и знаменателе сократим, остается вверху единичный вектор, задающий направление результата

Интегрирование ведется по элементу контура dr, r – средняя точка малого отреза полной длины. Идентичные разности в числителе и знаменателе сократим, остается вверху единичный вектор, задающий направление результата.

Формула показывает, как найти поле для контуров любой формы, проводя интегрирование по точкам. Современные численные методы лежат в основе действия компьютерных приложений (наподобие Maxwell 3D) по решению соответствующей задачи. Уравнение согласуется с законами Гаусса (магнитной индукции) и Ампера (циркуляции магнитного поля). Георг Ом использовал знания о компасе, выводя известную зависимость. Форму линий поля получим при помощи магнитных стрелок и силы оставления направления неизменным (см. заметку про закон Ома для участка цепи). Это будет картина магнитной индукции в пространстве, экспериментально подтвердившая закон Био-Савара-Лапласа.

Позволило сделанное Амперу в 1825 году показать: электрический ток в некоторых случаях является аналогом постоянного магнита. Появилась новая модель, которая лучше согласовывалась с действительностью, нежели схема диполей Пуассона. Подобная абстракция объясняла отсутствие в природе изолированных магнитных полюсов. По современным представлениям, кусок стали намагничивается, оттого что диполи элементарных частиц и молекул приобретают упорядоченность. На этом основаны контуры размагничивания сердечников трансформаторов, которые перед выключением питания вызывают затухающие колебания тока. В результате эффект упорядоченности размывается, выраженные свойства пропадают.

Спин электрона

Наличие магнитного момента объясняется существованием спинов (понятие введено в 20-х годах XX века) – угловой момент частиц микромира. Реальные, не абстрактные вещи, существование подтверждено экспериментально (Штерн-Герлах). Спин является векторной величиной, одинаковой для всех частиц одного типа (например, электронов), описывается специальным квантовым числом. В СИ единицей измерений служит Дж с, как и для другого углового момента (постоянной Планка). Иногда применяется упрощенная безразмерная запись. Постоянная Планка опускается. Указывается просто спиновое квантовое число (s, ms).

Благодаря наличию спина, элементарная частица обзаводится магнитным моментом, вычисляемым по формуле: в числителе произведение спинового углового момента на заряд частицы и g-фактор (постоянные, приводимые в различных справочниках для тех или иных элементарных частиц); в знаменателе – удвоенная масса элементарной частицы. Как видите, поддается учету, максимальную намагниченность материала в заданных условиях можно заранее рассчитать. Настоящим триумфом квантовой электродинамики явилось предсказание g-факторов для некоторых элементарных частиц.

Открытие Майклом Фарадеем в 1831 году генерации переменным магнитным полем кругового электрического показало: два явления тесно связаны, что явилось предпосылкой созданию (четырех) уравнений Максвелла, частным случаем которых являются большинство формул в этой области, считая упомянутые выше. Исследования шли своим чередом, но несколько разными путями. Интеграцию произвел лорд Кельвин, известный как Вильям Томпсон, который показал наличие H (напряженность) и B магнитной индукции, первая характеризует модель Пуассона, вторая – Ампера.

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

(Здесь формулы приведем в СИ, в виде для вакуума, где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике

В магнитостатическом пределе наиболее важными являются:

• Закон Био — Савара — Лапласа: играет в магнитостатике ту же роль, что закон Кулона в электростатике:

  B→(r→)=μ4π∫L1I(r→1)dL1→×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int \limits _{L_{1}}{\frac {I\left({\vec {r}}_{1}\right){\vec {dL_{1}}}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}

  B→(r→)=μ4π∫j→(r→1)dV1×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int {\frac {{\vec {j}}\left({\vec {r}}_{1}\right)dV_{1}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}

• Теорема Ампера о циркуляции магнитного поля:

  ∮∂S⁡B→⋅dl→=μIS≡μ∫Sj→⋅dS→,{\displaystyle \oint \limits _{\partial S}{\vec {B}}\cdot {\vec {dl}}=\mu _{0}I_{S}\equiv \mu _{0}\int \limits _{S}{\vec {j}}\cdot {\vec {dS}},}

  rotB→≡∇→×B→=μj→.{\displaystyle \mathrm {rot} \,{\vec {B}}\equiv {\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {j}}.}

В общем случае

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции B→{\displaystyle {\vec {B}}}:

Три из четырех уравнений Максвелла (основных уравнений электродинамики)

divE→=ρε,   rotE→=−∂B→∂t{\displaystyle \mathrm {div} \,{\vec {E}}={\frac {\rho }{\varepsilon _{0}}},\ \ \ \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}}

divB→=,    rotB→=μj→+1c2∂E→∂t{\displaystyle \mathrm {div} \,{\vec {B}}=0,\ \ \ \ \,\mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}}

а именно:

Закон отсутствия монополя:

divB→=,{\displaystyle \mathrm {div} \,{\vec {B}}=0,}

Закон электромагнитной индукции Фарадея:

rotE→=−∂B→∂t,{\displaystyle \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},}

Закон Ампера — Максвелла:

rotB→=μj→+1c2∂E→∂t.{\displaystyle \mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}.}

Формула силы Лоренца:

F→=qE→+qv→×B→,{\displaystyle {\vec {F}}=q{\vec {E}}+q\left,}

Следствия из неё, такие как

Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)

dF→=Idl→×B→,{\displaystyle d{\vec {F}}=\left,}

dF→=j→dV×B→,{\displaystyle d{\vec {F}}=\left,}

выражение для момента силы, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):

M→=m→×B→,{\displaystyle {\vec {M}}={\vec {m}}\times {\vec {B}},}

выражение для потенциальной энергии магнитного диполя в магнитном поле:

U=−m→⋅B→,{\displaystyle U=-{\vec {m}}\cdot {\vec {B}},}

• а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т. д..
• Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:

F→=Kqmr→r3.{\displaystyle {\vec {F}}=K{\frac {q_{m}{\vec {r}}}{r^{3}}}.}

(это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

Выражение для плотности энергии магнитного поля

w=B22μ{\displaystyle w={\frac {B^{2}}{2\mu _{0}}}}

Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Энергия магнитного поля и поток магнитной индукции

Если по проводнику пропустить электрический ток, то вокруг него образуется магнитное поле, обладающее энергией. Ее происхождение связано с электроэнергией источника тока, которая частично расходуется для преодоления ЭДС самоиндукции, возникающей в цепи. Это так называемая собственная энергия тока, за счет которой и образуется . То есть, энергии поля и тока будут равны между собой.

Значение собственной энергии тока выражает формула W = (L x I 2)/2. Это определение считается равной той работе, которая совершается источником тока, преодолевающим индуктивность, то есть, ЭДС самоиндукции и создающим ток в электрической цепи. Когда ток прекращает действовать энергия магнитного поля не пропадает бесследно, а выделяется, например, в виде дуги или искры.

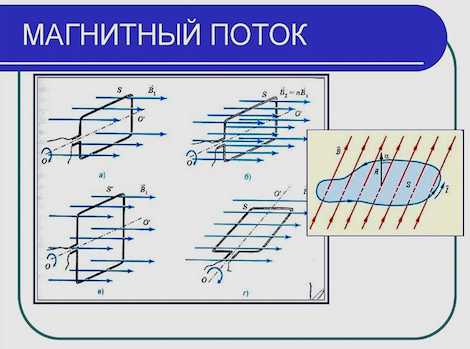
Магнитный поток, возникающий в поле, известен еще и как поток магнитной индукции с положительным или отрицательным значением, направление которого условно обозначено вектором. Как правило, проходит этот поток через контур, по которому протекает электрический ток. При положительном направлении нормали относительно контура, направление движения тока есть величина, определяемая в соответствии с . В этом случае магнитный поток, создаваемый контуром с электрическим током, и проходящий через этот контур, всегда будет иметь значение больше нулевого. На это указывают и практические измерения.

Обычно измеряется магнитный поток в единицах, установленных международной системой СИ. Это уже известный вебер, представляющий собой величину потока, проходящего через плоскость с площадью 1 м2. Данная поверхность размещается перпендикулярно по отношению к силовым линиям магнитного поля с однородной структурой.

Это понятие хорошо описывает теорема Гаусса. В ней отражено отсутствие магнитных зарядов, поэтому индукционные линии всегда представляются замкнутыми или уходящими в бесконечность без начала и конца. То есть, магнитный поток, проходящий через любые виды замкнутых поверхностей, всегда равен нулю.

На
картинке показано однородное магнитное
поле. Однородное означает одинаковое
во всех точках в данном объеме. В поле
помещена поверхность с площадью S. Линии
поля пересекают поверхность.

Определение
магнитного потока
:

Магнитным
потоком Ф через поверхность S называют
количество линий вектора магнитной
индукции B, проходящих через поверхность
S.

Формула
магнитного потока:

здесь
α — угол между направлением вектора
магнитной индукции B и нормалью к
поверхности S.

Из
формулы магнитного потока видно, что
максимальным магнитный поток будет при
cos α = 1, а это случится, когда вектор B
параллелен нормали к поверхности S.
Минимальным магнитный поток будет при
cos α = 0, это будет, когда вектор B
перпендикулярен нормали к поверхности
S, ведь в этом случае линии вектора B
будут скользить по поверхности S, не
пересекая её.

А
по определению магнитного потока
учитываются только те линии вектора
магнитной индукции, которые пересекают
данную поверхность.

Измеряется
магнитный поток в веберах (вольт-секундах):
1 вб = 1 в * с. Кроме того, для измерения
магнитного потока применяют максвелл:
1 вб = 10 8 мкс.
Соответственно 1 мкс = 10 -8 вб.

Магнитный
поток является скалярной величиной.

ЭНЕРГИЯ
МАГНИТНОГО ПОЛЯ ТОКА

Вокруг
проводника с током существует магнитное
поле, которое обладает энергией.
Откуда
она берется? Источник тока, включенный
в эл.цепь, обладает запасом энергии.
В
момент замыкания эл.цепи источник тока
расходует часть своей энергии на
преодоление действия возникающей ЭДС
самоиндукции. Эта часть энергии,
называемая собственной энергией тока,
и идет на образование магнитного
поля.
Энергия магнитного поля
равна собственной
энергии тока.
Собственная
энергия тока численно равна работе,
которую должен совершить источник тока
для преодоления ЭДС самоиндукции, чтобы
создать ток в цепи.

Энергия
магнитного поля, созданного током, прямо
пропорциональна квадрату силы тока.
Куда
пропадает энергия магнитного поля после
прекращения тока? — выделяется (при
размыкании цепи с достаточно большой
силой тока возможно возникновение искры
или дуги)

Невидимая сила

Магниты имеют свойство притягивать к себе некоторые металлы, особенно железо и сталь, а также никель, сплавы никеля, хрома и кобальта. Материалы, создающие силы притяжения, являются магнитами. Существуют различные их типы. Материалы, которые могут легко намагничиваться, называются ферромагнитными. Они могут быть жесткими или мягкими. Мягкие ферромагнитные материалы, такие как железо, быстро теряют свои свойства. Магниты, изготовленные из этих материалов, называются временными. Жесткие материалы, такие как сталь, держат свои свойства гораздо дольше и используются в качестве постоянных.

Постоянные магниты

Источником магнитного поля (МП) могут служить постоянные магниты. Они изготавливаются из магнетита. В природе он известен как оксид железа. Это минерал чёрной окраски, имеющий молекулярное строение FeO·Fe2O3. Свойства магнитов известны с давних времён. Магниты имеют два полюса – северный и южный.

Постоянные магниты можно классифицировать по следующим критериям:

• материал, из которого изготовлен магнит;
• форма;
• сфера использования.

Магниты с постоянными полюсами изготавливаются из различных материалов:

• ферритов – прессованных изделий из порошков оксида железа и оксидов иных металлов;
• редкоземельных – нодимовых (NdFeB), самариевых (SmCo), литых (сплавы металлов), полимерных (магнитопласты).

Форма магнитов самая различная:

• цилиндрическая (прямоугольная);
• подковообразная;
• кольцеобразная;
• дискообразная.

Направление линий МП в зависимости от формы магнита

Постоянные магниты нашли широкое применение в различных отраслях народного хозяйства:

• МРТ – медицинский прибор для диагностики человеческого организма;
• приводы жёстких дисков в современных компьютерах;
• в радиотехнике, при изготовлении динамиков;
• производство декоративных украшений с применением магнитов на полимерной основе.

В двигателях постоянного тока такие магниты вмонтированы в корпус индуктора.