Интерференция волн

2.1. Сложение гармонических колебаний одного направления

1. Сложение двух колебаний одного направления (сонаправленных колебаний)

можно провести с помощью метода векторных диаграмм (Рисунок 9) вместо сложения двух уравнений.

На Рисунке 2.1 показаны векторы амплитуд А₁(t) и А₂(t) складываемых колебаний в произвольный момент времени t, когда фазы этих колебаний соответственно равны и . Сложение колебаний сводится к определению . Воспользуемся тем фактом, что на векторной диаграмме сумма проекций складываемых векторов равна проекции векторной суммы этих векторов.

Результирующему колебанию соответствует на векторной диаграмме вектор амплитуды и фаза .

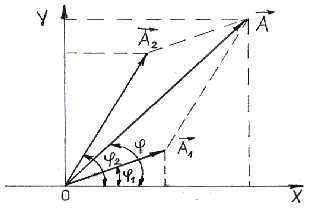
Рисунок 2.1 – Сложение сонаправленных колебаний.

Величина вектора А(t) может быть найдена по теореме косинусов:

.

Фаза результирующего колебания задается формулой:

.

Если частоты складываемых колебаний ω₁ и ω₂ не равны, то и фаза φ(t), и амплитуда А(t) результирующего колебания будут изменяться с течением времени. Складываемые колебания называются некогерентными в этом случае.

2. Два гармонических колебания x₁ и x₂ называются когерентными, если разность их фаз не зависит от времени:

.

Но так как , то для выполнения условия когерентности двух этих колебаний должны быть равны их циклические частоты .

Амплитуда результирующего колебания, полученного при сложении сонаправленных колебаний с равными частотами (когерентных колебаний) равна:

.

Начальную фазу результирующего колебания легко найти, если спроектировать векторы А₁ и А₂ на координатные оси ОХ и ОУ (см. Рисунок 9):

.

Итак, результирующее колебание, полученное при сложении двух гармонических сонаправленных колебаний с равными частотами, также является гармоническим колебанием .

3. Исследуем зависимость амплитуды результирующего колебания от разности начальных фаз складываемых колебаний.

Если , где n – любое целое неотрицательное число

(n = 0, 1, 2…), то , т.е. результирующая амплитуда будет минимальной. Складываемые колебания в момент сложения находились в противофазе. При результирующая амплитуда равна нулю .

Если , то , т.е. результирующая амплитуда будет максимальной. В момент сложения складываемые колебания находились в одной фазе, т.е. были синфазны. Если амплитуды складываемых колебаний одинаковы , то .

4. Сложение сонаправленных колебаний с неравными, но близкими частотами.

Частоты складываемых колебаний не равны , но разность частот много меньше и ω₁, и ω₂. Условие близости складываемых частот записывается соотношениями .

Примером сложения сонаправленных колебаний с близкими частотами является движение горизонтального пружинного маятника, жесткость пружин которого немного различна k₁ и k₂.

Пусть амплитуды складываемых колебаний одинаковы, а начальные фазы равны нулю . Тогда уравнения складываемых колебаний имеют вид: , .

Результирующее колебание описывается уравнением:

.

Получившееся уравнение колебаний зависит от произведения двух гармонических функций: одна – с частотой , другая – с частотой , где ω близка к частотам складываемых колебаний (ω₁ или ω₂). Результирующее колебание можно рассматривать как гармоническое колебание с изменяющейся по гармоническому закону амплитудой. Такой колебательный процесс называется биениями. Строго говоря, результирующее колебание в общем случае не является гармоническим колебанием.

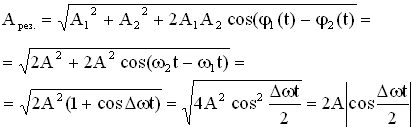Абсолютное значение косинуса взято потому, что амплитуда – величина положительная. Характер зависимости х_рез.при биениях показан на Рисунке 2.2.

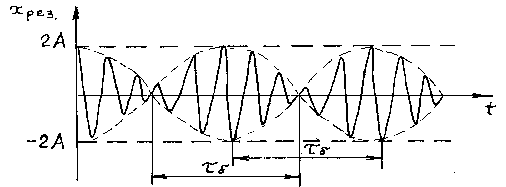
Рисунок 2.2 – Зависимость смещения от времени при биениях.

Амплитуда биений медленно меняется с частотой . Абсолютное значение косинуса повторяется, если его аргумент изменяется на π, значит и значение результирующей амплитуды повторится через промежуток времени τ_б, называемый периодом биений (см. Рисунок 12). Величину периода биений можно определить из следующего соотношения:

.

Величина — период биений.

Величина есть период результирующего колебания (Рисунок 2.4).

См. также

Wikimedia Foundation . 2010 .

Смотреть что такое «Когерентные волны» в других словарях:

когерентные волны — Волны, разность фаз которых не зависит от времени. Тематики виды (методы) и технология неразр.… … Справочник технического переводчика

когерентные волны — koherentinės bangos statusas T sritis fizika atitikmenys: angl. coherent waves vok. kohärente Wellen, f rus. когерентные волны, f pranc. ondes cohérentes, f … Fizikos terminų žodynas

когерентные волны — (связанные волны) волны одинаковой частоты, колебания в которых отличаются постоянной разностью фаз, не изменяющейся со временем … Русский индекс к Англо-русскому словарь по музыкальной терминологии

когерентные световые волны — Световые волны, имеющие постоянную разность фаз световых колебаний в течение данного отрезка времени. Тематики… … Справочник технического переводчика

ВОЛНЫ — (1) (см.), распространяющиеся с конечной скоростью в пространстве и несущие с собой энергию без переноса вещества; (2) В. де Бройля проявляются при движении любой микрочастицей и отражают одновременное сочетание волновых и корпускулярных свойств… … Большая политехническая энциклопедия

электромагнитные волны — электромагнитное поле, распространяющееся в пространстве с конечной скоростью, зависящей от свойств среды. В вакууме скорость распространения электромагнитной волны с≈300 000 км/с (см. Скорость света). В однородных изотропных средах направления… … Энциклопедический словарь

Когерентность — (от латинского cohaerens находящийся в связи) согласованное протекание во времени нескольких колебательных или волновых процессов, проявляющееся при их сложении. Колебания называются когерентными, если разность их фаз остаётся постоянной… … Большая советская энциклопедия

Интерференция (физич.) — Картина интерференции двух круговых когерентных волн, в зависимости от длины волны и расстояния между источниками Интерференция волн наложение волн, при котором происходит их взаимное усиление в одних точках пространства и ослабление – в других.… … Википедия

Интерференция волн — Это статья об интерференции в физике. См. также Интерференция и Интерференция света Картина интерференции большого количества круговых когерентных волн, в зависимости от длины волны и расстояния между источниками Интерференция волн взаимное … Википедия

Интерференция (физика) — Это статья об интерференции в физике. См. также Интерференция (неоднозначность) и Интерференция света Картина интерференции двух круговых когерентных волн, в зависимости от длины волны и расстояния между источниками Интерференция волн нелинейное… … Википедия

Физическое понятие когерентности представляет собой несколько согласованных по времени колебаний или волн, проявление которых наступает во время их сложения. Колебания считаются когерентными, когда их различные фазы имеют временное постоянство. Сумма колебаний имеет ту же частоту, как и каждое отдельное колебание. Таким образом, когерентные источники света работают на основе двух синусоидальных колебаний с одной и той же частотой.

Квазистационарный ток

Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводников, созданного поверхностными зарядами, будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц и, следовательно, гармонические колебания силы тока.

Правда, при изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменения поля распространяются хотя и с очень большой, но не бесконечно большой скоростью.

Однако, если время распространения изменения поля в цепи много меньше периода Т колебаний напряжения, можно считать, что электрическое поле во всей цепи сразу же меняется при изменении напряжения на концах цепи. При этом сила тока в данный момент времени имеет практически одно и то же значение во всех сечениях неразветвленной цепи.

Такой медленно меняющийся переменный ток называется квазистационарным. Если длина цепи l, то время распространения изменений электрического поля от одного конца цепи до другого определяется величиной где с = 3 • 108 м/с — скорость распространения электромагнитных взаимодействий (скорость света). Для переменного тока периодом Т условие квазистационарности запишется так:

Период электрических колебаний квазистационарного тока должен быть много больше времени распространения в цепи электромагнитных возмущений. При частоте ν = 50 Гц длина цепи должна быть много меньше расстояния: l Мы в дальнейшем будем изучать вынужденные квазиста- ционарные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону:

u = U_m sin ωt или u = U_m cos ωt,                     (2.4.2)

где U_m — амплитуда напряжения, а ω — циклическая частота колебаний. Когда колебания происходят длительное время, то значение начальной фазы не играет сколько-нибудь существенную роль. Поэтому начальную фазу можно принять равной нулю и с одинаковым успехом использовать как синусоидальную функцию, так и косинусоидальную.

Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Аналогично колебания скорости при вынужденных механических колебаниях не совпадают по фазе с колебаниями силы. Поэтому в общем случае

i = I_m sin (ωt + φ_с),                     (2.4.3)

где φ_с — разность (сдвиг) фаз между колебаниями силы тока и напряжения.

См. также

Фонд Викимедиа . 2010 .

Смотреть что такое “когерентные волны” в других словарях

когерентные волны – Волны, разность фаз которых не зависит от времени. Темы Виды (методы) и технология неразрушающего контроля … Руководство технического переводчика

когерентные волны – koherentinės bangos statusas T sritis fizika atitikmenys: angl. coherent waves vok. kohärente Wellen, f rus. coherent waves, f pranc. ondes cohérentes, f … Fizikos terminų žodynas

когерентные волны – (Когерентные волны) волны одинаковой частоты, колебания которых отличаются постоянной разностью фаз, не изменяющейся со временем … Русский указатель к Англо-русскому словарю музыкальной терминологии

когерентные световые волны – Световые волны с постоянной разностью фаз колебание света в течение определенного периода времени. Topics……… Руководство технического переводчика

WAVES – (1) (см.), распространяющийся с конечной скоростью в пространстве и несущий энергию, не неся материи; (2) проявление В. де Бройлем движения любой микрочастицы и отражающее одновременное сочетание волновых и корпускулярных свойств….. … Большая политехническая энциклопедия

электромагнитные волны – Электромагнитное поле, распространяющееся через пространство с конечной скоростью, которая зависит от свойств среды. В вакууме скорость электромагнитной волны составляет c≈300 000 км/с (см. скорость света). В однородных изотропных средах направления … … Энциклопедический словарь

Когерентность – (от лат. cohaerens – находящийся в общении) согласованное протекание во времени нескольких колебательных или волновых процессов, проявляющееся в их суммировании. Колебание называется когерентным, если его разность фаз остается постоянной…..

Помехи (физические) – Интерференционное изображение двух когерентных круговых волн в зависимости от длины волны и расстояния между источниками Интерференция волн – это суперпозиция волн, при которой происходит взаимное усиление в одних точках пространства и ослабление в других….. … Википедия

Интерференция волн – Это статья об интерференции в физике. См. также Интерференция и Интерференция света Интерференционное изображение большого числа когерентных круговых волн, зависящее от длины волны и расстояния между источниками Интерференция взаимных волн … Википедия

Интерференция (физика) – Это статья об интерференции в физике. См. также Интерференция (неоднозначность) и Интерференция света Интерференционное изображение двух когерентных волн с круговой формой, зависящей от длины волны и расстояния между источниками Интерференция волн – это нелинейное явление,… …Википедия

Волна от источника света расщепляется из-за преломления в двух половинках бипризмы. Результирующие волны 1 и 2 исходят от двух воображаемых источников S1 и S2 и являются когерентными, поэтому в заштрихованной области наблюдается интерференция..

Интерференция света в тонких пленках. Осветительная оптика.

Различные цвета тонких пленок обусловлены интерференцией двух волн, отраженных от нижней и верхней поверхностей пленки. При отражении от верхней поверхности пленки теряется половина волны.

Если параллельный пучок монохроматического излучения падает под определенным углом на тонкую плоскопараллельную пластину, то в отраженном свете пластина кажется светлой или темной.

Если пластина освещается белым светом, то выполняются условия максимума и минимума для отдельных длин волн, пластина становится цветной, а цвета в отраженном и проходящем свете дополняют друг друга до белого.

Когда монохроматический свет падает на пластину разной толщины, каждое значение l соответствует разным интерференционным условиям, так что пластину пересекают светлые и темные линии (полосы) – линии одинаковой толщины. Так, в клине это расположение параллельных линий (рис. 19.6), в воздушном зазоре между линзой и пластиной – кольца (кольца Ньютона).

При освещении пластины переменной толщины белым светом получаются разноцветные пятна и линии: цветные мыльные пленки, масляные и нефтяные пленки на поверхности воды, радужные цвета крыльев некоторых насекомых и птиц. В этих случаях полная прозрачность пленки не требуется.

Покрытие оптических поверхностей специальными пленками называется просветленной оптикой, а оптические системы с такими покрытиями называются просветленная оптика.

Покрыв поверхность стекла несколькими специально подобранными пленками, можно создать отражающий светофильтр, который пропускает или отражает излучение в определенном диапазоне длин волн путем интерференции.

· Использование бипризмы Френеля:

Что такое начальная фаза и как определить ее по графику колебаний

Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, \(\large \varphi_{0} \).

\(\large \varphi_{0} \left(\text{рад} \right) \) — начальная фаза, измеряется в радианах (или градусах).

Рис. 7. Угол отклонения качелей перед началом колебаний

Рассмотрим теперь, как величина \(\large \varphi_{0} \) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы \(\large \varphi_{0} \) принимаем равной нулю.

Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время \(\large \Delta t\), начальный угол \(\large \varphi_{0} \) будет отличаться от нулевого значения.

Определим угол \(\large \varphi_{0} \) с помощью графика колебаний.

Обратим внимание (рис. на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина \(\large \varphi_{0} \) — в радианах. Значит, нужно связать формулой кусочек времени \(\large \Delta t\) и соответствующий ему начальный угол \(\large \varphi_{0} \)

Значит, нужно связать формулой кусочек времени \(\large \Delta t\) и соответствующий ему начальный угол \(\large \varphi_{0} \).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

• Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал \(\large \Delta t\) равен 1 сек.
• Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.

Из графика следует, что период T = 4 сек.

Рассчитаем теперь, какую долю периода составляет интервал времени \(\large \Delta t\). Для этого составим такую дробь \(\large \displaystyle \frac{\Delta t }{T} \):

Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.

Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол \(\large 2\pi \). Найдем теперь, как связана найденная доля периода с углом \(\large 2\pi \) полного цикла.

Для этого используем формулу:

\(\large \displaystyle \frac{1}{4} \cdot 2\pi = \frac{\pi }{2} =\varphi_{0} \)

Значит, интервалу \(\large \Delta t\) соответствует угол \(\large \displaystyle \frac{\pi }{2} \) – это начальная фаза для красной кривой на рисунке.

В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса

То есть, кривая запаздывает относительно «чистого» синуса.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол \(\large \displaystyle \frac{\pi }{2} \) имеет знак «плюс».

Примечания:

1. Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
2. На графике колебаний начальная фаза \( \varphi_{0}\) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.

Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.

Генератор синусоидальных колебаний на основе моста Вина

Генератор синусоидальных колебаний на основе моста Вина или просто генератор Вина является одним из самых распространённых RC-генераторов синусоидальных колебаний. Схема данного генератора показана на рисунке ниже

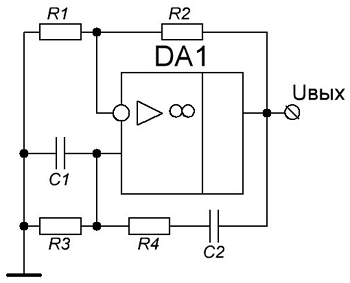
Схема генератора Вина на основе ОУ.

Генератор Вина состоит из ОУ DA1, который охвачен ООС (отрицательная обратная связь) посредством резисторов R1 и R2, а также ПОС (положительная обратная связь) с помощью частотно-избирательной цепи R3C1R4C2.

Частотно-избирательная цепь R3C1R4C2 называется мостом Вина, от названия которого и получил наименование генератор данного типа. Данный мост состоит из последовательно включённых дифференцирующей цепи R4C2 и интегрирующей цепи R3C1. Как известно для генерирования сигнала мост Вина должен обеспечить нулевой фазовый сдвиг сигнала. Это обеспечивается равенством постоянной времени интегрирующей цепи R3C1 и дифференцирующей цепи R4C2

Тогда частота, при которой будет сдвиг фаз равный нулю, определяется следующим выражением

При данном условии коэффициент передачи цепи ПОС будет равен 1/3. Поэтому для того чтобы компенсировать данное условие коэффициент передачи цепи ООС должен быть равен 3, то есть

Генератор с мостом Вина обеспечивает выходной синусоидальный сигнал с небольшими искажениями – порядка 0,05 %. Однако у данного типа генератора существует серьёзная проблема в том, что для получения качественного синусоидального сигнала необходимо обеспечить точные соотношения резисторов в цепи ООС R1 и R2, то есть обеспечить коэффициент передачи цепи равный трём (β = 1/3). Так если β < 1/3 то возникшие колебания будут с сильными искажениями, а в случае β > 1/3 даже если и возникнут колебания их амплитуда будет постепенно уменьшаться и со временем станет равной нулю. Поэтому для стабилизации работы генератора Вина применяют различные автоматические системы стабилизации амплитуды.

Большая энциклопедия нефти и газа.

Когерентные источники света можно получить, разделив пучок света, испускаемый каждым атомом одного источника, на две части и заставив эти две части перекрываться после прохождения путей разной длины. Тогда на каждое волнообразное цунами в одной части будет одно такое же цунами в другой части, и они смогут взаимопроникать друг в друга. Кроме того, разность путей не должна быть слишком большой (не более 1 м), чтобы каждая когерентная волна излучения из первой части могла встретить аналогичную когерентную волну из второй части и время их суперпозиции было достаточным для наблюдения интерференции.

Идеальный когерентный источник излучает свет ровно на одной частоте. Настоящий лазер излучает спектр колебаний – спектральную линию, в которой присутствуют несколько частот.

Источники когерентных колебаний могут быть реализованы, например, следующим образом: Возьмем точечный источник S (рис. 274), от которого распространяется сферическая волна. На пути волны находится барьер BB с двумя точечными отверстиями st и sa, расположенными симметрично относительно источника S. Согласно принципу Гюйгенса, отверстия s4 и sa становятся независимыми источниками колебаний, более того, они колеблются с одинаковой амплитудой и в одинаковых фазах, поскольку их расстояния от источника S одинаковы.

Источники когерентного белого света, расположенные на расстоянии 0 32 мм друг от друга, имеют форму узких щелей. Экран, на котором наблюдается интерференция света от этих источников, находится на расстоянии 3 2 м.

Когерентные источники белого света, расстояние между которыми составляет 0 32 мм, имеют форму узких щелей. Экран, на котором наблюдается интерференция света от этих источников, находится на расстоянии 3 2 м от них.

Когерентные источники белого света, расстояние между которыми составляет 0 32 мм, имеют форму узких щелей. Экран, на котором мы наблюдаем интерференцию света от этих источников, находится на расстоянии 3 2 м от них.

Когерентные источники белого света, расстояние между которыми составляет 0 32 мм, имеют форму узких щелей. Экран, на котором мы наблюдаем интерференцию света от этих источников, находится на расстоянии 3 2 м от них.

Когерентные источники белого света на расстоянии 0 32 мм выглядят как узкие щели. Экран, на котором наблюдается интерференция света от этих источников, находится на расстоянии 3 2 м.

Когерентные источники белого света, расстояние между которыми составляет 0 32 мм, имеют форму узких щелей. Экран, на котором наблюдается интерференция света от этих источников, находится на расстоянии 3 2 м от них.

Читайте далее:

• Урок 7 Свободные и вынужденные электромагнитные колебания. колебательный контур – физика – 11 класс – Русская электронная школа.
• Затухающие колебания – это. Что такое затухающие колебания?.
• Значение слова «амплитуда» в 11 словарях.
• Механические колебания и волны; FIZI4KA.
• 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
• Видимый диапазон.
• Уравнения электромагнитных волн в физике.

Максимальная кинетическая энергия груза на пружине

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .

При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.

Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.

Для груза на пружине:

Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .

Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени

Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия

Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.

Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

1) амплитуда колебаний скорости

2) циклическая частота колебаний

3) максимальная кинетическая энергия груза

4) период колебаний

А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле

Б) Для пружинного маятника известны формулы кинетической энергии

Пру­жин­ный ма­ят­ник, со­сто­я­щий из груза и лёгкой пру­жи­ны, со­вер­ша­ет ко­ле­ба­ния. В мо­мент, когда груз на­хо­дит­ся в край­нем по­ло­же­нии, его не­мно­го под­тал­ки­ва­ют вдоль оси пру­жи­ны в на­прав­ле­нии от по­ло­же­ния

рав­но­ве­сия. Как в ре­зуль­та­те этого из­ме­ня­ют­ся мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка и ча­сто­та его ко­ле­ба­ний?

Для каж­дой ве­ли­чи­ны опре­де­ли­те со­от­вет­ству­ю­щий ха­рак­тер из­ме­не­ния:

3) не из­ме­ня­ет­ся

За­пи­ши­те в таб­ли­цу вы­бран­ные цифры для каж­дой фи­зи­че­ской ве­ли­чи­ны. Цифры в от­ве­те могут по­вто­рять­ся.

Мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка

Ча­сто­та ко­ле­ба­ний ма­ят­ни­ка

Груз под­толк­ну­ли от по­ло­же­ния рав­но­ве­сия, от­ку­да сле­ду­ет, что ам­пли­ту­да ко­ле­ба­ний груза уве­ли­чит­ся. При этом уве­ли­чит­ся также и мак­си­маль­ная по­тен­ци­аль­ная энер­гия пру­жи­ны. По за­ко­ну со­хра­не­ния энер­гии, это при­ве­дет к уве­ли­че­нию мак­си­маль­ной ки­не­ти­че­ской энер­гии груза ма­ят­ни­ка.

Пе­ри­од и ча­сто­та пру­жин­но­го ма­ят­ни­ка за­ви­сят толь­ко от массы груза и жест­ко­сти пру­жи­ны. Таким об­ра­зом, при уве­ли­че­нии ам­пли­ту­ды ко­ле­ба­ний груза, ча­сто­та ко­ле­ба­ний ма­ят­ни­ка не из­ме­нит­ся.