Закон ома для полной и не полной эллектрической цепи, формула и правильное определение

Физика

Коэффициент полезного действия источника тока ( КПД ) определяется долей полезной мощности от полной мощности источника тока:

η = P полезн P полн ⋅ 100 % ,

где P полезн — полезная мощность источника тока (мощность, выделяющаяся во внешней цепи); P полн — полная мощность источника тока:

P полн = P полезн + P потерь ,

т.е. суммарная мощность, выделяющаяся во внешней цепи ( P полезн ) и в источнике тока ( P потерь ).

Коэффициент полезного действия источника тока (КПД) определяется долей полезной энергии от полной энергии, вырабатываемой источником тока:

η = E полезн E полн ⋅ 100 % ,

где E полезн — полезная энергия источника тока (энергия, выделяющаяся во внешней цепи); E полн — полная энергия источника тока:

E полн = E полезн + E потерь ,

т.е. суммарная энергия, выделяющаяся во внешней цепи ( E полезн ) и в источнике тока ( E потерь ).

Энергия источника тока связана с мощностью источника тока следующими формулами:

энергия, выделяющаяся во внешней цепи (полезная энергия) за время t , связана с полезной мощностью источника P полезн —

E полезн = P полезн t ;

энергия, выделяющаяся в источнике тока (энергия потерь) за время t , связана с мощностью потерь источника P потерь —

E потерь = P потерь t ;

полная энергия , вырабатываемая источником тока за время t , связана с полной мощностью источника P полн —

E полн = P полн t .

Коэффициент полезного действия источника тока (КПД) может определяться:

долей, которую составляет сопротивление внешней цепи от суммарного сопротивления источника тока и нагрузки (внешней цепи), —

где R — сопротивление цепи (нагрузки), к которой подключен источник тока; r — внутреннее сопротивление источника тока;

долей, которую составляет разность потенциалов на клеммах источника от его электродвижущей силы, —

где U — напряжение на зажимах (клеммах) источника тока; ℰ — ЭДС источника тока.

При максимальной мощности , выделяющейся во внешней цепи, КПД источника тока равен 50 %:

так как в этом случае сопротивление нагрузки R равно внутреннему сопротивлению r источника тока:

η * = R R + r ⋅ 100 % = r r + r ⋅ 100 % = r 2 r ⋅ 100 % = 50 % .

Пример 16. При подключении источника тока с КПД 75 % к некоторой цепи на ней выделяется мощность, равная 20 Вт. Найти количество теплоты, выделившееся в источнике тока за 10 мин.

Решение . Проанализируем условие задачи.

Мощность, выделяющаяся во внешней цепи, является полезной:

P полезн = 20 Вт,

где P полезн — полезная мощность источника тока.

Количество теплоты, которое выделяется в источнике тока, связано с мощностью потерь:

Q потерь = P потерь t ,

где P потерь — мощность потерь; t — время работы источника тока.

КПД источника связывает полезную и полную мощности:

η = P полезн P полн ⋅ 100 % ,

где P полн — полная мощность источника тока.

Полезная мощность и мощность потерь в сумме дают полную мощность источника тока:

P полн = P полезн + P потерь .

Записанные уравнения образуют систему уравнений:

η = P полезн P полн ⋅ 100 % , Q потерь = P потерь t , P полн = P полезн + P потерь . >

Для нахождения искомой величины — количества теплоты, выделившейся в источнике Q потерь , — необходимо определить мощность потерь P потерь . Выполним подстановку третьего уравнения в первое:

η = P полезн P полезн + P потерь ⋅ 100 %

и выразим P потерь :

P потерь = 100 % − η η P полезн .

Подставим полученную формулу в выражение для Q потерь :

Q потерь = 100 % − η η P полезн t .

Q потерь = 100 % − 75 % 75 % ⋅ 20 ⋅ 10 ⋅ 60 = 4,0 ⋅ 10 3 Дж = 4,0 кДж .

За указанное в условии задачи время в источнике выделится 4,0 кДж теплоты.

Источник

Формулировка закона Ома следующая:

Величина силы тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению.

Эту зависимость можно выразить формулой:

Где I – сила тока, U – напряжение, приложенное к участку цепи, а R – электрическое сопротивление участка цепи.Так, если известны две из этих величин можно легко вычислить третью.Понять закон Ома можно на простом примере. Допустим, нам необходимо вычислить сопротивление нити накаливания лампочки фонарике и нам известны величины напряжения работы лампочки и сила тока, необходимая для ее работы (сама лампочка, чтобы вы знали имеет переменное сопротивление, но для примера примем его как постоянное). Для вычисления сопротивления необходимо величину напряжения разделить на величину силы тока. Как же запомнить формулу закона Ома, чтобы правильно провести вычисления? А сделать это очень просто! Вам нужно всего лишь сделать себе напоминалку как на указанном ниже рисунке.Теперь закрыв рукой любую из величин вы сразу поймете, как ее найти. Если закрыть букву I, становится ясно, что чтобы найти силу тока нужно напряжение разделить на сопротивление.Теперь давайте разберемся, что значат в формулировке закона слова « прямо пропорциональна и обратно пропорциональна. Выражение «величина силы тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку» означает, что если на участке цепи увеличится напряжение, то и сила тока на данном участке также увеличится. Простыми словами, чем больше напряжение, тем больше ток. И выражение «обратно пропорциональна его сопротивлению» значит, что чем больше сопротивление, тем меньше будет сила тока.Рассмотрим пример с работой лампочки в фонарике. Допустим, что для работы фонарика нужны три батарейки, как показано на схеме ниже, где GB1 – GB3 – батарейки, S1 – выключатель, HL1 – лампочка.

Примем, что сопротивление лампочки условно постоянно, хотя нагреваясь её сопротивление увеличивается. Яркость лампочки будет зависеть от силы тока, чем она больше, тем ярче горит лампочка. А теперь, представьте, что вместо одной батарейки мы вставили перемычку, уменьшив тем самым напряжение.Что случится с лампочкой?Она будет светить более тускло (сила тока уменьшилась), что подтверждает закон Ома:чем меньше напряжение, тем меньше сила тока.

Вот так просто работает этот физический закон, с которым мы сталкиваемся в повседневной жизни.Бонус специально для вас шуточная картинка не менее красочно объясняющая закон Ома.

Закон Ома, в отличие от, например, закона Кулона, это не фундаментальный закон физики. Он имеет практическое значение.В природе существуют вещества, проводящие электрический ток – проводники и не проводящие – диэлектрики.В проводниках есть свободные заряды – электроны. Для того, чтобы электроны начали дружно перемещаться в одном направлении, необходимо электрическое поле, которое и «заставит» их перемещаться от одного конца проводника к другому.Простейшим образом создать поле может обыкновенная батарейка. Если на конце проводника недостаток электронов, то он знаком «+», если , то «-». Электроны, имеющие всегда отрицательный заряд, естественно, устремятся к плюсу. Так в проводнике рождается электрический ток, т. е. направленное перемещение электрических зарядов. Чтобы его увеличить, необходимо усилить электрическое поле в проводнике. Или, как говорят, приложить к концам проводника большее напряжение.Электрический ток принято обозначать буквой I, а напряжение – буквой U.

Но проводники, по которым перемещаются свободные электроны, могут иметь разное электрическое сопротивление R. Сопротивление показывает меру противодействия материала проводника прохождения по нему электрического тока. Оно зависит только от геометрических размеров, материала проводника и его температуры.Каждая из этих величин имеет свои единицы измерения: Сила тока I измеряется в Амперах (А); Напряжение U измеряется в Вольтах (В); Сопротивление измеряется в Омах (Ом).

Немного о сопротивлении

Использование электрического тока, бесспорно, вывело научно-технический прогресс на новую ступень, дало ему гигантский толчок. Но сила сопротивления протеканию тока становится на пути такого развития.

С одной стороны, электрический ток обладает бесценными свойствами, используемыми в быту и технике, с другой – имеется значительное противодействие. Физика как наука о природе пытается установить баланс, привести в соответствие эти обстоятельства.

Сопротивление тока возникает вследствие взаимодействия электрически заряженных частиц с веществом, по которому они движутся. Исключить этот процесс в нормальных температурных условиях невозможно.

Влияние внутреннего сопротивления на свойства двухполюсника

Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.

Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:

ЭДС генератора напряжения U
Внутреннее сопротивление r

В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов U out = φ 2 − φ 1

) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

(Напряжения)

где U out1I 1 ,U out2 — выходное напряжение при токеI 2 . Решая систему уравнений, находим искомые неизвестные:

Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система () записывается следующим образом:

где U oc

— выходное напряжение в режиме холостого хода (англ.open circuit ), то есть при нулевом токе нагрузки;I sc — ток нагрузки в режиме короткого замыкания (англ.short circuit ), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

(ВнутрСопр)

Измерение

Понятие измерение

применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение , которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.

Иногда применяется следующий простой способ измерения, не требующий вычислений:

Измеряется напряжение холостого хода
В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.

Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.

Реактивное внутреннее сопротивление

Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности , то расчет

реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды , то есть расчет производится методом комплексных амплитуд .

Измерение

реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией , а не скалярным значением:

Можно искать различные параметры комплексного значения: модуль , аргумент , только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путем измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения навсех частотах, которые может генерировать источник данного двухполюсника.

Говорим о напряжении

Не менее важно понять что такое напряжение. Давайте сразу начнем с аналогии и снова используем воду

Пусть в воронке находится вода. Она просачивается через узкое горлышко, которое создает сопротивление. Если представить, что на воду уложили груз, движение воды ускорится. Этот груз — и есть напряжение. И теперь тоже понятно, почему чем выше напряжение, тем сильнее ток — чем сильнее давление, тем быстрее будет двигаться вода. То есть, зависимость прямая: больше напряжение — больше ток. И именно это положение отражает закон Ома — «давление» стоит в числителе (в верхней части дроби).

Можно попробовать представить напряжение по-другому. Есть все те же электроны, которые скопились на одном краю источника питания. На втором краю их мало. Так как каждый из электронов имеет какой-то заряд, там, где их много, суммарный заряд больше, где мало — меньше. Разница между зарядами и есть напряжение. Это тоже несложно представить. С точки зрения электричества — это более корректное представление, хоть и не точное.

На тему закона Ома есть немало забавных картинок, позволяющих чуть лучше понять все эти явления. Одна из них перед вами и иллюстрирует, как ток зависит от напряжения и сопротивления. Смотрите что получается: сопротивление старается уменьшить ток (обратная зависимость), а с ростом напряжения он увеличивается (прямая зависимость). Это и есть закон Ома, но переданный простыми словами.

Благодаря картинке просто понять зависимость тока от напряжения и сопротивления

Если вы хотите убедиться и в этой зависимости, тоже надо создать простенькую цепь. Но нужен будет либо регулируемый источник питания, либо несколько батареек, которые выдают разное напряжение. Или можно последовательно включать несколько батареек — тоже вариант. Но менять/подпаивать батарейки надо при разорванной цепи (выключенном тумблере).

В этой схеме используются два измерительных прибора: амперметр включается последовательно с нагрузкой (резистор на схеме ниже), вольтметр параллельно нагрузке.

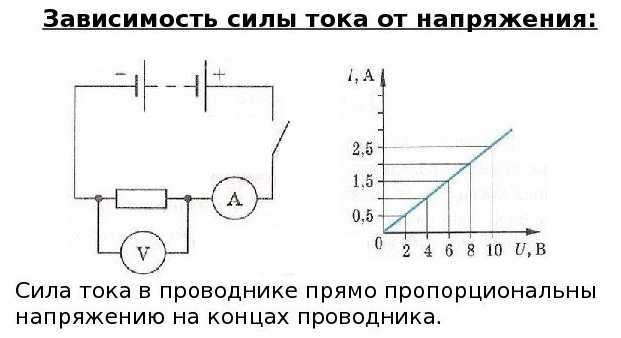
Схема для иллюстрации закона Ома

Так как другие параметры цепи остаются в норме, при увеличении напряжения мы увидим увеличение силы тока. Чем больше напряжение подаем, тем больше отклоняются стрелки вольтметра и амперметра. Если задаться целью построить график, он будет в виде прямой. Если поставить другое сопротивление, график также будет в виде прямой, но угол наклона ее изменится.

Практическое использование

Собственно, к любому участку цепи можно применить этот закон. Пример приведен на рисунке.

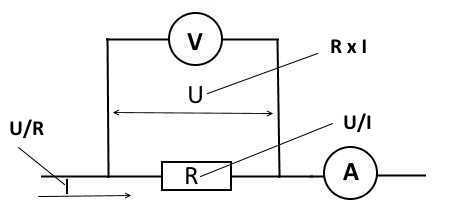Применяем закон к любому участку цепи.

Используя такой план, можно вычислить все необходимые характеристики для неразветвленного участка. Рассмотрим более детальные примеры.

Находим силу тока

Рассмотрим теперь более определенный пример, допустим, возникла необходимость узнать ток, протекающий через лампу накаливания. Условия:

Напряжение – 220 В;
R нити накала – 500 Ом.

Решение задачи будет выглядеть следующим образом: 220В/500Ом=0,44 А.

Рассмотрим еще одну задачу со следующими условиями:

R=0,2 МОм;
U=400 В.

В этом случае, в первую очередь, потребуется выполнить преобразование: 0,2 МОм = 200000 Ом,после чего можно приступать к решению: 400 В/200000 Ом=0,002 А (2 мА). Вычисление напряжения Для решения мы также воспользуемся законом, составленным Омом. Итак задача:

R=20 кОм;
I=10 мА.

Преобразуем исходные данные:

20 кОм = 20000 Ом;
10 мА=0,01 А.

Решение: 20000 Ом х 0,01 А = 200 В.

Незабываем преобразовывать значения, поскольку довольно часто ток может быть указан в миллиамперах.

Сопротивление

Несмотря на то, что общий вид способа для расчета параметра «R» напоминает нахождение значения «I», между этими вариантами существуют принципиальные различия. Если ток может меняться в зависимости от двух других параметров, то R (на практике) имеет постоянное значение. То есть по своей сути оно представляется в виде неизменной константы.

Если через два разных участка проходит одинаковый ток (I), в то время как приложенное напряжение (U) различается, то, опираясь на рассматриваемый нами закон, можно с уверенностью сказать, что там где низкое напряжение «R» будет наименьшим. Рассмотрим случай когда разные токи и одинаковое напряжение на несвязанных между собой участках. Согласно закону, составленному Омом, большая сила тока будет характерна небольшому параметру «R».

Рассмотрим несколько примеров

Допустим, имеется цепь, к которой подведено напряжение U=50 В, а потребляемый ток I=100 мА. Чтобы найти недостающий параметр, следует 50 В / 0,1 А (100 мА), в итоге решением будет – 500 Ом.

Вольтамперная характеристика позволяет наглядно продемонстрировать пропорциональную (линейную) зависимость закона. На рисунке ниже составлен график для участка с сопротивлением равным одному Ому (почти как математическое представление закона Ома).

Изображение вольт-амперной характеристики, где R=1 Ом

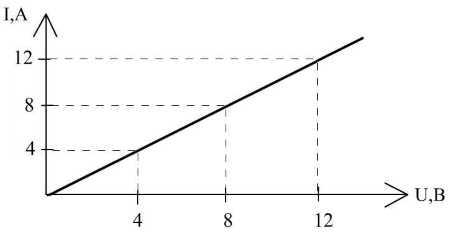Изображение вольт-амперной характеристики

Вертикальная ось графика отображает ток I (A), горизонтальная – напряжение U(В). Сам график представлен в виде прямой линии, которая наглядно отображает зависимость от сопротивления, которое остается неизменным. Например, при 12 В и 12 А «R» будет равно одному Ому (12 В/12 А).

Обратите внимание, что на приведенной вольтамперной характеристике отображены только положительные значения. Это указывает, что цепь рассчитана на протекание тока в одном направлении

Там где допускается обратное направление, график будет продолжен на отрицательные значения.

Заметим, что оборудование, вольт-амперная характеристика которого отображена в виде прямой линии, именуется — линейным. Этот же термин используется для обозначения и других параметров.

Помимо линейного оборудования, есть различные приборы, параметр «R» которых может меняться в зависимости от силы тока или приложенного напряжения. В этом случая для расчета зависимости нельзя использовать закон Ома. Оборудование такого типа называется нелинейным, соответственно, его вольт-амперные характеристики не будут отображены в виде прямых линий.

Для переменного тока

В цепи переменного тока закон Ома может иметь некоторые особенности, описанные ниже.

Импеданс, Z

В цепи переменного тока, сопротивление кроме активной (R), может иметь как емкостную (C), так и индуктивную (L) составляющие. В этом случае вводится понятие электрического импеданса, Z (полного или комплексного сопротивления для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих.

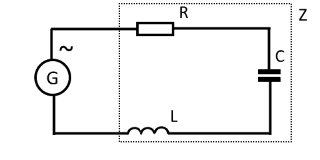Последовательное включение R, L, C

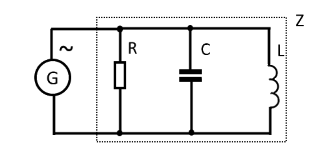Параллельное включение R, L, C

Также, полное сопротивление, Z зависит не только от емкостной (C), индуктивной (L) и активной (R) составляющих, но и от частоты переменного тока.

Импеданс, Полное сопротивление, Z
При последовательном включении R, L, C	При параллельном включении R, L, C
Z=√(R2+(ωL-1/ωC)2)	Z=1/ √(1/R2+(1/ωL-ωC)2)
где,
ω = 2πγ — циклическая, угловая частота; γ — частота переменного тока.

Коэффициент мощности, Cos(φ)

Коэффициент мощности, в самом простом понимании, это отношение активной мощности (P) потребителя электрической энергии к полной (S) потребляемой мощности, т. е.

Cos(φ) = P / S

Он также показывает насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.Изменяется от 0 до 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), то коэффициент мощности равен единице.Чем ближе Cos(φ) к единице, тем меньше потерь энергии в электрической цепи.

Исходя из вышеперечисленных понятий импеданса Z и коэффициента мощности Cos(φ), характерных для переменного тока, выведем формулу закона Ома, коэффициента мощности и их производные для цепей переменного тока:

I = U / Z	где	I — сила переменного тока, измеряемая в Амперах, (A)
U — напряжение переменного тока, измеряемое в Вольтах, (V)
Z — полное сопротивление (импеданс), измеряется в Омах, (Ω)

Производные формулы:

Сила тока,	I=	U/Z	P/(U×Cos(φ))	√(P/Z)
Напряжение,	U=	I×Z	P/(I×Cos(φ))	√(P×Z)
Полное сопротивление, импеданс	Z=	U/I	P/I²	U²/P
Мощность,	P=	I²×Z	I×U×Cos(φ)	U²/Z

Программа «КИП и А» имеет в своем составе блок расчета закона Ома как для постоянного и переменного тока, так и для расчета импеданса и коэффициента мощности Cos(φ). Скриншоты представлены на рисунках внизу:

Закон Ома для постоянного тока

Закон Ома для переменного тока

Расчет полного сопротивления

Расчет коэффициента мощности Cos(φ)

Закон Ома для полной цепи

Подробности: Просмотров: 453

«Физика — 10 класс»

Сформулируйте закон Ома для участка цепи.Из каких элементов состоит электрическая цепь?Для чего служит источник тока?

Рассмотрим простейшую полную (т. е. замкнутую) цепь, состоящую из источника тока (гальванического элемента, аккумулятора или генератора) и резистора сопротивлением R (рис. 15.10). Источник тока имеет ЭДС Ε и сопротивление r.

В генераторе r — это сопротивление обмоток, а в гальваническом элементе сопротивление раствора электролита и электродов.

Сопротивление источника называют внутренним сопротивлением в отличие от внешнего сопротивления R цепи.

Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление цепи R + r. Эта связь может быть установлена теоретически, если использовать закон сохранения энергии и закон Джоуля—Ленца (15.14).

Пусть за время Δt через поперечное сечение проводника проходит электрический заряд Δq. Тогда работу сторонних сил при перемещении заряда Δq можно записать так: А_ст = ΕΔq. Согласно определению силы тока (15.1) Δq = IΔt. Поэтому

А_ст = ΕIΔt. (15.17)

При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых г и Я, выделяется некоторое количество теплоты. По закону Джоуля—Ленца оно равно:

Q = I2RΔt + I2rΔt. (15.18)

По закону сохранения энергии А_ст = Q, откуда получаем

Ε = IR + 1r. (15.19)

Произведение силы тока и сопротивления участка цепи называют падением напряжения на этом участке.

Таким образом, ЭДС равна сумме падений напряжения на внутреннем и внешнем участках замкнутой цепи.

Закон Ома для замкнутой цепи:

Сила тока в замкнутой цепи равна отношению ЭДС источника тока к полному сопротивлению цепи.

Согласно этому закону сила тока в цепи зависит от трёх величин: ЭДС Ε сопротивлений R внешнего и г внутреннего участков цепи. Внутреннее сопротивление источника тока не оказывает заметного влияния на силу тока, если оно мало по сравнению с сопротивлением внешней части цепи (R >> r). При этом напряжение на зажимах источника примерно равно ЭДС: U = IR = Ε — Ir ≈ Ε

При коротком замыкании, когда R ≈ 0, сила тока в цепи и определяется именно внутренним сопротивлением источника и при электродвижущей силе в несколько вольт может оказаться очень большой, если r мало (например, у аккумулятора r ≈ 0,1 — 0,001 Ом). Провода могут расплавиться, а сам источник выйти из строя.

Если цепь содержит несколько последовательно соединённых элементов с ЭДС Ε₁, Ε₂, Ε₃ и т. д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных элементов.

Для определения знака ЭДС любого источника нужно вначале условиться относительно выбора положительного направления обхода контура. На рисунке (15.11) положительным (произвольно) считают направление обхода против часовой стрелки.

Если при обходе цепи данный источник стремится вызвать ток в направлении обхода, то его ЭДС считается положительной: Ε > 0. Сторонние силы внутри источника совершают при этом положительную работу.

Если же при обходе цепи данный источник вызывает ток против направления обхода цепи, то его ЭДС будет отрицательной: Ε < 0. Сторонние силы внутри источника совершают отрицательную работу. Так, для цепи, изображённой на рисунке 15.11, при обходе контура против часовой стрелки получаем следующее уравнение:

Ε_п = Ε₁ + Ε₂ + Ε₃ = lΕ₁| — |Ε₂| + |Ε₃|

Если Ε_п > 0, то согласно формуле (15.20) сила тока I > 0, т. е. направление тока совпадает с выбранным направлением обхода контура. При Ε_п < 0, наоборот, направление тока противоположно выбранному направлению обхода контура. Полное сопротивление цепи R_п равно сумме всех сопротивлений (см. рис. 15.11):

R_п = R + r₁ + r₂ + r₃.

Для любого замкнутого участка цепи, содержащего несколько источников токов, справедливо следующее правило: алгебраическая сумма падений напряжения равна алгебраической сумме ЭДС на этом участке (второе правило Кирхгофа):

I₁R₁+ I₂R₂ + … + I_nR_n = Ε₁ + Ε₂ + … + Ε_m

Следующая страница «Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»»

Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»

Законы постоянного тока — Физика, учебник для 10 класса — Класс!ная физика

Электрический ток. Сила тока — Закон Ома для участка цепи. Сопротивление — Электрические цепи. Последовательное и параллельное соединения проводников — Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» — Работа и мощность постоянного тока — Электродвижущая сила — Закон Ома для полной цепи — Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»

Короткое замыкание

С уменьшением сопротивления внешней цепи, R -> 0, сила тока достигает максимального значения I_к.з. Этот случай называют коротким замыканием. Для источников тока, имеющих сравнительно малое внутреннее сопротивление (например, в свинцовых аккумуляторах r=0,1-0,001 Ом), сила тока короткого замыкания может достичь очень больших значений. Проводники могут расплавиться, а сам источник — выйти из строя. Особенно опасны короткие замыкания в осветительных сетях, питающихся от трансформаторных подстанций, ЭДС которых измеряется сотнями вольт. Сила тока короткого замыкания в них может достичь нескольких тысяч ампер.